We are going to learn the Counting principle with the Permutation and Combination class 11. This chapter is not about calculations, it’s totally based on analytical thinking and reasoning ability. These concepts are the foundation of Probability.
Introduction
The permutation means ‘ordered selection’. It can be defined as the number of ways ‘r’ things can be selected and arranged, from amongst ‘n’ different things, at a time.
Here nPr represents the possible number of ways r things can be selected and arranged, from n different things. (n\geq r)
nPr =\frac{n!}{(n-r!)}
n!=n×(n-1)×(n-2)×(n-3)×………×3×2×1

The Combination deals with the possible number of ways ‘r’ things can be selected out of ‘n’ different things. Here the order is not important. It is represented by nCr.
nCr =\frac{n!}{r!\times (n-r)!}
nPr =r!×nCr
Real-life examples of Permutation and Combination
Permutations deal with the arrangement of items so the Order of things is important.
Example: The combination lock can’t be unlocked until the right sequence of digits or alphabets (Password) is not entered.

In Combination, Order of the things is not important. Like the selection of 11 team members out of 20.
Difference between permutation and Combination Class 11
How many arrangements/groups of two letters can be formed using the letters A, B, and C? (Permutation and Combination class 11)
- Arrangements mean Permutations.
- Groups mean Combinations.

| Permutation | Combination |
| For each Combination, there are multiple Permutations possible. | For each Permutation, there is only one Combination possible. |
| Ordered Elements. | The order of elements is not important. |
| The Permutations of two letters from three given letters A, B and C are AB, BA, BC, CB, AC, and CA. | The combinations of two letters from three given letters A, B, and C are AB, BC, and AC. |
| The permutation is the superset of the Combination. | The combination is the subset of the permutation. |
NCR formulas
1) nC0 +nC1 +nC2 +…………+nCn= 2n
Proof: Binomial Theorem for positive integer n
(a+b)n=nC0.an +nC1.an-1.b +nC2.an-2.b2 +nC3.an-3.b3 +………+nCn-1.a.bn-1 +nCn.bn
Put a=b=1
nC0 +nC1 +nC2 +…………+nCn= 2n
2) nC0 –nC1 +nC2 -…………+(-1)n.nCn= 0
Proof: Binomial Theorem for positive integer n
(a-b)n=nC0.an +nC1.an-1.(-b) +nC2.an-2.(-b)2 +nC3.an-3.b3 +………+nCn-1.a.(-b)n-1 +nCn.(-b)n
Put a=b=1 (Permutation and Combination class 11)
nC0 –nC1 +nC2 -…………+(-1)n.nCn= 0
3) nCr +nCr-1 =n+1Cr
4) If nCx =nCy then x=y or x+y=n
5) nCr= nCn-r
6) r.nCr =n.n-1Cr-1
7) For nCr to be the greatest (Permutation and Combination class 11)
- If n is even, r=\frac{n}{2}.
- If n is odd, r=\frac{n+1}{2} or r=\frac{n-1}{2}.
8) \frac{^{n}C_{r}}{r+1}=\frac{^{n+1}C_{r+1}}{n+1}.
9) ^nC_0+\frac{^nC_1}{2}+\frac{^nC_2}{3}+\frac{^nC_3}{4}+.........+\frac{^nC_n}{n+1}=\frac{2^{n+1}-1}{n+1}.
Proof: \sum\limits_{r=0}^{n}\frac{^nC_r}{r+1}.
⇒\sum\limits_{r=0}^{n}\frac{^nC_r}{r+1}\times \frac{n+1}{n+1}.
⇒\frac{1}{n+1}\times\sum\limits_{r=0}^{n}\frac{n+1}{r+1}.^nC_r.
According to the Previous formula: \frac{n+1}{r+1}.^nC_r=^{n+1}C_{r+1}.
⇒\frac{1}{n+1}\times\sum\limits_{r=0}^{n}.^{n+1}C_{r+1}.
⇒ \frac{1}{n+1}\times(^{n+1}C_1+^{n+1}C_2+^{n+1}C_3+^{n+1}C_4+........+^{n+1}C_{n+1}).
⇒ \frac{1}{n+1}\times(2^{n+1}-^{n+1}C_0).
⇒ \frac{1}{n+1}\times(2^{n+1}-1)…….. Hence proved

Counting Principle
Before using formulas we have to know the concept behind these formulas which is known as the Counting Principle.
Consider choice A has ‘m’ options and choice B has ‘n’ options. Now the total number of ways to choose one option from A and then one option from B would be m×n.
Arrangement of digits
Some Permutations and Combinations Examples…
Que 1: How many three-digit numbers can be formed with the digit 1,2,3,4,5?
Case 1: The repetition of digits is allowed. (Permutation and Combination class 11)
Here we have three vacant places, where digits have to be placed according to given conditions.
Hundreds place: 5 choices
Tens place: 5 choices
Unit place: 5 choices
Total possible numbers (arrangements)= 5×5×5= 125
Case 2: The repetition of digits is not allowed.
Hundreds place: 5 choices
Tens place: 4 choices (One digit is already in use)
Unit place: 3 choices (Two digits are already in use)
Total possible numbers (arrangements)= 5×4×3= 60
Que 2: How many three-digit numbers can be formed with the digit 0,1,2,3,4?
Case 1: The repetition of digits is allowed. (Permutation and Combination class 11)
Hundreds place: 4 choices (0 can’t be used)
Tens place: 5 choices
Unit place: 5 choices
Total possible numbers (arrangements)= 4×5×5= 100
Case 2: The repetition of digits is not allowed.
Hundreds place: 4 choices (0 can’t be used)
Tens place: 4 choices
Unit place: 3 choices
Total possible numbers (arrangements)= 4×4×3= 48
Que 3: How many three-digit ‘Even Numbers’ can be formed with the digit 0,1,2,3,4,5?
Here, only 0,2 and 4 can be used at the unit place.
Case 1: The repetition of digits is allowed. (Permutation and Combination class 11)
Hundreds place: 5 choices (0 can’t be used)
Tens place: 6 choices
Unit place: 3 choices (Only 0,2 & 4 can be used)
Total possible numbers (arrangements)= 5×6×3= 90
Case 2: The repetition of digits is not allowed.
Step 1: When the unit digit is zero.
Unit place: 1 choice (Only Zero)
Hundreds place: 5 choices
Tens place: 4 choices
Possible arrangements= 1×5×4= 20
Step 2: When zero is not at the unit’s place.
Unit place: 2 choices (2 & 4)
Hundreds place: 4 choices (0 can’t be used and one digit is already in use)
Tens place: 4 choices (Two digits are already in use)
Possible arrangements= 2×4×4= 32
Total possible numbers (arrangements)= 20 + 32= 52
Que 4: How many numbers between 1800 and 4600 can be formed with the digits 0,1,2,3,4,5,6 and 7 if repetition is not allowed?
Solution: First, we have to find such numbers between 2000 to 5000.
It’s a four-digit Number = _ _ _ _ (Permutation and Combination class 11)
Thousands place: 3 choices (2,3,4)
Hundreds place: 7 choices (One digit is already in use)
Tens place: 6 choices (Two digits are already in use)
Unit place: 5 choices (Three digits are already in use)
Possible arrangements=3×7×6×5 =630 ……….(i)
* Numbers between 1800 to 2000:
No such number can be formed because 8 and 9 are unavailable for Hundreds place.
* Numbers between 4600 to 5000:
Thousands place: 1 choice (Only 4)
Hundreds place: 2 choices (6 or 7)
Tens place: 6 choices (Two digits are already in use)
Unit place: 5 choices (Three digits are already in use)
Possible arrangements=1×2×6×5 =60 ……….(ii)
Final result= 630-60= 570
Que 5: How many three-digit numbers can be formed from the digits 0, 1, 2, 3, and 5 which are divisible by 3? (Permutation and Combination Class 11)
Solution: If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.
Required Pairs= {(0,1,2), (0,1,5), (1,2,3), (1,3,5)}
(0,1,2)⇒ Total Numbers with these digits= 2×2×1=4
(0,1,5)⇒ Total Numbers with these digits= 2×2×1=4
(1,2,3)⇒ Total Numbers with these digits= 3×2×1=6
(1,3,5)⇒ Total Numbers with these digits= 3×2×1=6
Required three-digit numbers= 4+4+6+6= 20
Que 6: Find the sum of the four-digit numbers formed from the digits 1, 2, 5, and 7 if repetition of the digits is not allowed. (Permutation and Combination Class 11)
Solution: Possible arrangements= 4×3×2×1=24
\frac{24}{4}=6……..(i)
This means that while adding all the numbers, each digit repeats 6 times at the ones, tens, hundreds, and thousandths places.
The sum of all the digits in the ones, tens, hundreds, or thousandths place= 6×(1+2+5+7)= 90
Sum of all the numbers= 90×1000+90×100+90×10+90 =99990
Que 7: Find the sum of the four-digit numbers formed from the digits 0, 1, 2, 3, and 4 if repetition of the digits is not allowed. (Permutation and Combination Class 11)
Solution: Number of possible arrangements= 4×4×3×2=96
At the thousandth place, every number except 0 will be repeated 24 times (96/4=24).
Sum of all the digits in the thousandth place = 24×(1+2+3+4)= 240 …………(i)
If any number except 0 is at the unit place then possible arrangements= 3×3×2×1= 18
This means that this pair of 18 repeats 4 times and in the remaining 24 positions 0 is at the unit place.
Sum of all the digits in the unit place = 24×0+ 18×(1+2+3+4)= 180 …………(ii)
Similarly,
Sum of all the digits in the tens place = 24×0+ 18×(1+2+3+4)= 180 …………(iii)
Sum of all the digits in the hundreds place = 24×0+ 18×(1+2+3+4)= 180 ………(iv)
Sum of all 96 numbers= (240×1000)+(180×100)+(180×10)+(180×1)
=259,980
Que 8: How many five-digit numbers can be formed from the digits 1, 2, 3, 4, and 5 such that the odd numbers do not occupy the odd places?
Solution: Odd × Even × Odd × Even × Odd
Note: Only even numbers (2) can occupy odd positions (Permutation and Combination Class 11)
Total numbers= 2×5×2×5×2= 200
Que 9: How many four-digit numbers can be formed from the digits 0, 1, 3, 5, and 8 such that all numbers are divisible by 5?
Solution: Only 0 and 5 can occupy the unit place
Case 1: Repetition is allowed (Permutation and Combination Class 11)
If 0 is at the unit place⇒ 4×5×5×1=100
If 5 is at the unit place⇒ 4×5×5×1=100
Total numbers= 100+100=200
Case 2: Repetition is not allowed (Permutation and Combination Class 11)
If 0 is at the unit place⇒ 4×3×2×1=24
If 5 is at the unit place⇒ 3×3×2×1=18
Total numbers= 24+18=42
Que 10: How many 5-digit numbers contain exactly two 4’s in them? (Permutation and Combination Class 11)
Solution: _×_×_×_×_
Case 1: When the ten thousandth digit is 4
Now, we only have four places left. Select a location for the second 4. Now there are 9 digits left to settle in the other three places.
Number of Possible arrangements= 4C1×9×9×9 ……….(i)
Case 2: When 4 is in place other than the ten-thousandth place
Now, 0 cannot be placed in the ten-thousandth place, so we have only 8 options for that place (except 0 and 4). After that, choose two positions for the two 4’s, then arrange the other 9 numbers in the remaining two positions.
Number of Possible arrangements= 8×4C2×9×9 ……….(ii)
Number of possible arrangements= 4C1×93+8×4C2×92
=4×93+8×6×92
=92×(36+48)
=6804
Distribution problems
Que 1: In how many ways can 5 prizes be distributed to 8 students if each student can get any number of prizes?
Solution: Here repetition is allowed because it is mentioned that ‘each student can get any number of prizes.’ (Permutation and Combination class 11)
Here we have 5 prizes and each prize can be given to any of the 8 students or For each prize there are 8 contestants.
So, the number of possible arrangements= 8×8×8×8×8= 85
Que 2: How many ways can a person send an invitation card to 6 of his friends if he has four servants to distribute the card?
Solution: A similar problem is given above. Here each card can be distributed by any of the servants. (Permutation and Combination class 11)
So, the number of possible ways of distribution= 4×4×4×4×4×4= 46
Word formation Problems
Que 1: How many ways can the letters of the word ‘DELHI’ be arranged?
Solution: All alphabets are different. (Permutation and Combination class 11)
There are 5 vacant positions: _ _ _ _ _
The number of possible arrangements= 5×4×3×2×1= 5!= 120
Que 2: How many ways the letters of the word ALLAHABAD be arranged and rearranged?
Solution: Total alphabets= 9 (4 A’s and 2 L’s are present)
The number of possible arrangements= \frac{9!}{4!\times 2!} = 7560
The number of possible rearrangements= 7560 -1=7559 (The word ALLAHABAD is excluded)
Que 3: How many ways do the letters of the word ‘PRACTICAL’ be arranged so that all vowels come together?
Solution: Make a group of all vowels (AIA) and consider it as a single letter ‘X’. (Permutation and Combination class 11)
Now, PRACTICAL= XPRCTCL
The number of possible arrangements of XPRCTCL= \frac{7!}{2!} =2520 (Two C’s)
The number of possible arrangements of X or AIA= \frac{3!}{2!} =3 (Two A’s)
Final result= 2520×3= 7560
Que 4: How many ways do the letters of the word ‘PRACTICAL’ be arranged so that all vowels come at odd places only?
Solution: 1 2 3 4 5 6 7 8 9 (Permutation and Combination class 11)
Step 1: Total odd places= 5
The number of ways to select 3 out of these 5 odd places= 5C3 = \frac{5!}{3!\times (5-3)!} =10
The number of ways 3 vowels (AAI) can be arranged= \frac{3!}{2!} =3
So, the number of possible arrangements of vowels at odd places= 10×3= 30
Step 2: Number of ways 6 consonants are arranged= \frac{6!}{2!} =360
Final result= 30×360= 10,800
Que 5: How many such words can be formed from all the letters of the word PRACTICAL which start with a vowel and end with a consonant?
Solution: 1 2 3 4 5 6 7 8 9 (Permutation and Combination class 11)
Number of choices for the first position= 2 (Vowels: A or I)
Number of choices for the Ninth position= 5 (Consonants: C,L,P,R,T )
Choices for 2nd position= 9-2= 7
Choices for 3rd position= 7-1= 6
Choices for 4th position= 6-1= 5
Choices for 5th position= 5-1= 4
Choices for 6th position= 4-1= 3
Choices for 7th position= 3-1= 2
Choices for 8th position= 2-1= 1
Final result=2×7×6×5×4×3×2×1×5 = 50,400
Que 6: If 8 consonants and 5 vowels are given and we have to form 5 letter words using 3 of the consonants and 2 vowels then how many such words can be formed?
Solution: The number of ways 3 consonants are selected from 8 Consonants= 8C3
The number of ways 2 vowels are selected from 5 vowels= 5C2
Now, the number of possible arrangements of these 5 letters= 5!
Final result= 8C3×5C2×5! (Permutation and Combination class 11)
=\frac{8!}{3!\times 5!}\times \frac{5!}{2!\times 3!}\times 5!.
=67,200
Concepts of Probability: Click Here
The Dictionary Problem
Que 1: The word ‘ALLAHABAD’ is rearranged in alphabetical order in a special dictionary. Find the position of the word ‘LABADALAH’ in the dictionary?
Solution: The first word in the dictionary is ‘AAAABDHLL’ (Permutation and Combination class 11)
Step 1: Lock the position of the first letter (A): AAAABDHLL
The number of ways, rest 8 letters can be arranged= \frac{8!}{3!\times 2!} (3 A’s and 2 L’s)
Step 2: Lock the position of the first letter (B): BAAAADHLL
The number of ways, rest 8 letters can be arranged= \frac{8!}{4!\times 2!} (4 A’s and 2 L’s)
Step 3: Lock the position of the first letter (D): DAAAABHLL
The number of ways, rest 8 letters can be arranged= \frac{8!}{4!\times 2!} (4 A’s and 2 L’s)
Step 4: Lock the position of the first letter (H): HAAAABDLL
The number of ways, rest 8 letters can be arranged= \frac{8!}{4!\times 2!} (4 A’s and 2 L’s)
Step 5: Lock the position of the first three letters (LAA): LAAAABDHL
The number of ways, the rest 6 letters can be arranged= \frac{6!}{2!} (2 A’s)
Step 6: Lock the position of the first five letters (LABAA): LABAAADHL
The number of ways, rest 4 letters can be arranged= 4!
Step 7: LABADAAHL
LABADAALH
LABADAHAL
LABADAHLA
LABADALAH (Permutation and Combination class 11)
Number of arrangements =5
Final result= \frac{8!}{3!\times 2!}+3\times \frac{8!}{4!\times 2!}+\frac{6!}{2!}+4!+5.
=3360+ 2520+ 360+ 24+5
=6269
Counting of Shapes
There are 32 points on a plane of which 9 are collinear. Now solve the following problems:
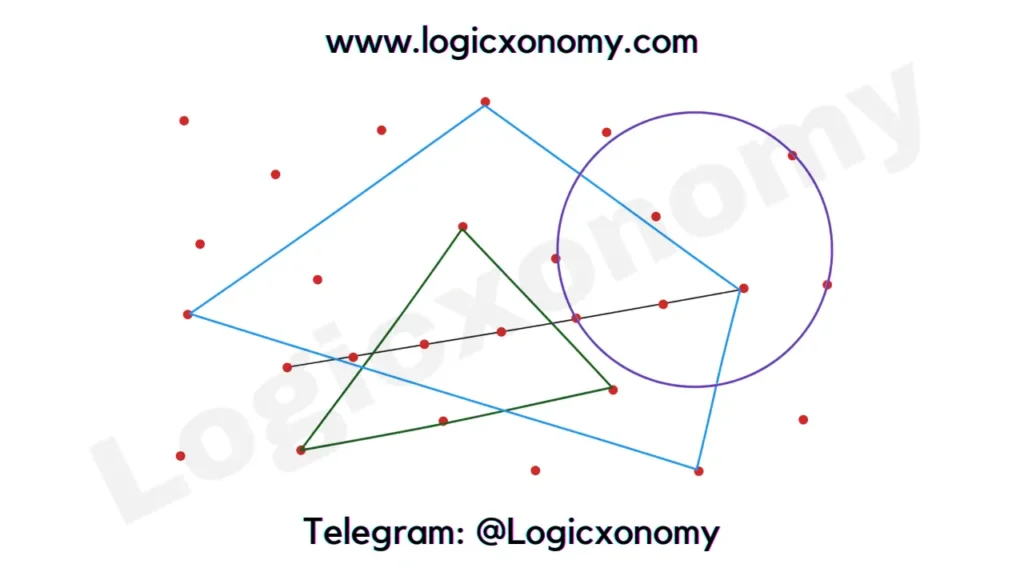
(a) How many straight lines can be drawn? (Permutation and Combination class 11)
Two points are needed to draw a line. So, the number of possible straight lines that can be drawn with 32 non-collinear points= 32C2
Number of possible straight lines that can be drawn with 9 non-collinear points= 9C2
Here, 9 points are collinear so only one line can be drawn through it instead of 9C2
The required number of lines= 32C2 – 9C2 +1 =461
(b) How many triangles can be formed? (Permutation and Combination class 11)
The number of triangles formed with 32 Non-Collinear points= 32C3
The number of triangles formed with 9 Non-Collinear points= 9C3
The required number of Triangles= 32C3 – 9C3 =4876
(c) How many Quadrilaterals can be formed? (Permutation and Combination class 11)
The number of Quadrilaterals formed with 32 Non-Collinear points= 32C4
The number of Quadrilaterals formed by choosing three points from 9 collinear and one from the rest 23 non-collinear points= 9C3×23C1
The number of Quadrilaterals formed with 9 non-collinear points= 9C4
The required number of Quadrilaterals= 32C4 – 9C3×23C1 – 9C4
(d) How many Circles can be drawn? (Permutation and Combination class 11)
There is a Circumcircle of each triangle. So, make it simple and find the number of triangles instead of Circles.
The required number of Circles= 32C3 – 9C3 =4876
Que: How many triangles can be formed by joining red points, which are placed on the sides of the triangle? (Permutation and Combination class 11)
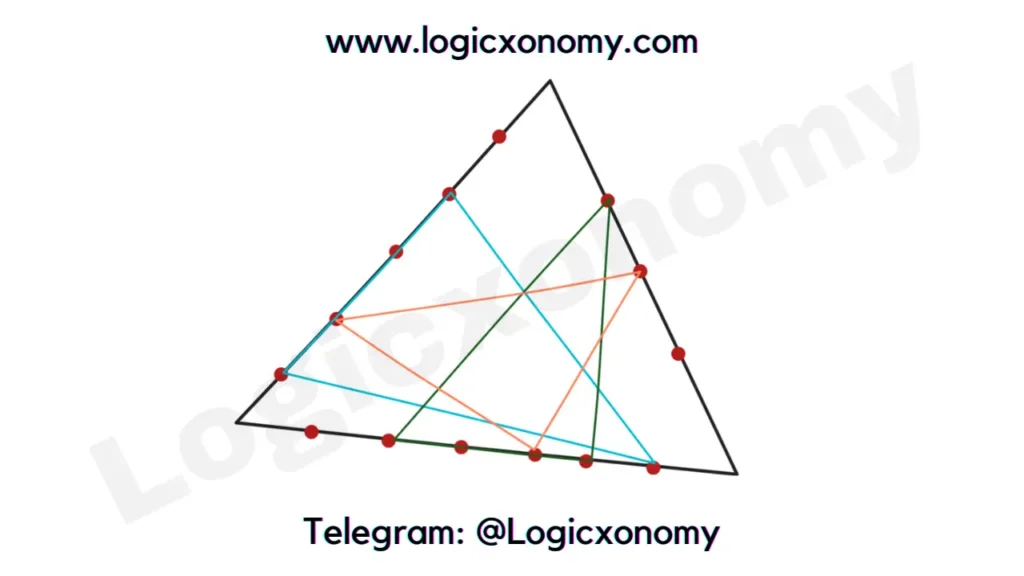
Solution: Total number of red points= 5+6+3= 14
The number of triangles formed with 14 non-collinear points= 14C3
The number of triangles formed with 5 non-collinear points= 5C3
The number of triangles formed with 6 non-collinear points= 6C3
The number of triangles formed with 3 non-collinear points= 3C3
The required number of Triangles= 14C3 – 5C3 – 6C3 – 3C3
Fast Calculation tricks (Mental Maths): Click Here
Que: If a Polygon has 54 diagonals then find the number of its sides? (Permutation and Combination class 11)

Solution: Let, the Polygon has ‘n’ vertices.
The total number of straight lines that can be drawn with these ‘n’ points= nC2
The number of diagonals= Number of all straight lines – Number of the sides of the Polygon
The number of diagonals= nC2 – n
=\frac{n!}{2!\times (n-2)!} -n.
=\frac{n\times (n-1)\times (n-2)!}{2\times (n-2)!}-n.
=\frac{n^{2}-n}{2}-n.
=\frac{n\times (n-3)}{2}.
Given, \frac{n\times (n-3)}{2}=54.
n\times (n-3)=108.
n=12
So, it’s a Dodecagon.
Que: How many rectangles can be formed in a Chessboard?

Solution: There are 9 horizontal and 9 vertical lines present on a Chessboard. Now, to form a rectangle we have to choose any two horizontal and two vertical lines. (Permutation and Combination class 11)
So, the required number of rectangles= 9C2×9C2 =1296
Circular Seating Arrangement
Let if there are ‘n’ members invited to a party. Now we have to find the number of ways they can sit around a round table. (Permutation and Combination class 11)

Fix the place of any one person and calculate the possible arrangement of other n-1 people.
Now, the number of possible arrangements= (n-1)!
In how many ways can the ‘n’ beads be arranged to make a bracelet or necklace?
Here clockwise and anti-clockwise arrangements are identical. So possible number of arrangements= \frac{(n-1)!}{2}
Que 1: There are ‘n’ men sitting around a circular table on distinct chairs. Every possible pair except the one sitting adjacent to each other sings a 2-minutes song one after the other. Find the value of ‘n’ if the total time taken is 88 minutes?

Solution: The first member of the pair can be selected by ‘n’ ways and another by ‘n-3’ ways because the first one and its adjacent two men have to be removed from counting the next possibility. (Permutation and Combination class 11)
Total Possible arrangements= \frac{n\times (n-3)}{2}
Note: The pair of A-B and B-A is identical. So, We have to divide n×(n-3) by 2 to eliminate the redundancy.
Total time taken to complete the song= \frac{n\times (n-3)}{2}\times 2 minutes
n×(n-3)=88 (Given)
n=11
Que 2: 28 people have been invited to the party. In how many ways can the guests and the host be seated around the table so that two particular people are always on either side of the host?

Solution: First, make a group of three people (the host and two particular guests, who are sitting on either side of him) and count them as a single entity. (Permutation and Combination class 11)
So, the new count of people, sitting around the circular table= 26+1=27
The number of ways to arrange these 26 people= (27-1)!= 26!
Two guests in a group of 3 can also be arranged in 2! Ways
So, the required number of arrangements= 26!×2!
Que 3: There are 20 people among whom two are sisters. Find the number of ways in which we can arrange them around a circular table so that there is exactly one person between two sisters?
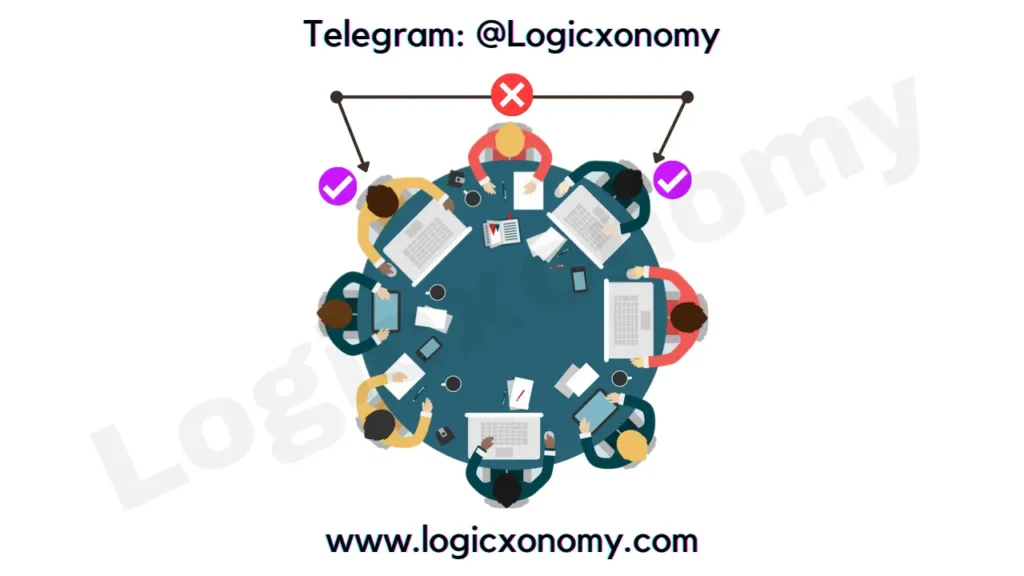
Solution: First, fix the positions of the two sisters (which can be arranged among themselves in 2! ways).
Now, the number of ways to arrange the rest 18 people= 18!
The required number of arrangements= 18!×2!
Que 4: In how many ways 7 boys and 7 girls can sit around a round table so that no two boys or girls can sit next to each other?
Solution: First, arrange 7 boys around a circle. The number of possible arrangements= (7-1)!= 6!
Now 7 girls can be arranged at 7 places in 7! ways.
The required number of arrangements= 6!×7!
Linear Seating arrangement
Que 1: There are 9 orators A, B, C, D, E, F, G, H, and I. In how many ways can the arrangement be made so that A always comes before B and B before C? (Permutation and Combination class 11)
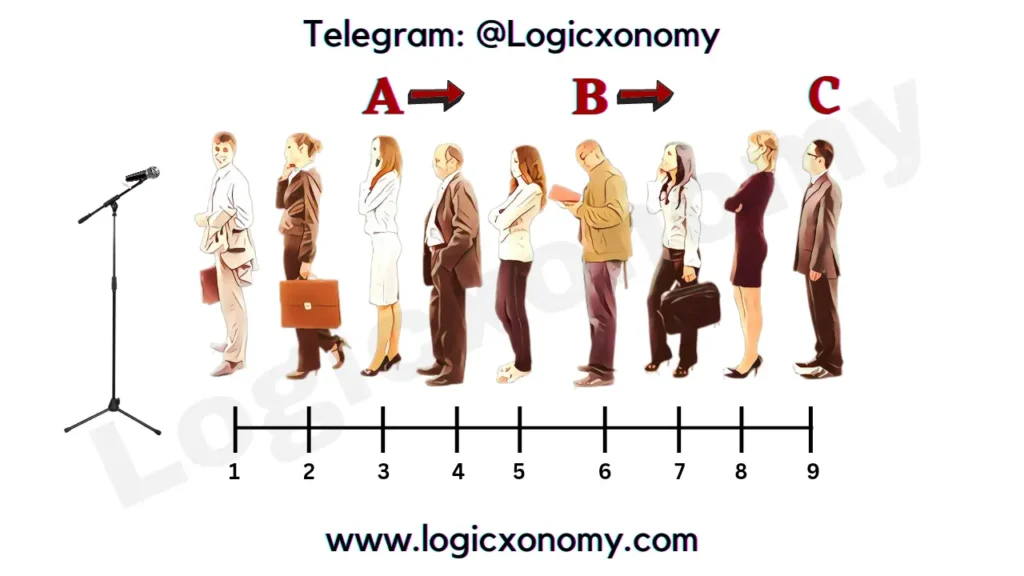
Solution: Number of ways to select three such positions in which order of A then B and then C is maintained= 9C3 =\frac{9!}{3!\times 6!}
Note: The Order of A-B-C can’t be altered so here we are using the Combination.
The number of ways to arrange the rest 6 members= 6!
The required number of arrangements= \frac{9!}{3!\times 6!}\times 6!=\frac{9!}{3!}
Que 2: In a linear seating arrangement, how many ways 5 MBA and 6 LAW students can be arranged together so that no two MBA’s are side by side? (Permutation and Combination class 11)

Solution: 6 Law students can be organized in 6! Ways.
Now, we have 7 positions, which can fulfill the required conditions. We can select 5 positions out of these 7, in 7C5 ways.
The required number of arrangements= 7C5×5!×6!
= \frac{7!}{5!\times 2!}\times 5!\times 6!
= 21×5!×6!
= 1814400
Que 3: Five boys and three girls are sitting in a row. In how many ways can they be seated so that not all girls sit side by side? (Permutation and Combination class 11)
Step 1: If all girls are sitting together then this group of three acts as a single entity (in which all three can be arranged in 3! ways internally).
The new count of members= 5 boys + 1 group of girls= 6
It can be arranged in 6! Ways.
The required number of arrangements, when all girls sitting together= 3!×6!
Step 2: The total possible arrangements= 8!
Now, the required result= 8! – 3!×6!= 36,000
Distribution of identical items
Case 1: In how many ways ‘n’ identical things are distributed among ‘r’ distinct groups so that each may get any number of things including zero.
^{n+r-1}C_{r-1}.
Ex: In how many ways, 32 identical balls are distributed among 5 people such that each of them can get any number (including Zero) of balls. (Permutation and Combination class 11)
The number of such ways= ^{32+5-1}C_{5-1}= ^{36}C_{4}
Case 2: In the above case if each group gets at-least one thing or the case of a non-empty group.
The number of ways= ^{n-1}C_{r-1}
Concept of Case 1:
Let ‘n’ identical things are distributed among ‘r’ distinct groups, separated by r-1 separators (‘|’)
x_1+x_2+x_3+x_4+…….+x_r= n.
x_1 | x_2 | x_3 | x_4 |……..| x_r.
Total elements= n things + (r-1) separators= n+r-1
The number of ways to arrange these n+r-1 elements= (n+r-1)!
Here ‘n’ things are identical. So to eliminate redundancy in counting we have to divide the result by n!
Similarly, r-1 separators are also identical so the result has to be divided by (r-1)!
Final result= \frac{(n+r-1)!}{n!\times (r-1)!} = ^{n+r-1}C_{r-1}
Concept of Case 2: (Permutation and Combination class 11)
In case of non-empty group, replace x_i by y_i+1.
(y_1+1)+(y_2+1)+(y_3+1)+(y_4+1)+…….+(y_r+1)= n.
y_1+y_2+y_3+y_4+………+y_r= n-r.
It Means, in the final result of case:1 we have to replace n by n-r.
New result= ^{n-1}C_{r-1}
The selection of zero or more things
The number of ways to select zero or more things out of ‘n’ different things is 2^{n}.
^{n}C_{0}+^{n}C_1+^{n}C_2+^{n}C_3+……….+^{n}C_n=2^{n}.
In the case of n identical things, the final result will be n+1
Concept: In case of identical things we can select 0,1,2,3……, or n things at a time so the result= n+1
Que: In how many ways a bouquet can be formed from 18 different flowers so that it should contain not less than three flowers? (Permutation and Combination class 11)
Solution: ^{18}C_3+^{18}C_4+^{18}C_5+……..+^{18}C_{18}.
=(^{18}C_0+^{18}C_1+^{18}C_2+^{18}C_3+…….+^{18}C_{18})-(^{18}C_0+^{18}C_1+^{18}C_2).
={2^{18}-(1+18+153)}
=262,144 – 172
=261,972
The Classification of Numbers: Click Here
More Permutation and Combination class 11 concepts are coming soon…

