The Cyclic Quadrilateral properties, its Theorems, and Formulas with proof. In this chapter, we will learn some very important geometry hacks which can help us in quick solutions to complex problems in the examination.
Introduction
Circle: A closed two-dimensional curved shape whose all boundary points are equidistant from its center.
Secant: A straight line that intersects the circle at two distinct points.
Chord: The straight line whose endpoints lie on the circumference of the circle. If a Chord passes through the center of the circle, it is called the ‘Diameter’ of the circle.
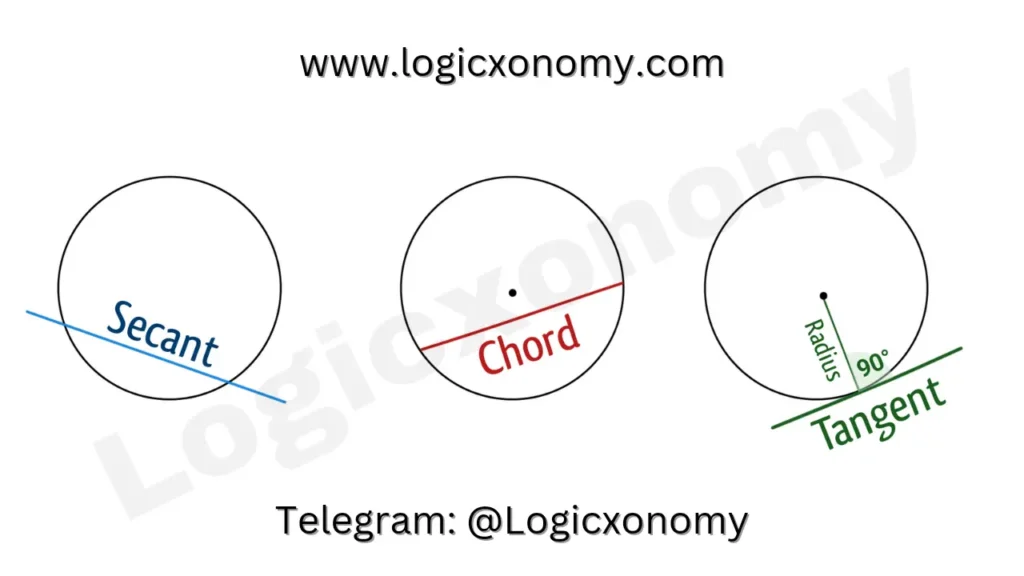
Radius: A straight line, meeting the center of the circle to its circumference.
Tangent: A straight line outside the circle, that touches it on a single point. Tangent is always perpendicular to the radius of the circle.
There are an infinite number of Tangents can be drawn around the circle because on each point on its circumference, a tangent can be drawn.
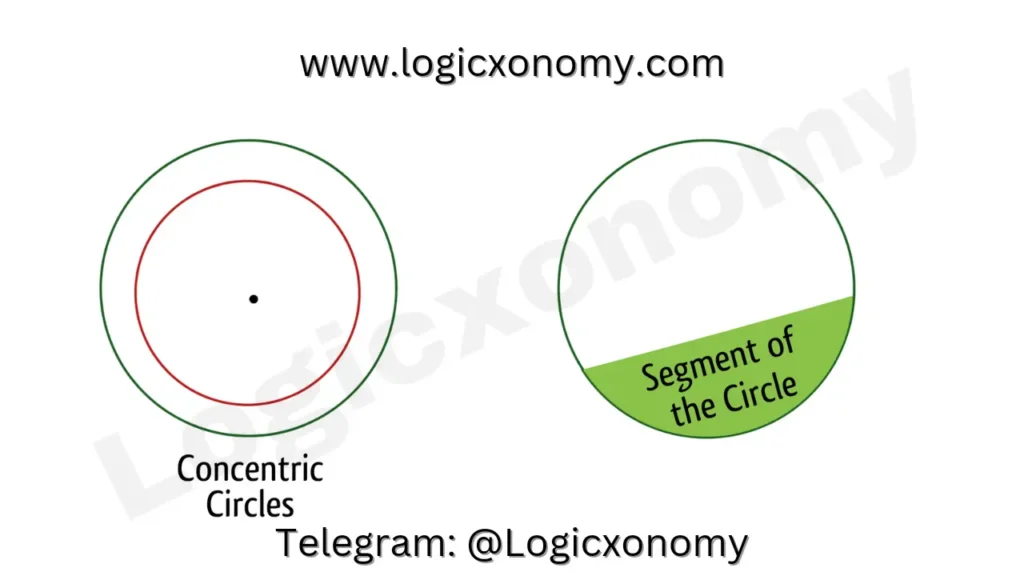
Concentric Circles: The Circles that share the same center are called concentric circles.
The segment of the Circle: A chord divides a circle into two parts these are called its segments.
A region in the circle, bounded by a chord and an arc (part of the circumference) is called the segment of the Circle.
Properties of the Chord
- Angles subtended on the boundary of the circle (in the same segment), by a chord are always equal.
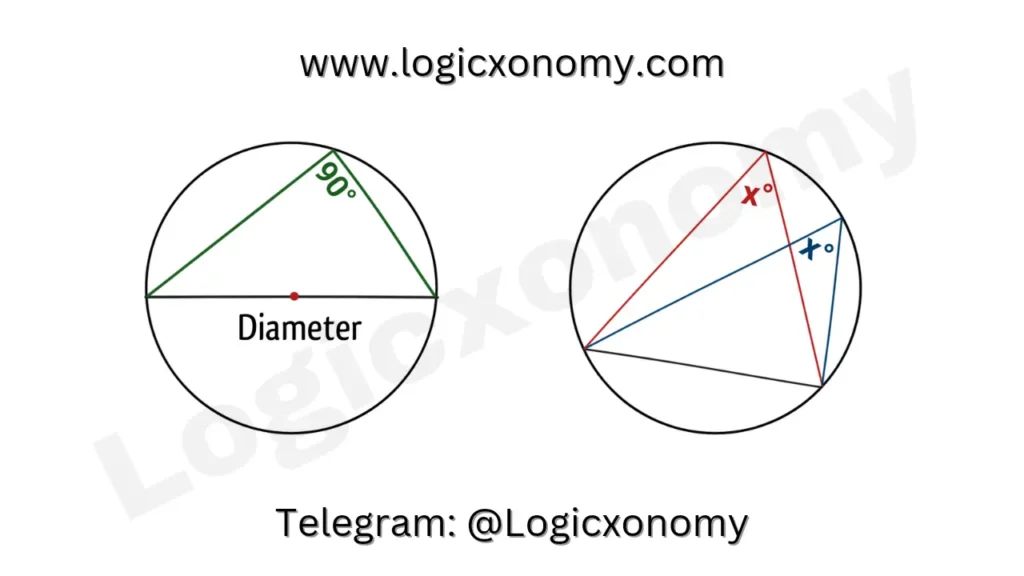
- The largest chord (Diameter) always subtends 90° angle on the boundary of the circle.
- The perpendicular bisector of the chord always passes through the center of the circle. A straight line meeting the center of the circle to the midpoint of the chord bisects the chord perpendicularly.
- The angle formed between the chord and the tangent is always equal to the angle that the chord subtends at the boundary of the circle in its opposite segment.
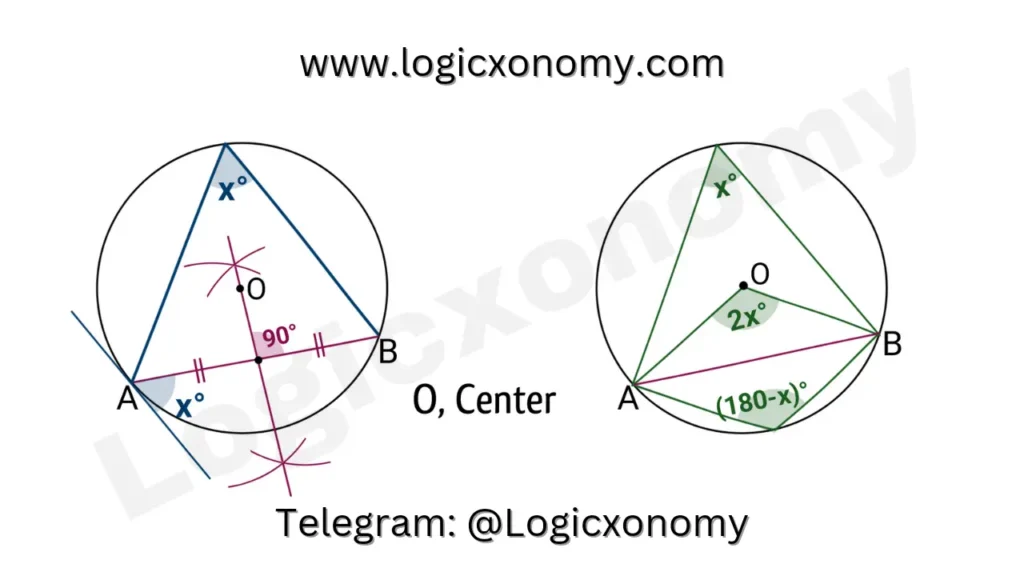
- Two angles, subtended by the Chord on the boundary of the circle in its opposite segments are supplementary angles means the sum of such angles is always 180°. (Cyclic Quadrilateral Properties)
- In the same segment of the circle, the angle subtended by a Chord on its Center is double the value of the angle subtended by the same chord on the boundary of the circle.
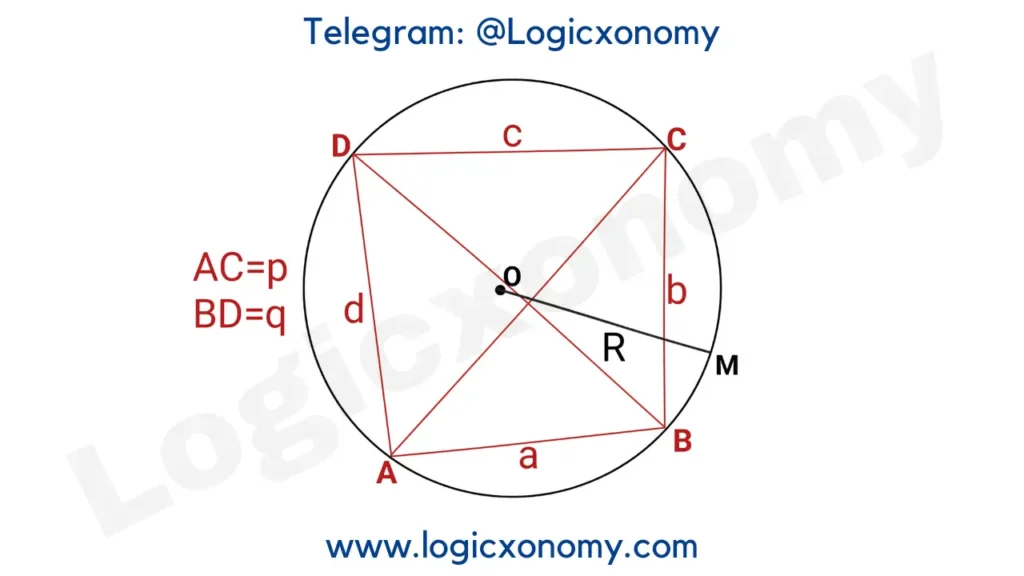
Cyclic Quadrilateral Properties
All vertices of a Cyclic Quadrilateral lie on the circumference of the circle. So, all its sides are the chords of the circle.
The perpendicular bisectors of the sides of a Cyclic Quadrilateral are always Concurrent, and the intersection point of perpendicular bisectors is the Center of its Circumcircle.
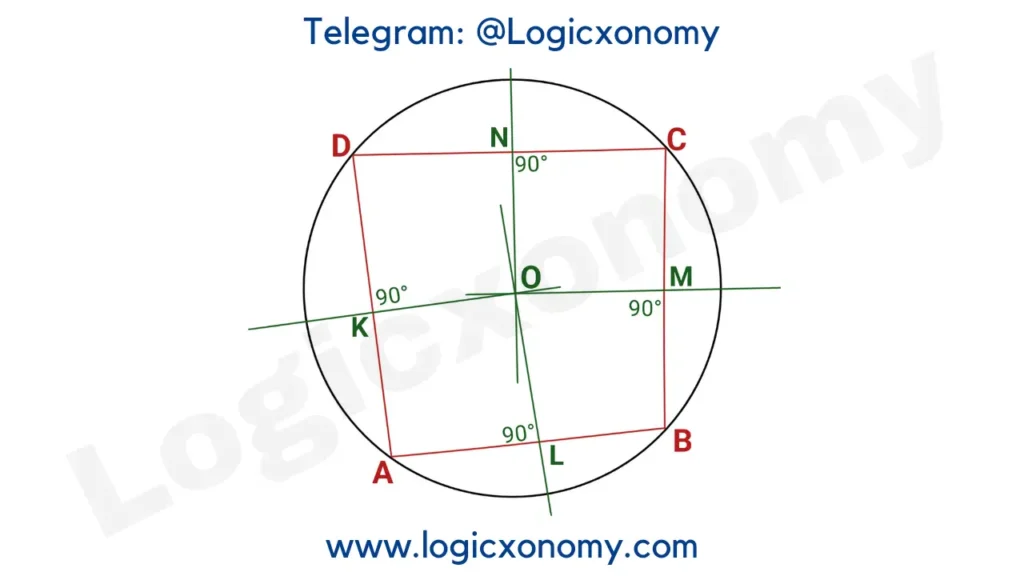
In this figure L, M, N, and K are the midpoints of the respective sides. O is the center of the Circumcircle. (Cyclic Quadrilateral Properties)
OA=OB=OC=OD=R
Where R is the radius (The Circumradius) of the Circumcircle.
- The sum of the opposite angles is 180° (∠A+∠C=180°, ∠B+∠D=180°).
- The exterior angle at any vertex is the same as the internal angle opposite to that vertex.
- For given side lengths of a Quadrilateral, the area of a Cyclic Quadrilateral is maximum.
Geometry Basics and Formulas: Click Here
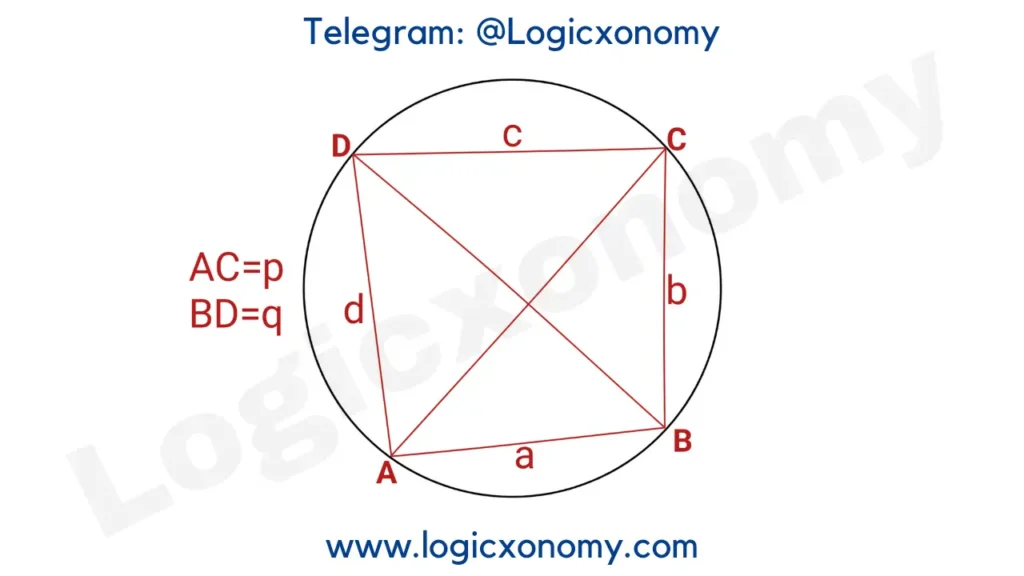
Ptolemy’s Theorem
For a given Cyclic Quadrilateral, According to Ptolemy’s Theorem “The product of the lengths of diagonals is equal to the sum of the products of opposite sides.” (Cyclic Quadrilateral Properties)
p×q=a×c + b×d
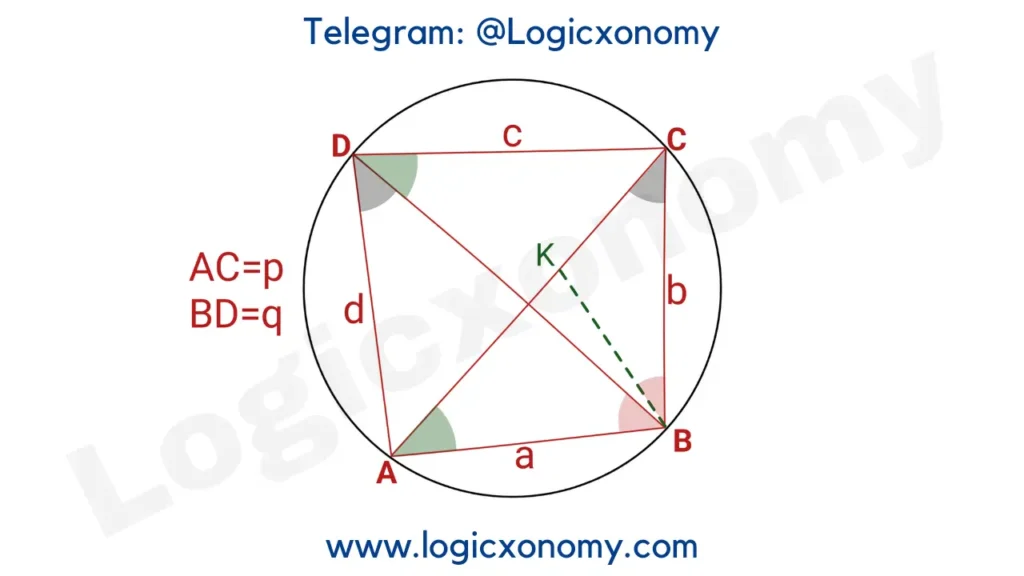
Step 1: Draw a line BK such that ∠CBK = ∠DBA
∠ADB = ∠ACB (Angles subtended by the same chord, AB)
∠BAC = ∠BDC (Angles subtended by the same chord, BC)
Similarity (1): △BCK \sim △BDA (Similar Triangles)
\frac{CK}{DA}=\frac{BC}{BD}.
\frac{CK}{d}=\frac{b}{q}.
CK=\frac{bd}{q} ………..(i)
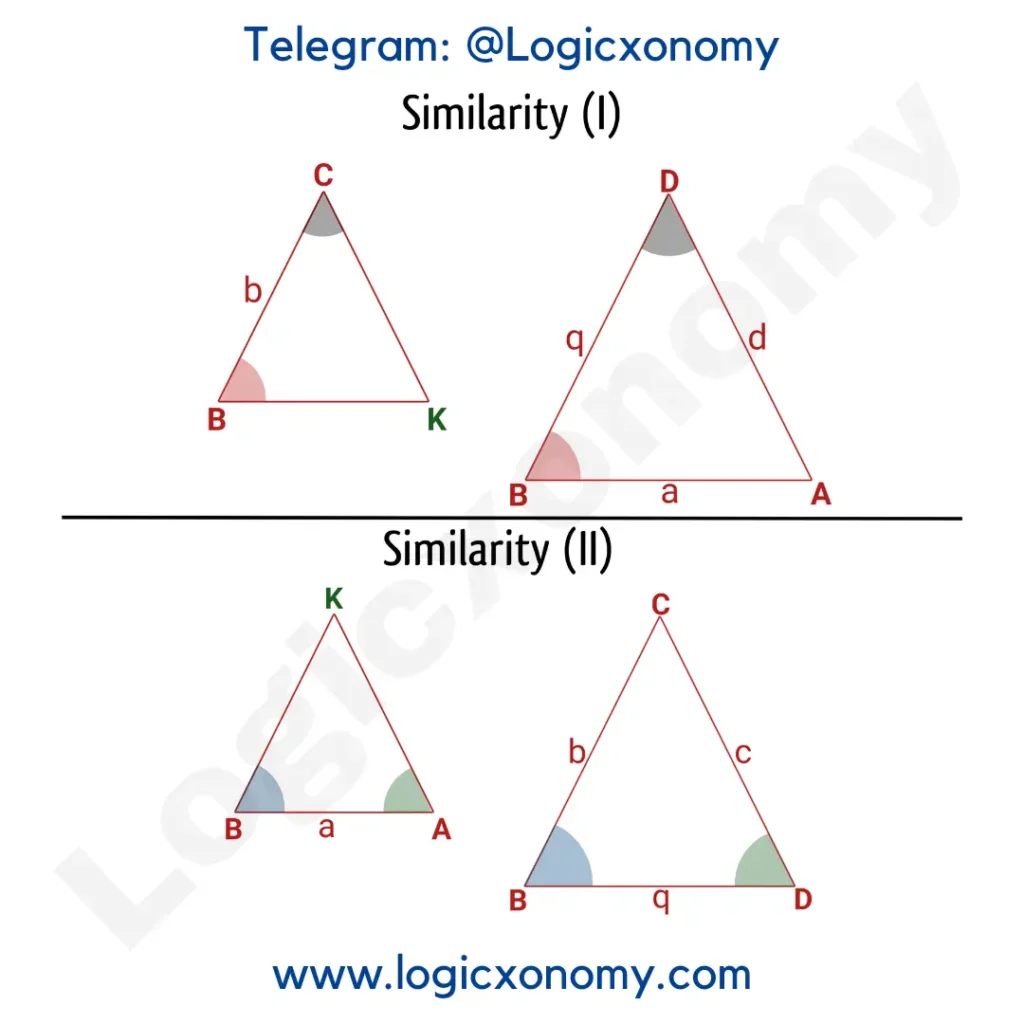
Similarity (2): △BKA \sim △BCD
\frac{AK}{CD}=\frac{AB}{BD}.
\frac{AK}{c}=\frac{a}{q}.
AK=\frac{ac}{q} ………..(ii)
Add both equations:
CK+AK=\frac{bd}{q}+\frac{ac}{q}.
AC=\frac{1}{q}(bd+ac).
p=\frac{1}{q}(bd+ac).
pq=(ac+bd)
Ptolemy’s Inequality
For the given Quadrilateral ABCD, AB×CD + BC×AD ≥ AC×BD
Where equality holds if and only if the Quadrilateral is Cyclic. (Cyclic Quadrilateral Properties)
The ratio of the Diagonals
Let the length of the Circum-radius of the quadrilateral ABCD be R. It is also the circum-radius of △BAD and △BCD. (Cyclic Quadrilateral Properties)
For △BAD,
R=\frac{AB\times AD\times DB}{4\times ar(\triangle BAD)}.
ar(\triangle BAD)=\frac{adq}{4R} ………….(i)
For △BCD,
R=\frac{DC\times CB\times DB}{4\times ar(\triangle DCB)}.
ar(\triangle DCB)=\frac{cbq}{4R} ………….(ii)
Add both equations:
ar(\triangle BAD)+ar(\triangle BCD)=\frac{adq}{4R}+\frac{cbq}{4R}.
ar(\square ABCD)=\frac{q}{4R}(ad+bc) ……..(iii)
Similarly using △ABC and △ADC,
ar(\square ABCD)=\frac{p}{4R}(ab+dc) ……….(iv)
From equations (iii) and (iv)
\frac{p}{4R}(ab+dc)=\frac{q}{4R}(ad+bc).
\frac{p}{q}=\frac{(ad+bc)}{(ab+cd)}

The length of Diagonals
pq=(ac+bd) ……….(i)
\frac{p}{q}=\frac{(ad+bc)}{(ab+cd)} ……….(ii)
p^{2}=pq\times \frac{p}{q}.
=(ac+bd)\times \frac{(ad+bc)}{(ab+cd)}.
p=\sqrt{\frac{(ac+bd)(ad+bc)}{(ab+cd)}}.
q^{2}=pq\times \frac{q}{p}.
=(ac+bd)\times \frac{(ab+cd)}{(ad+bc)}.
q=\sqrt{\frac{(ac+bd)(ab+cd)}{(ad+bc)}}.
Parameshvara’s Formula
This formula is used to find the length of the circumradius of a Cyclic Quadrilateral of given side lengths. (Cyclic Quadrilateral Properties)
ar(\square ABCD)=\frac{p}{4R}(ab+dc).
p=\sqrt{\frac{(ac+bd)(ad+bc)}{(ab+cd)}}.
After putting the value of p in the formula
k=\frac{1}{4R}\sqrt{(ab+cd)(ac+bd)(ad+bc)}.
Here, k is the area of the Quadrilateral (Use Brahmagupta’s formula to find the area)
k=\sqrt{(s-a)(s-b)(s-c)(s-d)}.

R=\frac{1}{4}\sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}.
The Brahmagupta’s Formula
This formula is used to find the area of the Cyclic Quadrilateral. (Cyclic Quadrilateral Properties)
ar(\triangle BAD)=\frac{1}{2}ad\times Sin(A).
ar(\triangle BCD)=\frac{1}{2}bc\times Sin(C)=\frac{1}{2}bc\times Sin(A).
Note: Sin(C)=Sin(180°-A)=Sin(A) [Cyclic Quadrilateral Properties]
So, ar(\square ABCD)= ar(\triangle BAD) + ar(\triangle BCD).
k=\frac{1}{2}(ad+bc)\times Sin(A).
Here, k represents the area of Cyclic Quadrilateral ABCD.
After squaring both sides:
k^{2}=\frac{1}{4}(ad+bc)^{2}\times (1-Cos^{2}(A)).
k^{2}=\frac{1}{4}(ad+bc)^{2}-\frac{1}{4}(ad+bc)^{2}\times Cos^{2}(A). ………….(i)

In △BAD, (Cosine Formula)
Cos(A)=\frac{a^{2}+d^{2}-q^{2}}{2ad}.
q^{2}=a^{2}+d^{2}-2ad\times Cos(A) ……….(ii)
Similarly in △DCB, (Cosine Formula)
q^{2}=b^{2}+c^{2}-2bc\times Cos(C).
q^{2}=b^{2}+c^{2}+2bc\times Cos(A) ……….(iii)
Note: Cos (C) = Cos(180°-A)= -Cos(A)
From equations (ii) and (iii)
a^{2}+d^{2}-2ad\times Cos(A)=b^{2}+c^{2}+2bc\times Cos(A).
2.Cos(A)(ad+bc)=a^{2}+d^{2}-b^{2}-c^{2}.
\frac{1}{4}(ad+bc)^{2}\times Cos^{2}(A)=\frac{1}{16}(a^{2}+d^{2}-b^{2}-c^{2})^{2} …………..(iv)
Put this value in equation (i)
k^{2}=\frac{1}{4}(ad+bc)^{2}-\frac{1}{16}(a^{2}+d^{2}-b^{2}-c^{2})^{2}.
16\times k^{2}=4\times (ad+bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}.
16\times k^{2}=(2ad+2bc)^{2}-(a^{2}+d^{2}-b^{2}-c^{2})^{2}.
As we know: x^{2}-y^{2}=(x+y)(x-y).
16\times k^{2}=[(b+c)^{2}-(a-d)^{2}]\times [(a+d)^{2}-(b-c)^{2}].
Again apply this formula: x^{2}-y^{2}=(x+y)(x-y).
16\times k^{2}=[(a+b+c-d)(b+c+d-a)]\times [(a+d+b-c)(a+d+c-b)].
Let, the semi-perimeter of \square ABCD= s.
2s=a+b+c+d.
16\times k^{2}=[(2s-2d)(2s-2a)]\times [(2s-2c)(2s-2b)].
16\times k^{2}=16\times (s-a)(s-b)(s-c)(s-d).
k=\sqrt{(s-a)(s-b)(s-c)(s-d)}.
Bretschneider’s formula
This formula calculates the area of a quadrilateral if the length of sides and the sum of opposite angles are given.
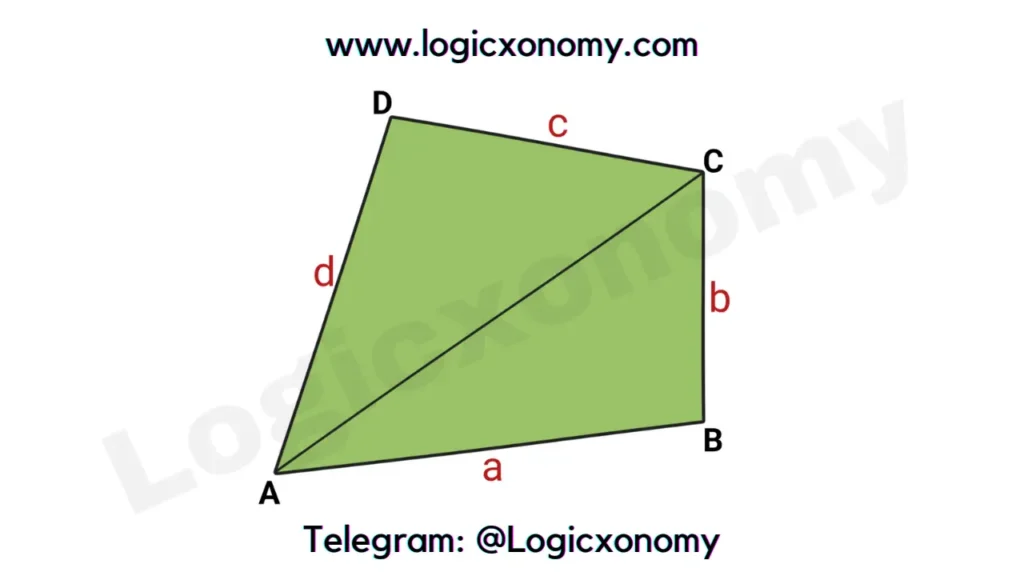
ar(\square ABCD) = ar(△ABC) + ar(△ADC).
k=\frac{1}{2}ab\times Sin(B)+\frac{1}{2}cd\times Sin(D).
4k=2ab\times Sin(B)+2cd\times Sin(D).
Here, k is the area of the Quadrilateral.
After squaring both sides:
16k^{2}=4a^{2}b^{2}\times Sin^{2}(B)+4c^{2}d^{2}\times Sin^{2}(D)+8abcd\times Sin(B)\times Sin(D)………..(i)
In △ABC, Use Cosine Formula
AC^{2}=a^{2}+b^{2}-2ab\times Cos(B) ………..(ii)
AC^{2}=c^{2}+d^{2}-2cd\times Cos(D) ………..(iii)
From equation (ii) & (iii)
a^{2}+b^{2}-2ab\times Cos(B)=c^{2}+d^{2}-2cd\times Cos(D).
2ab\times Cos(B)-2cd\times Cos(D)=a^{2}+b^{2}-c^{2}-d^{2}.
After Squaring both sides:
4a^{2}b^{2}Cos^{2}(B)+4c^{2}d^{2}\times Cos^{2}(D)-8abcd\times Cos(B)\times Cos(D)=(a^{2}+b^{2}-c^{2}-d^{2})^{2} ……(iv)
Add equations (i) and (iv):
Formula: Sin^{2}(\theta)+Cos^{2}(\theta)=1.
16k^{2}+(a^{2}+b^{2}-c^{2}-d^{2})^{2}=4a^{2}b^{2}+4c^{2}d^{2}-8abcd\times Cos(B+D).
Formula: Cos(C+D)=Cos(C).Cos(D) – Sin(C).Sin(D)
=(2ab+2cd)^{2}-8abcd-8abcd\times Cos(B+D).
=(2ab+2cd)^{2}-8abcd\times [1+Cos(B+D)].
Formula: Cos(2\theta)=2Cos^{2}(\theta)-1.
=(2ab+2cd)^{2}-8abcd\times (1+2Cos^{2}(\frac{B+D}{2})-1).
=(2ab+2cd)^{2}-16abcd\times Cos^{2}(\frac{B+D}{2}).
16k^{2}+16abcd\times Cos^{2}(\frac{B+D}{2})=(2ab+2cd)^{2}-(a^{2}+b^{2}-c^{2}-d^{2})^{2}.
Formula: x^{2}-y^{2}=(x+y)(x-y).
=[(a+b)^{2}-(c-d)^{2}]\times [(c+d)^{2}-(a-b)^{2}].
Formula: x^{2}-y^{2}=(x+y)(x-y).
=[(a+b+c-d)(a+b+d-c)]\times [(a+c+d-b)(b+c+d-a)].
Formula: 2s = a+b+c+d, Where ‘s’ is the semiperimeter.
=[(2s-2d)(2s-2c)]\times [(2s-2b)(2s-2a)].
=16\times (s-a)(s-b)(s-c)(s-d).
k^{2}=(s-a)(s-b)(s-c)(s-d)-abcd\times Cos^{2}(\frac{B+D}{2}).
k=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\times Cos^{2}(\frac{B+D}{2})}.
Here, You can put B+D or A+C
Cos(\frac{B+D}{2})=Cos(\frac{360°-(A+C)}{2})=-Cos(\frac{A+C}{2}).
After Squaring both sides:
Cos^{2}(\frac{B+D}{2})=Cos^{2}(\frac{A+C}{2}).
In the case of Cyclic Quadrilateral B+D=180° (Cyclic Quadrilateral Properties)
Cos^{2}(\frac{B+D}{2})=Cos^{2}(90°)=0.
k=\sqrt{(s-a)(s-b)(s-c)(s-d)}.
It’s the Brahmagupta’s Formula. (Cyclic Quadrilateral Properties)
Question: Find the area of ◻ABCD, if AB=7, BC=5 cm, CD=4 cm, and DA=6 cm. ∠A=70°, ∠B=115°, ∠C=50° and ∠D=125°?
Solution: Use Bretschneider’s formula:
k=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\times Cos^{2}(\frac{B+D}{2})}.
s=11
a=7, b=5, c=4, d=6
A+C=120°, Cos(60°)=1/2
k=3\sqrt{70} cm^{2}The Quadrilateral, made of tangents
In the given figure, tangents AP = AS
PB = BQ
CR=CQ
DR=DS
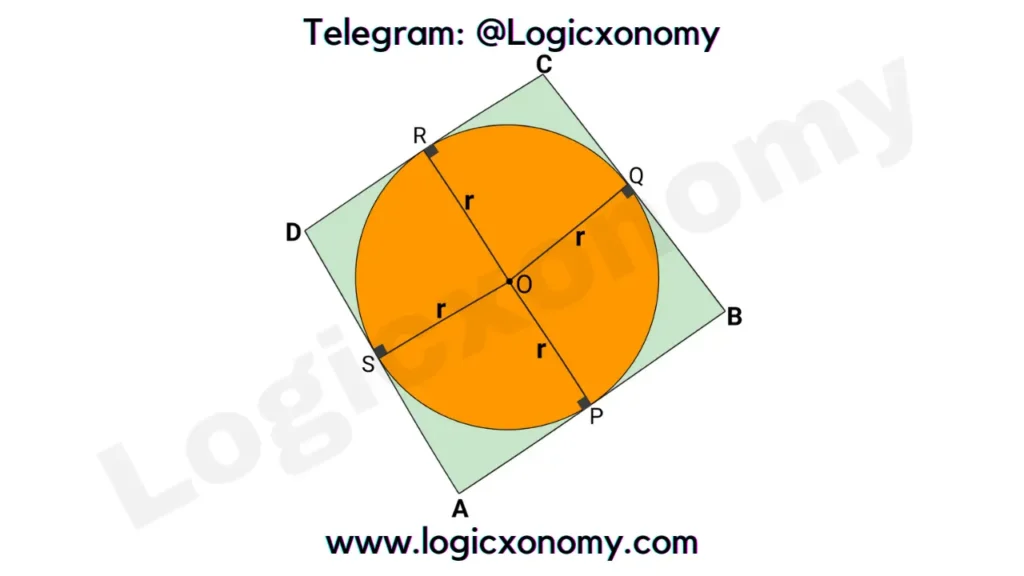
Add all equations:
(AP + PB) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + DC = BC + AD ………(i) [Theorem]
The area of the Quadrilateral, and the inradius
The area of triangle = \frac{1}{2}\times Base\times Height.
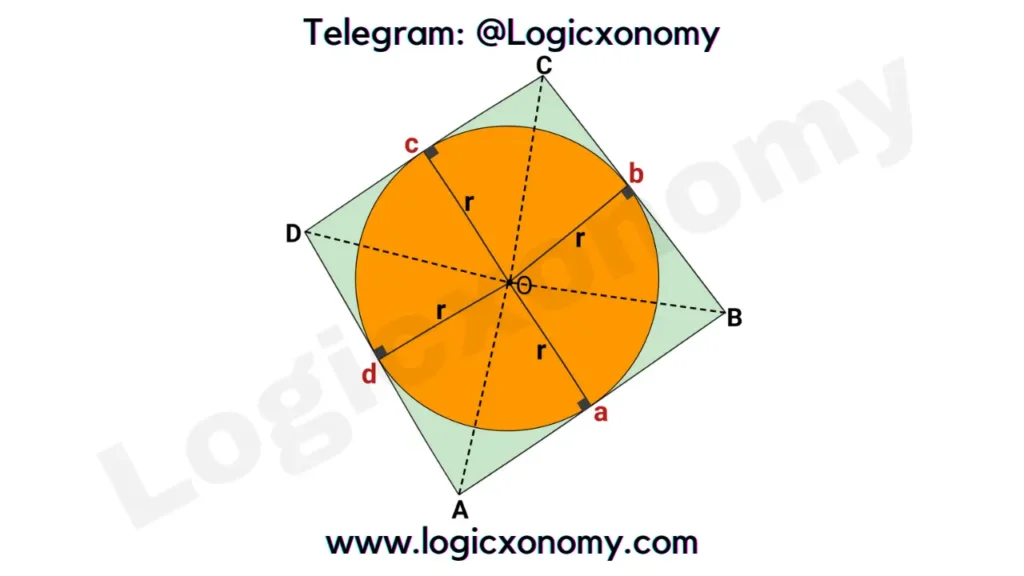
ar(△AOB) = \frac{1}{2}ar.
ar(△BOC) =\frac{1}{2}br.
ar(△COD) = \frac{1}{2}cr.
ar(△DOA) = \frac{1}{2}dr.
ar(\square ABCD) = \frac{1}{2}(ar+br+cr+dr).
Let, ‘k’ is the area of the Quadrilateral and ‘s’ is its semi-perimeter.
k=\frac{a+b+c+d}{2}\times r.
k=s\times r ……….(ii)
Question: In the given figure AB=1 cm, CD=4 cm, and DP : PB = 8 : 3 then find the area of the encircle? (Cyclic Quadrilateral Properties)
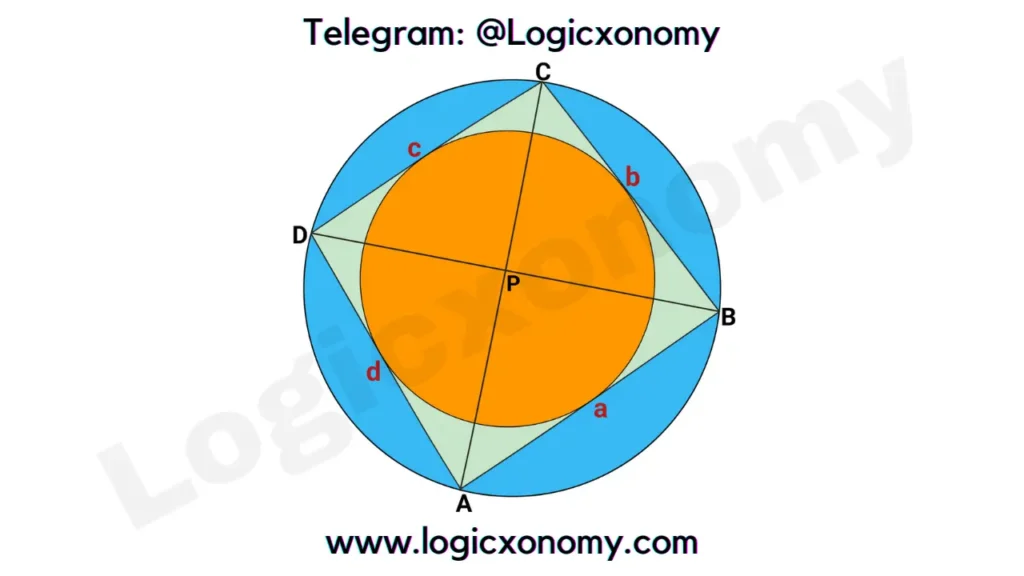
Solution: △DCP \sim △ABP (Similar Triangles)
∠DCA = ∠ABD (Angles subtended by the same chord AD, on the boundary)
∠DPC = ∠APB (Vertically opposite angles)
Given, DP=8x & PB=3x
So, \frac{DP}{AP}=\frac{CP}{PB}=\frac{DC}{AB}.
\frac{8x}{AP}=\frac{CP}{3x}=\frac{4}{1}.
\frac{CP}{3x}=\frac{4}{1}.
CP=12x.
\frac{8x}{AP}=\frac{4}{1}.
AP=2x.
△DAP \sim △CBP.
∠DAC = ∠CBD (Angles subtended by the same chord DC, on the boundary)
∠DPA = ∠CPB (Vertically opposite angles)
So, \frac{DP}{PC}=\frac{AP}{PB}=\frac{AD}{BC}.
\frac{8x}{PC}=\frac{2x}{3x}=\frac{AD}{BC}.
\frac{AD}{BC}=\frac{2}{3}.
Let, AD=2y & BC=3y
Use Theorem: AB + DC = BC + AD
1+4=3y+2y
y=1
So, AD=2 & BC=3
The area of the Cyclic Quadrilateral ABCD, (Use Brahmagupta’s Formula)
k=\sqrt{(s-a)(s-b)(s-c)(s-d)}.
a= 1, b=3, c=4, d=2, and s=5
So, k=\sqrt{24} cm2
To find the area of the incircle use formula: k=s\times r.
5\times r=\sqrt{24}.
r=\frac{\sqrt{24}}{5}.
Area of incircle =\pi r^{2}=\frac{24}{25}\pi cm2
Diagonals of the Cyclic Quadrilateral
Let, O be the intersection point of the diagonals AC & BD. (Cyclic Quadrilateral Properties)

ar(\triangle BAD)=\frac{1}{2}\times ad\times Sin(A).
ar(\triangle BCD)=\frac{1}{2}\times bc\times Sin(C).
Sin(A)= Sin(180°-C)=Sin(C)
\frac{ar(\triangle BAD)}{ar(\triangle BCD)}=\frac{ad}{bc}.
\frac{ar(\triangle ADO)}{ar(\triangle CDO)}=\frac{AO}{OC} ……..(ii)
\frac{ar(\triangle ABO)}{ar(\triangle CBO)}=\frac{AO}{OC} ……..(iii)
Add equations (ii) & (iii)
\frac{ar(\triangle BAD)}{ar(\triangle BCD)}=\frac{AO}{OC} ……..(iv)
Compare equations (i) & (iv)
\frac{AO}{OC}=\frac{a\times d}{b\times c}.
Similarly, \frac{BO}{OD}=\frac{a\times b}{c\times d}.
More Cyclic Quadrilateral Properties are coming soon…

