Probability in maths is a very important and one of the scariest chapters. Permutation and Combination, the set theory, and Probability fall in the same domain. These all chapters are interconnected.
Definition
Probability is the mathematical representation of the possibility (chance) of the occurrence of an event.
Example: (1) Chances of getting head after flipping a coin.
(2) The likelihood of India’s winning the Cricket world cup.
Importance of Probability in Real-Life
(1) Before investing in a business, the estimation of the probability of success is required. (Probability in Maths)
(2) Life insurance companies decide the amount of premium according to life expectancy. Like premium of a person starting insurance at age of 28 is far lower than that person of age 60 because its a very high chance to die soon for the person of age 60.
(3) In the share market, the price fluctuations of a particular share purely depend on the probability of its future success or failure.
Concepts of Permutation and Combination: Click Here
The terminology of Probability
Experiments: An activity, the outcomes of which are not known. The few outcomes of an experiment could be favorable.
Example: One thousand failed Experiments by Thomas Alva Edison during the invention of the Light Bulb. (Probability in Maths)
Random Experiments: If all possible outcomes of an experiment are known but the result of a particular execution is not clear.
Example: In the toss of a coin either Head or Tail would come but which one will come is not clear.
Trial: The numerous attempts, in a particular process.
Example: In the numerous tosses (Trials) of a coin, some results head, and others are tail.
Outcome: The possible result of an event.
Event: A trial, with a clearly defined outcome.
Example: Getting 3 after rolling a Dice.
Equally likely Events: The events with the same possibility of occurrence.
Example: Getting a head or tail after tossing a coin, Getting an even or odd number after randomly picking a natural number.
Sample Space: The set of possible outcomes of all trials.
Example: The Sample Space, after rolling a Dice= {1,2,3,4,5,6}
Impossible Events: The possibility (Probability) of occurrence is Zero.
Example: Getting 7 after rolling a Standard Dice.
Certain Event: Its probability is equal to One because, in each trial, we get only a favorable outcome.
Example: Getting a number that is less than 7 after rolling a Standard Dice.
Elementary Events: An event with only one outcome. The sum of probabilities of all the possible elementary events in an experiment is One. (Probability in Maths)
Example: In a random experiment of tossing a coin there are two elementary events:
(a) Event of getting Head
(b) Event of getting Tail
Getting more than 4 after rolling a Dice is not an elementary event because it has two possible outcomes which are 5 & 6.
Complementary Event: Two events are complementary if the occurrence of one is the surety of not occurring of the other. Such events can’t happen simultaneously.
Example: Getting Head and Tail at the same time after tossing a coin is impossible. (Probability in Maths)
Odds: The ratio of the probability of an event and the probability of its complementary event or the ratio of the number of favorable outcomes and unfavorable outcomes.
The formula of Probability in Maths
Que: What is the probability of getting a number greater than 2 in a throw of normal dice?
Solution: Possible outcomes, n(T)= {1,2,3,4,5,6} ⇨6 events
Required outcomes, n(R)={3,4,5,6} ⇨4 events
Probability= \frac{n(R)}{n(T)} = \frac{2}{3}

The use of Conjunctions (AND & OR)
Que 1: The probabilities of hitting a target by A and B are 1/3 & 1/2 respectively. If one shot is taken by both of them then Find the probability of hitting the target by A & B?
Solution: P(A)=1/3 and P(B)=1/2
The required probability= P(A)×P(B)= \frac{1}{3}\times \frac{1}{2}=\frac{1}{6}
Que 2: In the above problem, find the probability that either A or B hits the target?
Solution: The required probability= P(A)+P(B)= \frac{1}{3}+\frac{1}{2}=\frac{5}{6}.
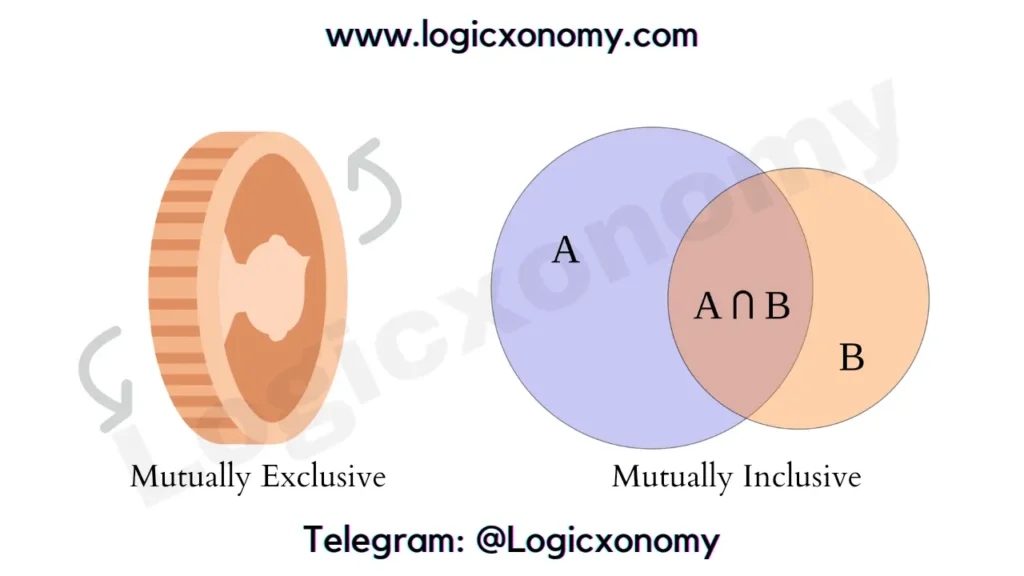
Mutually exclusive events
The two events which can’t occur at the same time are called mutually exclusive events. Example: Getting head and tail at the same time after flipping a coin is impossible. (Probability in Maths)
If the probability of occurrence of an event= P(A)
Then the probability of its exclusive event= P(A’)
Here, P(A’)= 1- P(A)
Example: If two dice are thrown then find the probability [P(A)] of getting a sum more than 3? (Probability in Maths)
Here the minimum possible sum is 1+1=2 and maximum=6+6=12
The Required Sample Space={4,5,6,7,8,9,10,11,12}
First, we would calculate the probability [P(A’)] of getting a sum less than 4.
The total number of outcomes= 6×6=36
The number of require outcomes= {(1,1),(1,2),(2,1)}=3
P(A’)=\frac{3}{36}=\frac{1}{12}.
Now, P(A)= 1-P(A’)= 1-\frac{1}{12}=\frac{11}{12}.
Mutually inclusive events
If two events have some overlap with each other then these are called mutually inclusive events.
Example: If you choose a card from a standard deck then what is the probability of being it a card of Diamond or Queen?
In this case, the first event is ‘choosing a card of Diamond’ and the second event is ‘choosing a card of Queen’. (Probability in Maths)
The probability of getting a card of Diamond, P(A)= \frac{13}{52}.
Note: There are 13 cards of diamond in a deck of 52 cards.
The probability of getting a card of Queen, P(B)= \frac{4}{52}.
Note: There are 4 Queens in a deck of 52 cards.
The probability of getting a Queen of Diamond, P(A⋂B)= \frac{1}{52}.
Note: There is a single Queen of Diamond in a deck of 52 cards.
Then, the required probability, P(A⋃B)= P(A)+ P(B)- P(A⋂B)
P(A⋃B)=\frac{13}{52}+\frac{4}{52}-\frac{1}{52}=\frac{4}{13}.
The Standard Deck of Playing Cards
A standard deck of playing cards consists of 52 cards which are divided into four suits of 13 cards each. These suits are: (Probability in Maths)
1. Heart (Red Color)
2. Club (Black Color)
3. Diamond (Red Color)
4. Spade (Black Color)

Face Cards or Court Cards: The King, Queen, and Jack are the face cards because they depict a person. There are 12 face cards in a deck.
Honour Cards: The Ace, King, Queen, and Jack are called Honour Cards. There are 16 honour cards in a deck.
Number Cards: The cards on which numerals (From 2 to 10) are imprinted. A total of 36 number cards are there in a deck.
Conditional Probability
The probability of occurrence of event A if event B has already occurred, is called Conditional Probability. It is represented by P(A|B).
Example: If you draw a Red card from a standard deck of 52 cards then find the probability that it’s four? (Probability in Maths)
P(Four|Red)=\frac{2}{26}=\frac{1}{13}.
Note: There are 26 Red cards in a deck out of which only 2 are four.
Formula: P(A⋂B)= The joint probability of events A & B.
P(A|B)= Probability of occurring event A if B already occurred.
P(B|A)= Probability of occurring event B if A already occurred.
P(A|B)=\frac{P(A\cap B)}{P(B)}.
In the above question, There are two events:
Event A: Choosing card number 4 from 52 cards
Event B (Already occurred): Choosing the Red card from 52 cards.
P(A⋂B)=\frac{2}{52}.
P(B)= \frac{26}{52}.
P(A|B)= \frac{1}{13}.
Key Points:
(1) \frac{P(A|B)}{P(B|A)}=\frac{P(A)}{P(B)}.
(2) For independent events, P(A|B)=P(A) & P(B|A)=P(B)
(3) For mutually exclusive events, P(A|B) or P(B|A)=0
Que 1: A bag contains 2 blue and 3 red marbles. From which two marbles are drawn one by one without replacement. Find the probability of getting two blue marbles?
Solution: Here we can use Tree Method. (Probability in Maths)

The first marble is drawn:
Case 1: Probability of drawing Blue marble = 2/5
The second marble is drawn:
Case i: Probability of drawing Blue marble = 1/4
Case ii: Probability of drawing Red marble = 3/4
Case 2: Probability of drawing Red marble = 3/5
The second marble is drawn:
Case i: Probability of drawing Blue marble = 2/4
Case ii: Probability of drawing Red marble = 2/4
Here, the Probability of Both marbles to be blue= Probability of the first blue × Probability of the second blue
= \frac{2}{5}\times \frac{1}{4}.
=\frac{1}{10}.
The solution by using the formula: (Probability in Maths)
Event A: First marble is blue
P(A)=2/5
P(B|A)= Probability of second blue marble if the first one is already blue
=1/4
P(A⋂B)=P(A)×P(B|A)
=\frac{2}{5}\times \frac{1}{4}.
=\frac{1}{10}.
Que 2: Two dice are thrown simultaneously and the sum of the numbers obtained is found to be 7. Find the probability that the number 3 appeared at least once?
Solution: The number of total outcomes= 6×6= 36

Event A: The sum of the digits is 7
A= {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)}⇨ 6 outcomes
P(A)=\frac{6}{36}.
Event B: At least one number is 3
B={(3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (1,3), (2,3), (4,3), (5,3), (6,3)}⇨ 11 outcomes
Event A & B both: {(3,4), (4,3)}⇨ 2 outcomes
P(A∩B)=\frac{2}{36}.
P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{1}{3}.
More concepts on Probability in Maths are coming soon…



