The Classification of Numbers is vast and one of the most important topics asked in competitive examinations. It is loaded with many facts, which are important to keep in mind because even a single mistake in language-based math problems, is capable of knocking you out from the competition.
Types of Numbers

In the broader sense, numbers are primarily divided into three parts (Classification of Numbers):
(a) Real Numbers
(b) Imaginary Numbers
(c) Complex Numbers
(a) Real Numbers
Real numbers are the set of positive, negative, decimal, fraction, nth roots of any numbers, etc. That can be marked on an infinitely long number line.
Example: -5, 0, \frac{1}{3}, \sqrt[3]{2}, 1.\overline{26}, 1.543...., 2\frac{3}{5}, etc.
(b) Imaginary Numbers
When a real number is multiplied by an imaginary unit ‘i (iota)’ (where i=\sqrt{-1}), the product is called an Imaginary Number.
Imaginary Numbers are the square root of non-positive real numbers, According to this definition ‘Zero (0)’ is considered the Real and Imaginary Number (0=\sqrt{0}).
Note: Zero (0) is neither a positive nor a negative number. It’s a non-positive as well as a non-negative real number. (Classification of Numbers)
Example: 2i, -5i, \sqrt{3}i ,etc.
(c) Complex Numbers
A combination of real and imaginary numbers, in the form of ‘a+ib’, is called a Complex Number. Where a & b are Real Numbers and iota (i) is an imaginary unit.
Example: 2+3i (Real part=2, Imaginary Part=3i)
Note: All Real numbers are complex numbers with their imaginary part equal to Zero (0). (Classification of Numbers)
| Complex Number | Real Number | Imaginary Number |
| -2+3i | -2 | 3i |
| 5-2i | 5 | -2i |
| -8i | 0 | -8i (Purely Imaginary) |
| 4 | 4 (Purely Real) | 0 |
Types of Real Numbers
Real Numbers can be classified into two major parts (Classification of Numbers):
(a) Rational Numbers
(b) Irrational Numbers
(a) Rational Numbers
Any number that can be expressed in the form of \frac{p}{q}, where p & q are integers (non-decimal, positive, or negative numbers) and q≠0. Rational Numbers include recurring (repeating) and finite decimal numbers.
According to this definition Zero (0) is a rational number because it can be expressed in the form of \frac{p}{q}, where p=0.
Example: \frac{1}{3} , 1, 0, 7,1.2\overline{3} ,1.333..., 2\frac{3}{4}, etc.
Note: \pi=\frac{22}{7} is not actually true, it is just an approximate value of (pi), commonly used in calculations. (Classification of Numbers)
\frac{22}{7}=3.1428571428.....=3.\overline{142857} (Recurring Decimal)
\pi=3.141592653589793238....... (Non-Repeating and Non-Terminating)
Since the value of pi(\pi) is non-terminating and non-repeating, \pi is an irrational number.
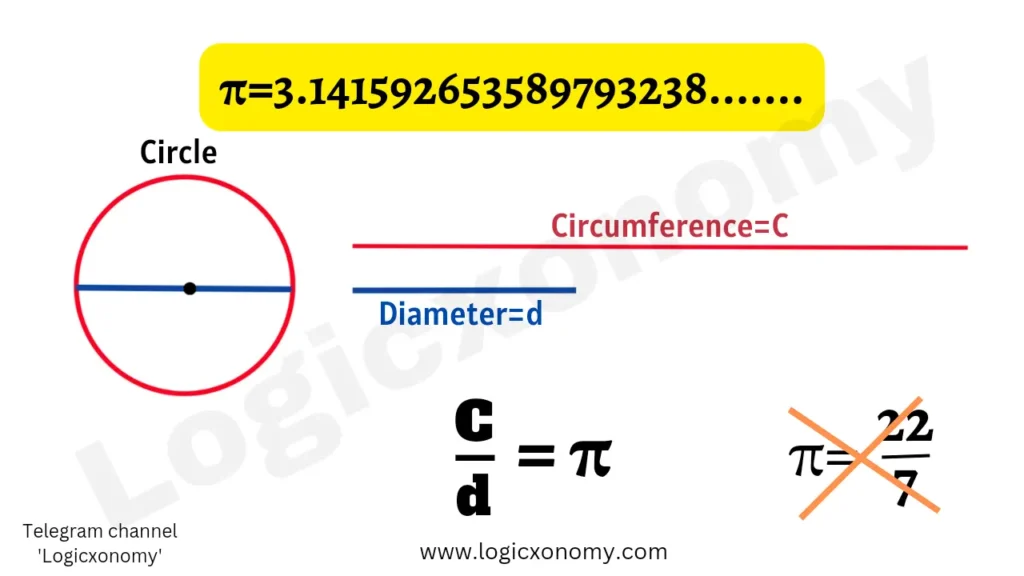
Let, the length of the circumference of a circle be ‘C’ and the length of its diameter be ‘d’ then
\frac{C}{d}=\pi
The earliest use of this Greek letter (\pi) for the ratio of a Circle’s circumference to its diameter is introduced by British Mathematician William Jones in 1706.

(b) Irrational Numbers
Irrational numbers can’t be expressed in the form of \frac{p}{q}, the decimal expansion of an irrational number neither terminates nor repeats.
\sqrt[n]{m} or m^{\frac{1}{n}} , is an irrational number if n and m are positive real numbers but its decimal expansion has an irrational value.
Example: \pi(pi), e , \varphi, \sqrt{2},\sqrt[3]{9}, etc.
\pi=3.14159265.......
e (Euler's Number)=2.71828182......=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+........
\varphi(Golden Ratio)=1.61803398......=\frac{1+\sqrt{5}}{2}.
\sqrt{2}=1.41421356.......

| Numbers | Fractional Form | Rational? |
| 0 | \frac{0}{q} | Yes |
| 1.225 | \frac{49}{40} | Yes |
| -0.1 | -\frac{1}{10} | Yes |
| 0.33333….=0.\overline{3} | \frac{1}{3} | Yes |
| \sqrt{2} | – | No |
| \sqrt{4} | \frac{2}{1} | Yes |
Types of Irrational Numbers
Irrational numbers are divided into two parts (Classification of Numbers):
(a) Surds
(b) Transcendental Numbers
(a) Surds
If the value of \sqrt[n]{x} is an irrational number then it’s a Surd. Here x is a rational number.
Click Here for detailed concepts and tricks of Surds and Indices. (Classification of Numbers)
(b) Transcendental Numbers
A number that is not algebraic, is called a Transcendental Number.
Example: \pi, e, ln(2), 2^{\sqrt{2}}, e^{\pi}, \pi^{e}, i^{i}, etc.
Note: (Classification of Numbers)
- The natural logarithm (base e) of any natural number other than 1, is a Transcendental Number. Example: ln(2)
- If a and b are algebraic numbers (a≠0,1) but b is irrational then a^{b} is a transcendental number. Example: 2^{\sqrt{2}}
Concepts of Algebraic Numbers:
Before starting the concept of Algebraic numbers, we have to know about Polynomials and Polynomial Equations.
Polynomial:
An expression, composed of variables, constants, and exponents which is combined using arithmetic operators like +, -, ÷, and ×, is called a polynomial.
Here the exponents of the variables must be in whole numbers (0,1,2,3….) means fractions and negative exponents are not allowed.
Example:
2x^{2}+3y-7Operators: +,-
Exponents: 2,1 (x^{2}, y^{1})
Coefficient of variables: 2,3
Variables: x,y
Constant: 7
| Expression | Polynomial? |
| 5 | Yes (5x^{0}) |
| 3x | Yes |
| 2y^{2}-\frac{5}{3}x | Yes |
| 3xy^{-1} | No (Negative Exponent) |
| \frac{3}{x+2} | No (Negative Exponent) |
| \frac{x}{2} | Yes |
| \sqrt{2} | Yes |
| \sqrt{x} | No (Fractional Exponent) |
Polynomial Equation: When a polynomial expression equals Zero, called Polynomial Equation.
Example: 3x^{2}+5x-2=0
Algebraic Numbers: It is the solution (root) of a non-zero polynomial equation in one variable, with integer coefficients.
Examples: (i) x^{2}-x-1=0 then x=\frac{1+\sqrt{5}}{2}
(ii) x^{4}+4=0 then x=(1+i)
Here both the values of x are algebraic numbers.
Note: \pi can not be the root of a polynomial that has integer coefficients, so it’s a non-algebraic number.
Types of Rational Numbers
The Rational Numbers are divided into three parts: (Classification of Numbers)
(a) Decimal numbers
(b) Fractions
(c) Integers

(a) Decimal Numbers
A decimal number consists of two parts, a whole and a fractional part separated by a ‘.’ (Decimal Point) sign.
Example: 1.25, 2.3, 0.33, 1.41356……, etc.
Decimals can be further divided into two parts: (Classification of Numbers)
(i) Terminating (Finite) Decimals: This type of decimal number has an end digit after a decimal point or has a finite number of decimal places.
Example: 1.5, 2.4172, etc.
(ii) Non-Terminating Decimals: This type of decimal number doesn’t have an end digit or it goes on indefinitely. Non-Terminating decimal numbers can be further divided into two types: (Classification of Numbers)
- Repeating (Recurring Decimals): The numbers which are uniformly repeated after the decimal point, are called Recurring decimals. It can be represented by drawing an over-line (Bar Sign) on repeating digits.
Example: 1.3333....=1.\overline{3}.
0.25725725...=0.\overline{257}.
3.426565656...=3.42\overline{65}.
2. Non-Repeating Decimals: This type of number is non-terminating and non-repeating in nature. So, it falls in the category of Irrational Numbers.
Example: 1.2357821….., 0.5732182……, etc.
(b) Fractions
If a whole object is divided into ‘n’ equal parts then each part is termed as a Portion. If we select ‘k’ portions out of these then in fractions it is represented as \frac{k}{n}.
k, the number of parts we have
n, the Total number of parts
Example: 3 out of 5 girls can be represented in fractions as \frac{3}{5}.
Fractions can be further classified into three parts: (Classification of Numbers)
(i) Proper Fractions: If the numerator value of a fraction is less than its denominator.
Example: \frac{5}{7}, \frac{1}{2}, \frac{3}{5}, etc.
(ii) Improper Fractions: If the numerator value of a fraction is greater than or equal to its denominator.
Example: \frac{5}{4}, \frac{7}{3}, \frac{11}{11}, etc.
(iii) Mixed fractions: When a fraction consists of two parts, a whole number, and a fractional part then it is called a Mixed Fraction.
Example: 2\frac{5}{7}, 8\frac{1}{2}, etc.
# How to convert an Improper Fraction into a Mixed Fraction (Classification of Numbers)
Que: Convert \frac{13}{5} into a Mixed fraction?
Step 1: Divide 13 by 5.
Quotient=2
Divisor=5
Remainder=3
Step 2: Mixed fraction= Quotient\frac{Remainder}{Divisor}=2\frac{3}{5}.
# How to convert a Mixed Fraction into an improper Fraction (Classification of Numbers)
2\frac{3}{5}=2+\frac{3}{5}=\frac{10+3}{5}=\frac{13}{5}.
(c) Integers
Integer means whole or intact. The positive or Negative numbers including Zero (0), which have no decimal or fractional part are called Integers.
It is expressed as Z={….., -2, -1, 0, 1, 2, …….}
Integers are divided into two parts:
- Whole Numbers: A set of all positive integers and Zero (0) is called Whole Numbers.
W={0,1,2,3,4,5…… }
Whole numbers are further divided into two parts:
(i) Zero(0)
(ii) Natural Numbers: A set of all positive integers is called Natural Number. N={1,2,3,4,…… }
- Negative Numbers: A set of all negative integers is called Negative Numbers (-1,-2,-3,-4,….. ).
Numeral Symbols
R, Real Numbers
Z, Integers
N, Natural Numbers
Q, Rational Numbers
P, Irrational Numbers
C, Complex Numbers
W, Whole Numbers
Discrete and Continuous Numbers
Natural numbers, Whole numbers, Integers, and Rational Numbers are Discrete Numbers. Discrete numbers are finite, numeric, countable, and non-negative Integers.
Real Numbers are continuous Numbers because it is impossible to count real numbers existing between any two real numbers (it’s infinite).
Very Special Numbers
- Even and Odd Numbers
- Prime Numbers
- Co-Prime Numbers
- Composite Numbers
- Perfect Numbers
- Deficient Numbers
- Abundant Numbers
- Happy Numbers
- Narcissistic Numbers
- Palindromic Numbers
- Fermat Number
- Kaprekar Number
- Sierpinski Numbers
- Riesel Numbers
- Sociable Numbers
- Harshad/Niven Numbers
- Mersenne Numbers
- Armstrong Numbers
- Wieferich Prime Numbers ……. and many more
Click the link for details: Types of Numbers
Frequently Asked Questions
What are the types of natural numbers?
The Classification of Numbers: Prime numbers, Composite numbers, Co-Prime Numbers, Perfect numbers, Abundant numbers, Palindromic numbers, even-odd numbers, etc.
What are the symbols of different types of numbers?
The Classification of Numbers: Real Numbers (R), Integers (Z), Natural Numbers (N), Rational Numbers (Q), Irrational Numbers (P), Complex Numbers (C), and Whole Numbers (W).
What is the difference between rational numbers and irrational numbers?
Rational numbers can be expressed in fractional form but irrational numbers can’t.
Zero (0) is a real number or imaginary?
As we know, the square root of a non-positive real number is called an Imaginary number and Zero is neither a negative nor positive, real number. Thus Zero is the Real and Imaginary number.
What are complex numbers?
The numbers which can be expressed in the form of a+ib where a & b are Real Numbers, imaginary unit i=\sqrt{-1}. All real numbers are complex numbers with their imaginary parts equal to zero.
Zero is a rational or irrational number?
Zero can be expressed in the fractional form where the numerator is equal to zero so Zero is a rational number.
𝜋 (pi) is a rational or irrational number?
𝜋 (pi) is an irrational number because its decimal expansion is non-terminating and non-repeating.
What are the properties of 𝜋 (pi)?
𝜋 (pi) is an irrational number, a Real number, a Transcendental number, and a non-algebraic number.
What is a Polynomial?
An expression composed of variables, constants, and exponents, combined with arithmetic operators (+,-,÷,×) is called a Polynomial. The exponents of variables should be in whole numbers.
Classification of Numbers (MCQ)
20 multiple choice questions with solutions on the concepts of Classification of numbers and Simplification:

