Here we would learn about some very special types of numbers, their characteristics, and their usage in arithmetic problems.

Natural Numbers can be further classified into various special types of numbers, the description of which is given below. Click Here for a detailed description of The Classification of Numbers.
Prime Numbers
A natural number (P) greater than 1, which is divisible by only two numbers, One (1) and the number itself (P), is called the Prime Number.
Prime Numbers have exactly two factors which are 1 and the number itself (P=1×P).
Example: 2,3,5,7,11,…. (Types of Numbers)
| Range | Number of Primes |
| 1-50 | 15 |
| 51-100 | 10 |
| 1-1000 | 168 |
| 1-10000 | 1229 |
| 1-100000 | 9592 |
Number of Primes Between 1 to 50:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47 (Total 15 Primes)
Sum=328
Average=\frac{328}{15}=21.8\overline{6}
Number of Primes Between 1 to 100:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97 (Total 25 Primes)
Sum=1060
Average=\frac{1060}{25}=42.4
Facts About Prime Numbers
- Zero (0) and One (1) aren’t Prime numbers because 0 is less than one and 1 doesn’t have two factors.
- 2 is the smallest and only prime number, which is even.
- 2 and 3 are the only prime numbers that are consecutive.
- Every even natural number greater than 2 can be expressed as the sum of two prime numbers.
Example: 12=5+7, 44=31+13, 86=83+3, etc. (Types of Numbers)
- The reciprocal of every prime number (except 2 and 5) is a recurring decimal number.
Example: \frac{1}{3}=0.\overline{3}, \frac{1}{7}=0.\overline{142857}, \frac{1}{11}=0.0\overline{90}, etc. (Types of Numbers)
- If (P-1)! is divided by P, the remainder=-1 or (P-1). Here P, Prime Number, and ! is a factorial sign. (5!=5×4×3×2×1=120)
Example: 6! mod 7=6
22! mod 23=22
Modulo Operation (mod): It returns the remainder after one number is divided by another. Example: 9 mod 3=0, 5 mod 2=1
- Polynomial f(x)=x^{2}+x+41 is Prime, where x\in{W} or x={0,1,2,3,4…}
Example: f(0)=41, f(1)=43, f(2)=47, etc. (Types of Numbers)
- If P is the Prime number greater than 3 (P>3) then P^{2}-1 is always divisible by 24.
Example: 5^{2}-1=24 (Divisible by 24)
7^{2}-1=48 (Divisible by 24)
11^{2}-1=120 (Divisible by 24)
89^{2}-1=7920 (Divisible by 24) -Types of Numbers
Extension: The square of any prime number divided by 24 gives the remainder 1.
Example: 17^{2} mod 24=1, 113^{2} mod 24=1, etc.
- Every prime number greater than 2 always equals the difference between the squares of two consecutive numbers.
Example: 5=3^{2}-2^{2}
41=21^{2}-20^{2}Let’s find these consecutive numbers: (Types of Numbers)
P\times1=a^{2}-b^{2}=(a+b)(a-b).
(a+b)=P.
(a-b)=1.
Add both equations: 2a=P+1 or a=\frac{P+1}{2}
So, b=\frac{P-1}{2}
Example: 73=[\frac{73+1}{2}]^{2}-[\frac{73-1}{2}]^{2}=37^{2}-36^{2}
- A unique 20-digit Prime number: 12345678910987654321. (Types of Numbers)
Check the sequence, first 1-10 is written in increasing then 9-1 in decreasing order.
- All the prime numbers greater than 2, follow the pattern of 4n\pm1, Here n is a Natural number.
In other words, a prime number divided by 4, gives the remainder 1 or -1 (-1+4=3).
Example: 89 mod 4=1
43 mod 4=3
- All the prime numbers except 2 and 3, can be expressed in the form of 6n\pm1, Here n is a Natural number.
In other words, a prime number divided by 6, gives the remainder 1 or -1 (-1+6=5).
Example: 89 mod 6=5
43 mod 6=1
- We know 6n+1 or 6n-1 could be a Prime number (P).
Now, P-1=(6n+1)-1=6n
P+1=(6n-1)+1=6n
This Means either (P+1) or (P-1) should be divisible by 6. (Types of Numbers)

Divisible By 6 or Divisible by 2 and 3: For the divisibility by 2, the number should be even, and for the divisibility by 3, the Sum of the digits of the number should be divisible by 3.
Example 1: P=83 (Prime Number)
Step 1: 83-1=82
P-1 is Even but Digit sum (8+2=10) is not divisible by 3
Step 2: 83+1=84
P+1 is Even and Digit sum (8+4=12) is divisible by 3.
Condition for Prime Number is satisfied. (Types of Numbers)
Example 2: P=113 (Prime Number)
Step 1: 113-1=112
P-1 is Even but Digit sum (1+1+2=4) is not divisible by 3
Step 2: 113+1=114
P+1 is Even and Digit sum (1+1+4=6) is divisible by 3.
Condition for Prime Number is satisfied. (Types of Numbers)
Fermat’s Little Theorem
If P is a Prime number and a is a Natural Number such that ‘a’ is not divisible by P then a^{P-1} divided by P gives a remainder equal to 1. (a^{P-1} mod P=1)
Example: 5^{6} mod 7=1
13^{70} mod 71=1
Check whether a number is Prime or Not
First, check whether the number is divisible by 2,3 and 5
Divisibility rule of 2: The unit digit should be even (0,2,4,6,8)
Divisibility rule of 3: The sum of the digits should be divisible by 3.
Divisibility rule of 5: The unit digit should be 0 or 5.
After these steps, the next step should be initiated.
Case 1: Small Number (<1000)
Example 1: Check, whether 83 is a Prime number or not.
Step 1: Find the value of n, here n^{2}\ge83
n=10
Step 2: Write down all Prime numbers less than or equal to 10
2,3,5,7
Step 3: If 83 is not divisible by any of the given prime numbers (2,3,5,7) then it’s a Prime number.
Since 83 is not divisible by 2,3,5 and 7. So, it’s a Prime number. (Types of Numbers)
Example 2: Check, whether 869 is a Prime number or not.
Step 1: n^{2}\ge869 then n=30
Step 2: Prime numbers \ge 30: 2,3,5,7,11,13,17,19,23,29
Step 3: 869 is divisible by 11
So, it’s not a Prime number. (Types of Numbers)
Case 2: Large Number (>1000)
Example (1): Which number is not a Prime number? (Types of Numbers)
- 19001
- 10993
- 25751
- 12387 (Correct)
Rule 1: Except for 2 and 5, the unit digit of all prime numbers could be only 1,3,7, or 9.
Every option could be a potential Prime number.
Rule 2: The remainder, when a prime number is divided by 4 is equal to 1 or 3
(4n \pm 1) rule.
Note: To check the remainder, when a number is divided by 4, just apply division on the last two digits of the number instead of the whole.
- 01 mod 4=1, (b) 93 mod 4=1, (c) 51 mod 4=3, (d) 87 mod 4=3
Every option could be a potential Prime number.
Rule 3: Refer to fact number 13
(a) 19001
P+1 is even and its digit sum (1+9+0+0+2=12) is divisible by 3
It could be Prime.
(b) 10993
P+1 is even and its digit sum (1+0+9+9+4=23) is not divisible by 3
P-1 is even and its digit sum (1+0+9+9+2=21) is divisible by 3
It could be Prime.
(c) 25751
P+1 is even and its digit sum (2+5+7+5+2=21) is divisible by 3
It could be Prime.
(d) 12387
P+1 is even and its digit sum (1+2+3+8+8=22) is not divisible by 3
P-1 is even and its digit sum (1+2+3+8+6=20) is not divisible by 3
It is definitely not a Prime number. (Types of Numbers)
Example (2): Which number is a Prime number?
- 144711
- 144723
- 144765
- 144757 (Correct)
Option (a), (b), and (c) should be eliminated because all are divisible by 3. So, option (d) is an obvious answer.
This is just Luck but in other cases given steps should be followed.
Rule 1: Except for 2 and 5, the unit digit of all prime numbers could be only 1,3,7 or 9
Eliminate option(c)
Rule 2: The remainder, when a prime number is divided by 4 is equal to 1 or 3.
Options a,b, and d qualified
Rule 3: Refer to fact number 13
# Digit sum of a=18
18+1=19 No
18-1=17 No (Disqualified)
# Digit sum of b=21
21+1=22 No
21-1=20 No (Disqualified)
# Digit sum of d=28
28+1=29 No
28-1=27 Yes (Qualified) -Types of Numbers
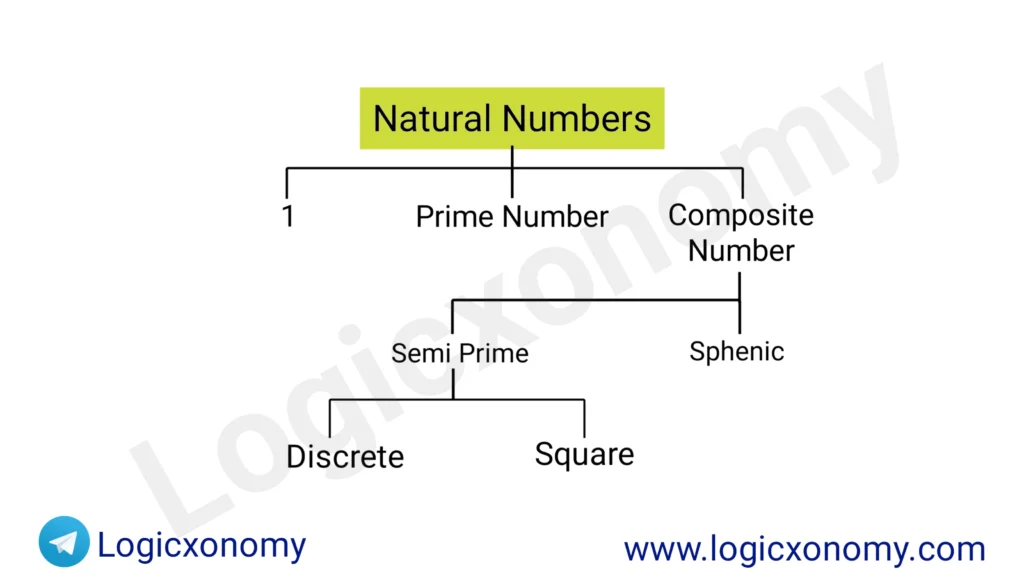
Composite Numbers
Every natural number except 1, which is not a Prime Number is called Composite Number. A composite number has more than two factors.
1 is neither a Prime number nor a Composite number because it has only one factor which is 1 itself.
Example: 4,6,8,9,10,12,14…
Some Facts about Composite Numbers:
- 4 is the smallest composite number.
- Composite numbers have more than two factors.
Que: Check whether 457 is a composite number or not.
Solution: First check whether 457 is a Prime or not. If it’s not a Prime number then obviously it’s a composite number.
Step 1: n^{2} \ge 457 then n=22
Step 2: Prime numbers (\leq22) are 2,3,5,7,11,13,17,19
Step 3: 457 is not divisible by any of the given Prime numbers so it’s a Prime Number or 457 is not a composite number.
Types of Composite Numbers
Composite numbers are of two types.
- Semi-Prime numbers
- Sphenic Numbers
1. Semi-Prime Numbers: The product of exactly two Prime numbers is called Semi-Prime. These two prime numbers could be equal or different. Semi Prime numbers are further classified into Discrete and Square Semi-Prime numbers.
Example: 35=5×7 (Discrete or Distinct Semi-Prime)
143=11×13 (Discrete or Distinct Semi-Prime)
6=3×2 (Discrete or Distinct Semi-Prime)
289=17×17=17^{2} (Square Semi-Prime)
121=11×11=11^{2} (Square Semi-Prime)
2. Sphenic Numbers: A product of three distinct Prime numbers (Square free) is called a Sphenic Number.
Example: 30=2×3×5
42=2×3×7
114=2×3×19
Note: The number which is not divisible by any perfect square is called Square free number.
Example: 18 is not a square-free number because 18=2\times3^{2}.
Highly Composite Number
If a composite number has more divisors than any other number less than itself then it’s a Highly Composite Number. Highly composite numbers are also known as Anti-Prime Numbers.
Example: 4, 6, 12, 24, 36, 48, 60…..
| Number | No. of Divisors | Divisors |
| 4 | 3 | 1,2,4 |
| 6 | 4 | 1,2,3,6 |
| 12 | 6 | 1,2,3,4,6,12 |
| 24 | 8 | 1,2,3,4,6,8,12,24 |
| 36 | 9 | 1,2,3,4,6,9,12,18,36 |
| 48 | 10 | 1,2,3,4,6,8,12,16,24,48 |
| 60 | 12 | 1,2,3,4,5,6,10,12,15,20,30,60 |
Find the Number of Divisors of any number:
If N=2^{a}\times3^{b}\times5^{c}\times7^{d}... (Prime factorization)
Then the number of factors=(a+1)×(b+1)×(c+1)×(d+1)×….
Example: (i) Find the number of divisors of 36.
36=2^{2}\times3^{2}Number of factors=(2+1)×(2+1)=9
(ii) Find the number of divisors of 60.
60=2^{2}\times3^{1}\times5^{1}Number of factors=(2+1)×(1+1)×(1+1)=12
Co-Prime Numbers
A pair of numbers having HCF (Highest common Divisor) equal to 1 are called Co-Prime Numbers. Co-Prime numbers are also referred to as relatively Prime numbers. Any two consecutive natural numbers will always be Co-Prime numbers.
a and b are Co-Prime if HCF(a,b)=1
Here a or b need not be a Prime number.
Example: (15,22), (8,21), (1,15), etc.
Twin Primes: A pair of prime numbers in which the difference of numbers is equal to 2 is called a twin prime.
Example: (3,5), (5,7), (17,19), (29,31), etc.
Mersenne Prime Numbers
A Prime number in the form 2^{n}-1, where n is also a prime number is called a Mersenne Prime. As of September 2022, there are 51 Mersenne Prime are known.
It is not necessary that for all prime n, there would be a Mersennary Prime to exist.
| n (Prime) | 2^{n}-1 | Prime? |
| 2 | 3 | Yes |
| 3 | 7 | Yes |
| 5 | 31 | Yes |
| 7 | 127 | Yes |
| 11 | 2047 | No (Divisible by 23) |
| 13 | 8191 | Yes |
Perfect Numbers
A number that is equal to the sum of its all proper divisors is called a Perfect Number.
Example: 28=1+2+4+7+14

Proper Divisors: The divisors of any natural number (N) which are less than N, are called its proper divisors.
Example: Proper divisors of 12 are 1,2,3,4,6
Note: Here 12 is not included. (Types of Numbers)
All divisors of 12 are 1,2,3,4,6,12
Proper divisors of 12 are 1,2,3,4,6
Find a Perfect Number
Perfect numbers always follow a definite pattern. (Types of Numbers)
G.P. (Geometric progression) Series: 2^{0}, 2^{1}, 2^{2}, 2^{3}, 2^{4}, ... ,2^{n-1}.
The sum of the G.P. Series= 2^{0}+ 2^{1}+ 2^{2}+ 2^{3}+ 2^{4}+ ... +2^{n-1}=2^{n}-1.
If the sum of the first n terms (n is a Prime Number) of this GP series is a Prime number then (2^{n}-1)\times(2^{n-1}) would be the Perfect Number.
Here, (2^{n}-1) is a Mersenne Prime, and (2^{n-1}) is the last term of the series.
| n (Prime Number) | Mersenne Prime (2^{n}-1) | Perfect Number (2^{n}-1)\times(2^{n-1}) | Sum of Proper Divisors |
| 2 | 3 | 3×2=6 | 1+2+3=6 |
| 3 | 7 | 7×4=28 | 1+2+4+7+14=28 |
| 5 | 31 | 31×16=496 | 1+2+4+8+16+31+62+124+248=496 |
| 7 | 127 | 127×64=8128 | —– |
| 13 | 8191 | 8191×4096=33550336 | —– |
Facts About Perfect Numbers:
- All perfect numbers are even.
- There is no odd perfect number in existence till now.
- The Sum of the reciprocals of all the divisors of the perfect number is equal to two (2).
Example: (i) Divisors of 6 are 1,2,3,6
The Sum of reciprocals=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=\frac{6+3+2+1}{6}=2.
(ii) Divisors of 28 are 1,2,4,7,14,28
The Sum of reciprocals=\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{7}+\frac{1}{14}+\frac{1}{28}=\frac{28+14+7+4+2+1}{28}=2.
- Perfect Numbers are half of the sum of all their divisors.
Example: Sum of all divisors of 6=1+2+3+6=12
The sum of all divisors of 28=1+2+4+7+14+28=56
Deficient Numbers
A number that is greater than the sum of all its proper divisors is called a Deficient Number.
Example: 1,2,3,4,5,7,8,9,10,11,13,14,15,16,17,19, etc. (Types of Numbers)
4 > Sum of proper divisors (1+2=3)
15> Sum of proper divisors (1+3+5=9)
All prime numbers are deficient numbers because Prime Numbers have only one proper divisor which is 1.
Abundant Numbers
A number that is less than the sum of all its proper divisors is called an Abundant Number.
Example: 12,18,20,24,30,36,40,42,48,54,56,60,66,70,72,78,80,84,88,90,96,100, etc.
12< Sum of proper divisors (1+2+3+4+6=16)
54< Sum of proper divisors (1+2+3+6+9+18+27=66)
Facts about Abundant Numbers: (Types of Numbers)
- 12 is the first (Smallest) Abundant Number.
- There are 22 Abundant Numbers from 1 to 100 and all are even. It doesn’t mean all abundant numbers are even.
- Some odd Abundant numbers are 945, 1575, 2205, 2835, etc. So we can say 945 is the smallest and first odd Abundant Number.
- Every multiple of an Abundant number is also an Abundant Number.
- Roughly one-fourth of the natural numbers are Abundant Numbers.
The Numbers from 1 to 100: (Types of Numbers)
| Type of Numbers | Total Counting |
| Deficient Numbers | 76 |
| Perfect Numbers | 2 |
| Abundant Numbers | 22 |
Amicable Numbers
Two numbers are Amicable if the sum of all proper divisors of one number is equal to the other number.
Example: (220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368), etc.
The Sum of proper divisors of 220 =1+2+4+5+10+11+20+22+44+55+110=284
The Sum of proper divisors of 284 =1+2+4+71+142=220
Happy Numbers
Let, a number be repeatedly replaced by the sum of the squares of its digits until the result ends in a single digit.
If the final result is 1, such a number is called a Happy Number and in case of a different result, the number is called an Unhappy or Sad Number.
Examples: 1,7,10,13,19,23,28,31,32,44, etc.
There are 20 Happy numbers from 1 to 100.
(i) Check, whether 19 is a Happy number or not.
1^{2}+9^{2}=82.
8^{2}+2^{2}=68.
6^{2}+8^{2}=100.
1^{2}+0^{2}+0^{2}=1 (Final result=1)
19 is a Happy number.
(ii) Check, whether 25 is a Happy number or not.
2^{2}+5^{2}=29.
2^{2}+9^{2}=85.
8^{2}+5^{2}=89.
8^{2}+9^{2}=145.
1^{2}+4^{2}+5^{2}=42.
4^{2}+2^{2}=20.
2^{2}+0^{2}=4.
So, 25 is an Unhappy or Sad Number.
Narcissistic or Armstrong Numbers
If an n-digit number is equal to the sum of the nth powers of its digits then it is called a Narcissistic or Armstrong Number.
Example: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, etc.
(i) Check, whether 1634 is an Armstrong number or not.
1^{4}+6^{4}+3^{4}+4^{4}=16341634 is an Armstrong Number.
(ii) Check, whether 153 is an Armstrong number or not.
1^{3}+5^{3}+3^{3}=153153 is an Armstrong Number.
Palindromic Numbers
If the value of a number does not change when the digits are reversed, it is called a Palindromic number.
Example: 11, 272, 457754, etc. (Types of Numbers)
Fermat Numbers
If 2^{2^{n}}+1 is a Prime number, where n is a Whole Number (0,1,2,3,4….) then it is called a Fermat Number or Fermat Prime.
| n | 2^{2^{n}}+1 | Fermat Prime? |
| 0 | 3 | Yes |
| 1 | 5 | Yes |
| 2 | 17 | Yes |
| 3 | 257 | Yes |
| 4 | 65537 | Yes |
| 5 | 4294967297 | No (Divisible by 641) |
Types of Numbers (FAQ)
What is the average of all Prime numbers below 100?
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97 (Total 25 Primes)
Sum=1060
Average=\frac{1060}{25}=42.4What is the median of the first 10 prime numbers?
Ten prime numbers in ascending order: 2,3,5,7,11,13,17,19,23,29
Median= Average of 5th and 6th term (middle value)
=\frac{11+13}{2}=12Find the number of factors of P² if P is a Prime number?
P=1\times P
So, factors of P^{2} are 1, P, P^{2} (3 factors)
Number of factors of P^{n} = n+1Are 0 and 1 Prime numbers?
The prime number should be a Natural number greater than 1 which can be divisible by only 1 and itself. By this definition 0 and 1 are not Prime Numbers.
How to find whether a number is Prime or Not?
Let, we have to find out whether 727 is a prime or not.
Step 1: Find the smallest value of n, where n^{2}\ge727
n=27
Step 2: Prime numbers (\leq27): 2,3,5,7,11,13,17,19,23
Step 3: Check whether 727 is divisible by any of the given prime numbers or not.
Not divisible.
So, we can say 727 is a Prime number.Can negative numbers be Prime numbers?
No, the Definition of the prime number restricted it to be a positive number above 1.
Do odd perfect numbers exist?
There is no odd perfect number that can be found till now. Surprisingly all perfect numbers are even numbers.
What is the formula for Prime numbers?
There is no such formula to find prime numbers because Prime numbers never follow any specific pattern but there are some formulas that are true for prime numbers.
1. x^{2}+x+41 is Prime, where x\in{W} or x={0,1,2,3,4…}
2. 2^{n}-1, where n is also a prime number is called a Mersenne Prime. This formula is true in 99% of cases means not true for all prime values of n.
Example: For n=11, 2^{n}-1=2047 (It is divisible by 23)What is the formula for Perfect numbers?
If 2^{n}-1 is a prime number, where n is also a Prime number then (2^{n}-1)\times(2^{n-1}) will be the Perfect number.
What are Anti-Prime numbers?
Anti-Prime numbers or Highly composite numbers are those numbers that have more divisors than any other number less than itself.
Example: 4, 6, 12, 24, 36,etc.
Types of Numbers (MCQ)
20 MCQ based on the Types of Numbers:

