In this chapter, we will learn some powerful Geometry Basics and their practical applications. Geometry is a branch of Mathematics that deals with the study (Measurements) of shapes that can be seen everywhere in our everyday life like points, lines, polygons, spheres, cones, cylinders, pyramids, prisms, etc.
‘Geometry’ is derived from two Greek words – ‘Geo’ means ‘Earth’ and ‘Metron’ means ‘Measurement’.
Geometry is classified into two parts: Plane geometry (2D) and Solid Geometry (3D)
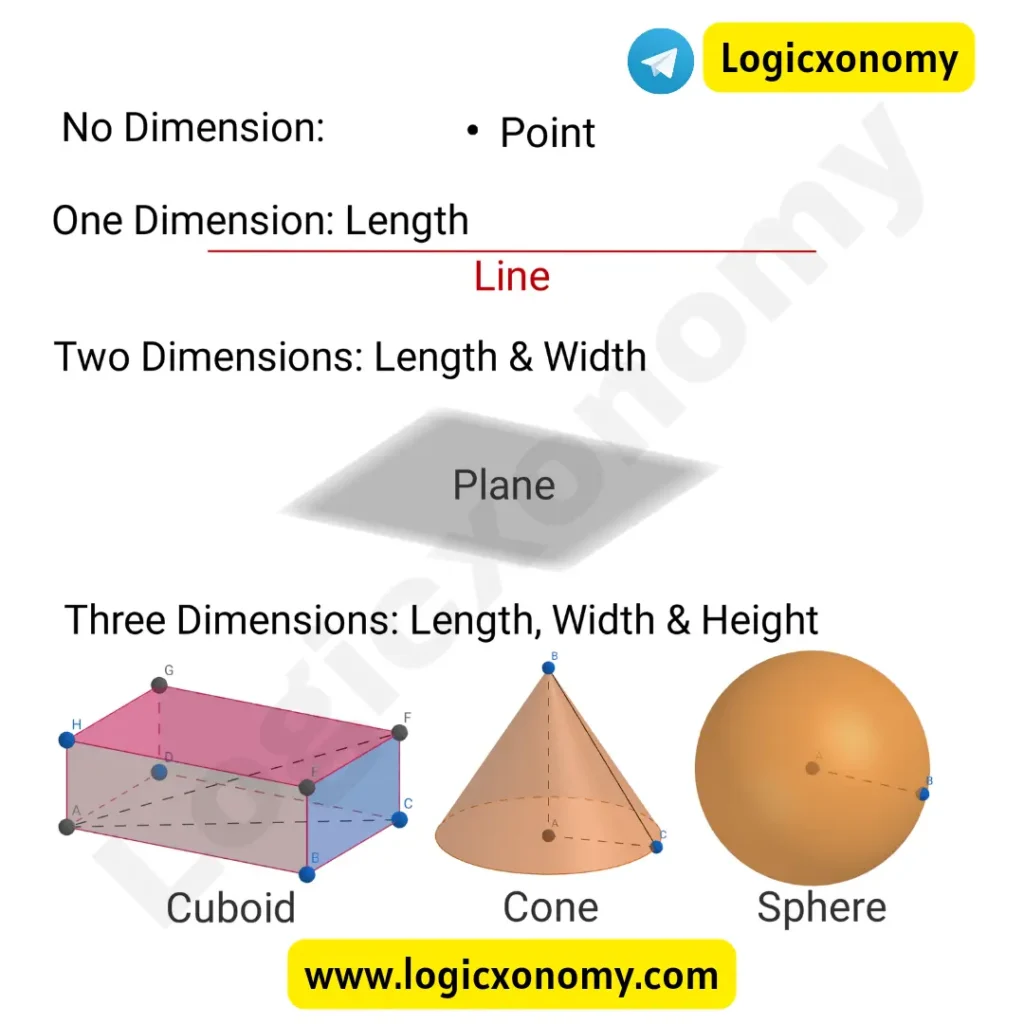
Plane Geometry: In 2D or Plane Geometry, we study the length, area, and perimeter of two-dimensional shapes (triangles, quadrilaterals, polygons, circles, etc.) that can be drawn on paper.
Solid Geometry: In 3D geometry, we study the surface areas, volumes, and heights of three-dimensional shapes. 3D shapes (Cone, Cylinder, Cuboid, Pyramid, Sphere, etc.) can not be drawn on paper. (Geometry Basics)
Basic concepts of Geometry
- Point: The point has no length, breadth, or height (Zero Dimensional). It is an exact location in space, represented by a dot sign. (Geometry Basics)
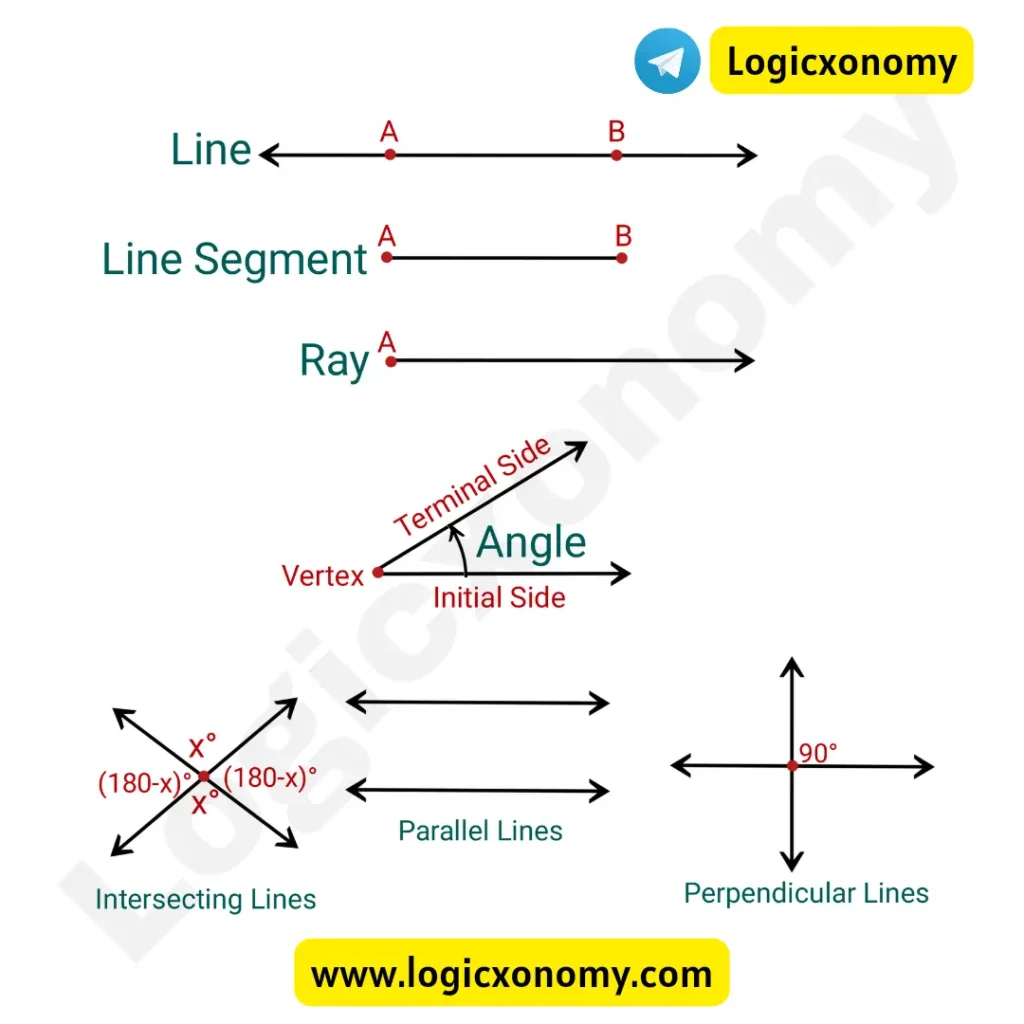
- Line: A line is a collection of collinear points that extends in opposite directions endlessly. It’s a one-dimensional figure which has no thickness.
- Line Segment: A part of the line with two endpoints.
- Ray: It has a starting point but no endpoint means a ray extends infinitely in one direction.
- Angle: Two rays or lines with the same starting point form an Angle.
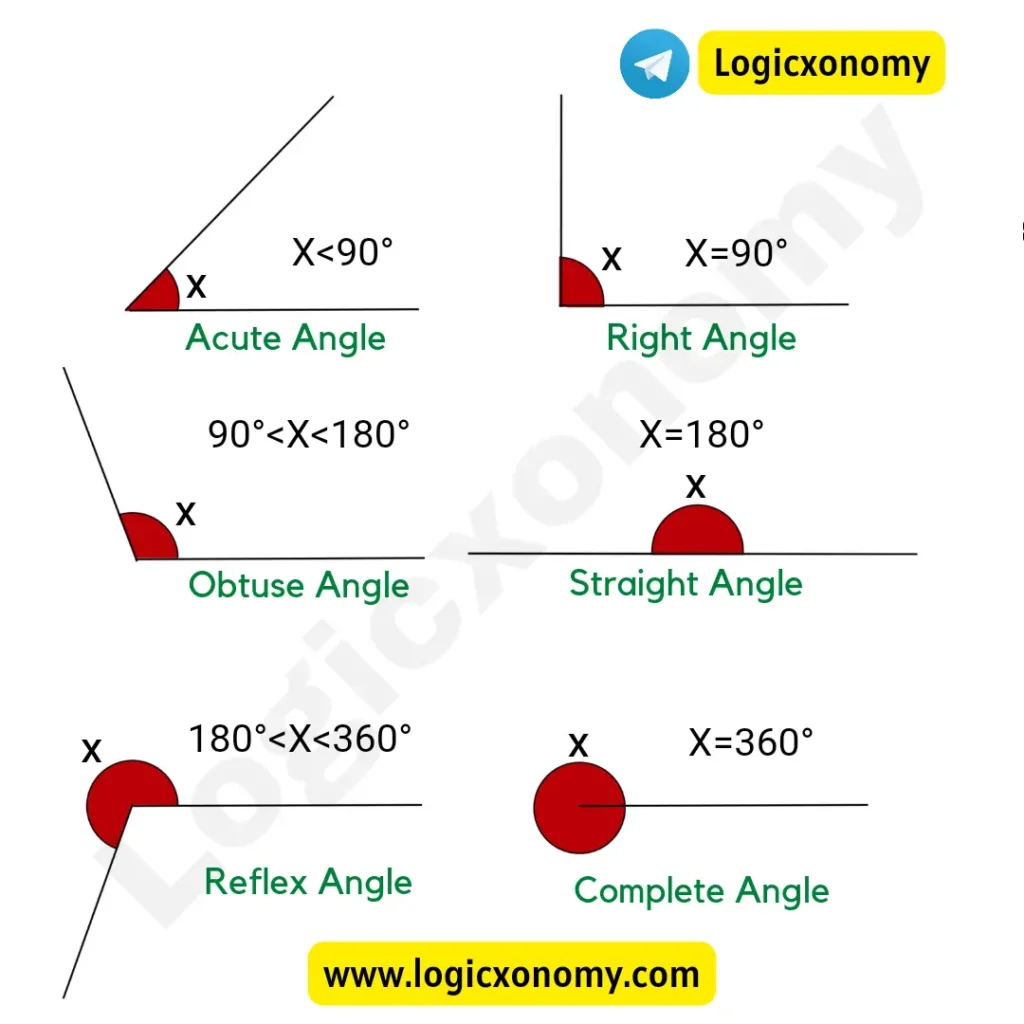
There are six types of Angles: (Geometry Basics)
- Acute Angle: Less than 90°
- Right Angle: Equal to 90°
- Obtuse Angle: Greater than 90° but less than 180°
- Straight Angle: Equal to 180°
- Reflex Angle: Greater than 180° but less than 360°
- Complete Angle: Equal to 360°
Pair of Lines: A pair of lines can form Intersecting lines, Perpendicular lines, Parallel lines, and Skew lines. (Geometry Basics)
- Intersecting lines: These lines cross each other at a point (Point of Intersection).
- Perpendicular lines: The intersecting lines that form a 90° angle at the point of intersection, are called perpendicular lines.
- Parallel lines: When two lines, drawn in the same plane, never cross each other or are always at the same distance apart.
- Skew lines: Skew lines can not be drawn on paper because both lie in different planes. Two lines that lie on different planes neither intersect nor parallel each other. Skew lines can exist only in three or more dimensions.
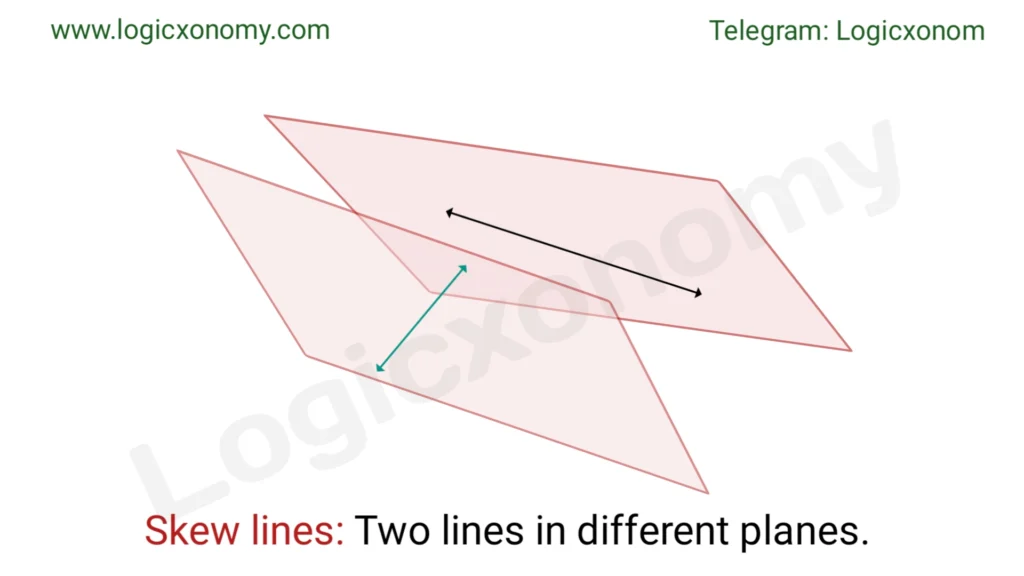
- Plane: The plane is a two-dimensional flat surface that extends infinitely in all directions. It has a length and width but not a height. All lines and points which lie on the same plane are called coplanar. Two coplanar lines either intersect or are parallel.
Pair of Angles: Complementary angles and Supplementary angles. (Geometry Basics)
When the sum of two angles is equal to 90° then they are called Complementary angles.
Example: If x=50° and y=40° then x and y are Complementary Angles.
When the sum of two angles is equal to 180° then they are called Supplementary angles.
Example: If x=70° and y=110° then x and y are Supplementary Angles.
Concept of Degree, Minute, and Second
1°=60’ (60 Minutes)
1’=60’’ (60 seconds)
So, 180°=179°60’
=179°59’60’’
90°=89°60’
=89°59’60’’
Que: Find the complementary angle of 35°18’27’’.
Solution: Complementary Angle= 90°-35°18’27’’
=89°59’60’’ – 35°18’27’’
=54°41’33’’
Que: Find the Supplementary angle of 35°18’27’’.
Solution: Supplementary Angle= 180°-35°18’27’’
=179°59’60’’ – 35°18’27’’
=144°41’33’’
Radian and Steradian
Radian: The value of the angle subtended by an arc of the length equal to the radius of the circle, at the center of the circle, is 1 radian (1c).
It is the standard unit of angle in the International System of Units (SI).
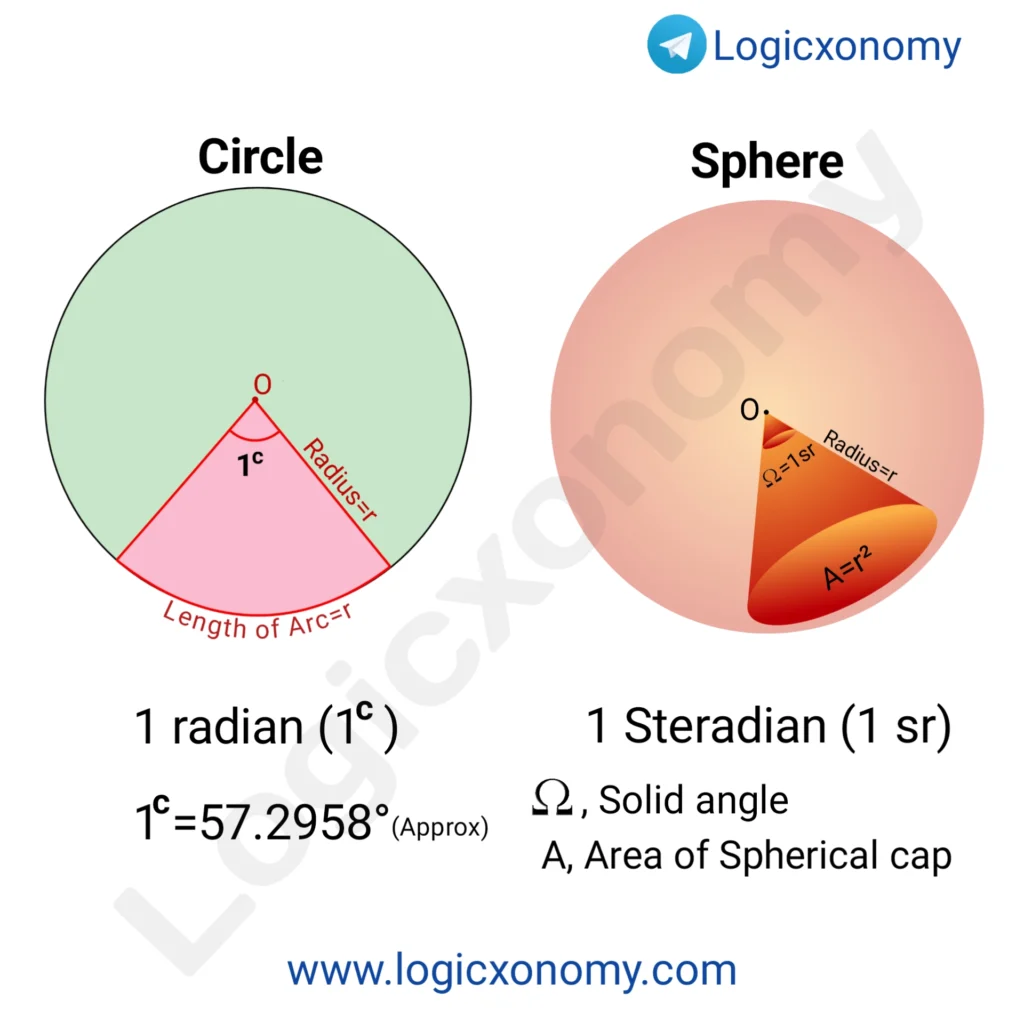
Let, θ is the angle subtended by an arc of the circle at its center. (Geometry Basics)
Then, \frac{360°}{1^{c}}=\frac{C}{L}=\frac{2\pi r}{r}.
Circumference of the Circle (C)=2𝜋r
Length of Arc (L)=r
1^{c}=\frac{180°}{\pi} or \pi^{c}=180°
1c=57.2958° (Approximately)
1°= 0.0174533c (Approximately)
There is one more formula to find the angle subtended at the center of the circle by an arc.
\Theta=\frac{s}{r}Here \Theta is in radian
s, length of the arc
r, length of the radius of the circle
Steradian: The value of a solid angle subtended by a part of the surface, of area equal to the square of the radius of the Sphere, at the center of the Sphere, is 1 Steradian (1 sr ).
Solid Angle Ω=\frac{A}{r^{2}}=\frac{r^{2}}{r^{2}}=1 sr.
The entire sphere has a solid angle of 4𝜋.

Parallel Lines
In the figure, AB∥CD, and LM is a Transversal line intersecting AB and CD at P and Q respectively.
When a transversal line crosses two parallel lines then four types of angles are formed: Adjacent angles, Corresponding angles, Alternate angles, and Vertically Opposite angles.

- Corresponding Angles: The pair of angles that holds the same relative positions is called Corresponding angles.
Example: ∠1=∠5, ∠2=∠6, etc. (Geometry Basics)
- Vertically Opposite Angles: A pair of opposite angles at the point of intersection of two intersecting lines are called vertically opposite angles.
Example: ∠1=∠3, ∠2=∠4 (Here the line AB is intersecting LM)
- Alternate Angles: When a transversal line crosses two parallel lines, the two angles (at different points of intersection) that make a ‘Z’ pattern are called Alternate angles.
Example: ∠1=∠7, ∠3=∠5, etc.
- Adjacent Angles: Two angles that share the same vertex and a common side are called Adjacent angles.
Example: ∠1 and ∠2, ∠5 and ∠8, etc. (Geometry Basics)
Que: Find the value of ∠PRQ, if PR and QR are the angle bisectors of ∠QPB and ∠PQD.
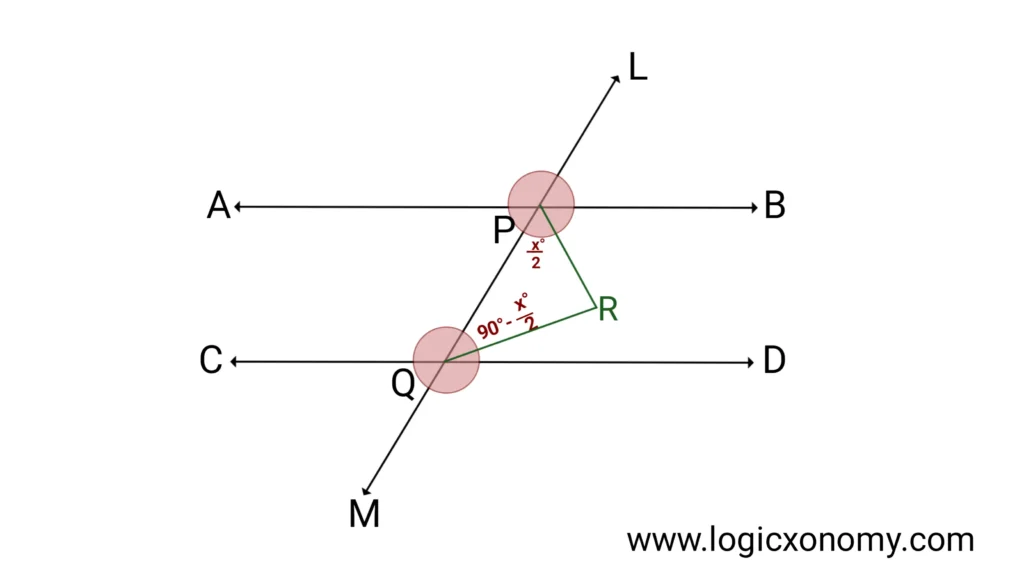
Solution: Let, ∠QPB=x° then ∠PQD=(180-x)°
∠RPQ=\frac{x°}{2}
∠RQP=\frac{(180-x)°}{2}
In \triangle PRQ, the Sum of all internal angles=180°
\frac{x°}{2}+\frac{(180-x)°}{2}+∠PRQ=180°
∠PRQ=90°
Parallel and Transversal lines
In the given figure AB∥CD∥EF∥GH, are intersected by two transversal lines.
Transversal Line: A line that crosses more than one coplanar line is called a Transversal line.
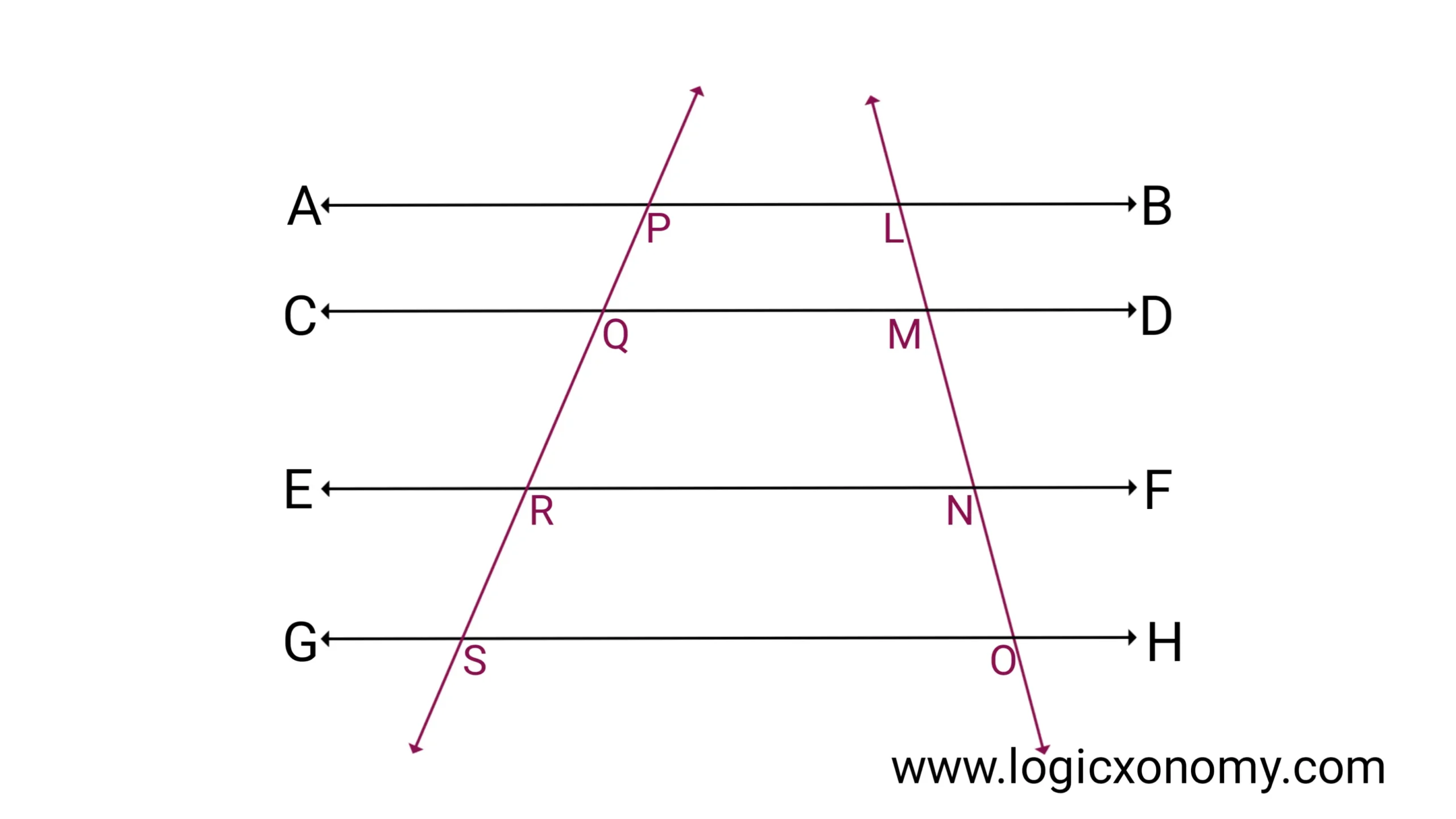
Then, PQ : QR : RS = LM : MN : NO
Triangle
The triangle is a shape enclosed by three line segments. It has three sides and three interior angles, where the sum of all internal angles is 180°. (Geometry Basics)
Property 1:
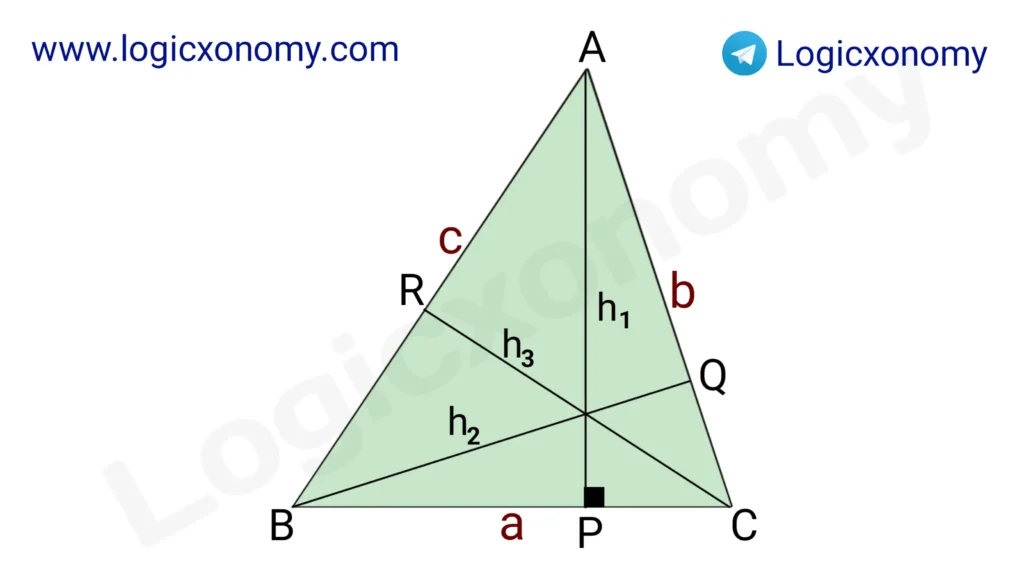
Area of △ABC= \frac{1}{2}\times Base \times Height
\frac{1}{2}\times ah_{1}=\frac{1}{2} \times bh_{2}=\frac{1}{2}\times ch_{3}Divide the equation by a×b×c
\frac{h_{1}}{bc}=\frac{h_{2}}{ca}=\frac{h_{3}}{ab}So, h1: h2: h3=bc : ca : ab
In the given figure there are three triangles △ACB, △ADB, and △AEB placed on the same base AB and between two parallel lines AB and DE. (Geometry Basics)
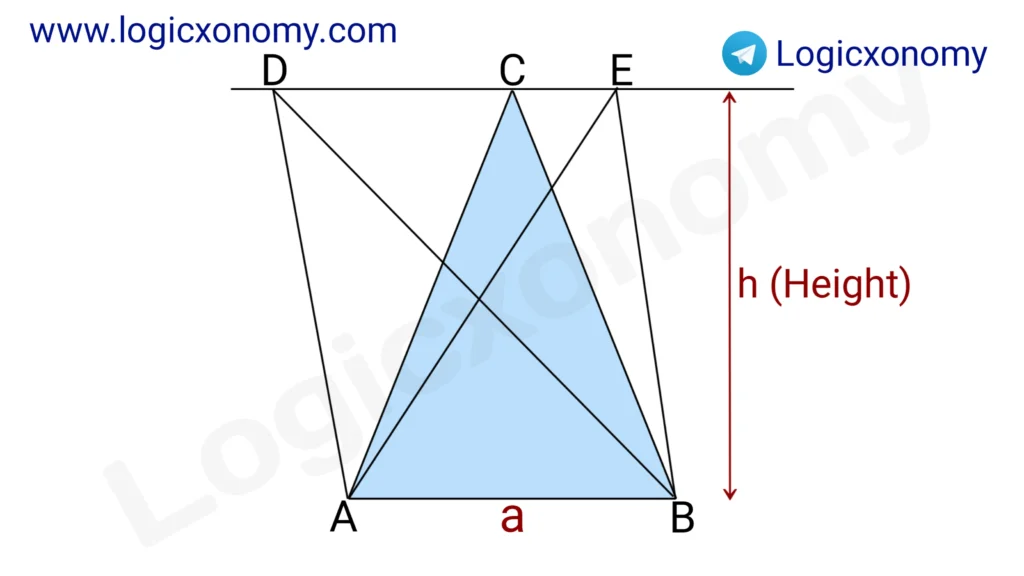
In such cases, ar △ACB=ar △ADB=ar △AEB
Here, the Base and Height are the same.
Property 2: Sine Formula of Area, Cosine Formula, and The Sine Rule. (Geometry Basics)
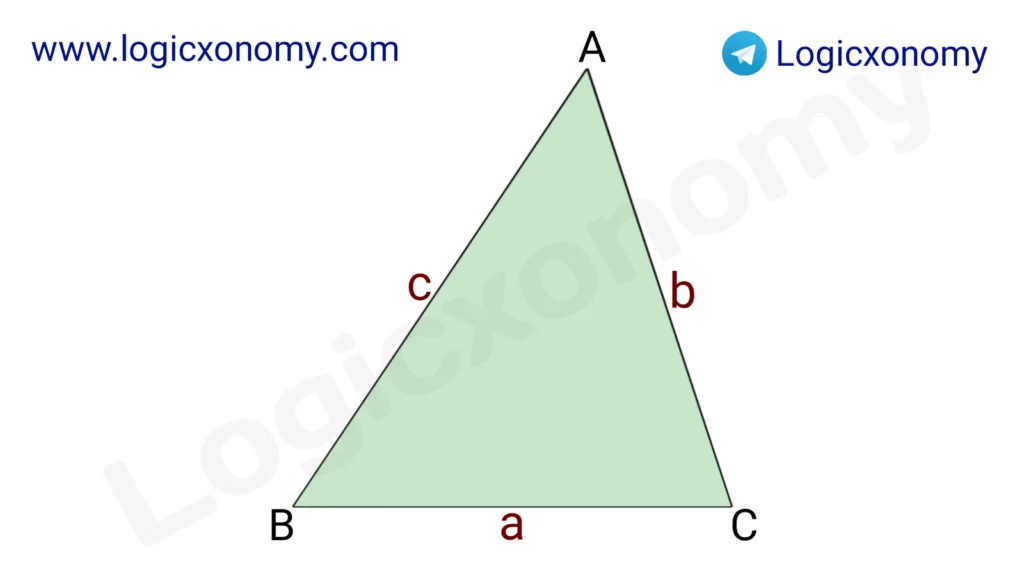
Sine Formula of Area:
Area of △ABC=\frac{1}{2}\times bc\times Sin(A) =\frac{1}{2}\times ca\times Sin(B)=\frac{1}{2} ab\times Sin(C).
Cosine Formula:
Cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}
Cos B=\frac{c^{2}+a^{2}-b^{2}}{2ca}
Cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab} ……….(i)
a=b Cos(C)+c Cos(B)
b=c Cos(A)+a Cos(C)
c=a Cos(B)+b Cos(A) ………..(ii)
Sine Rule:
\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}=2R.
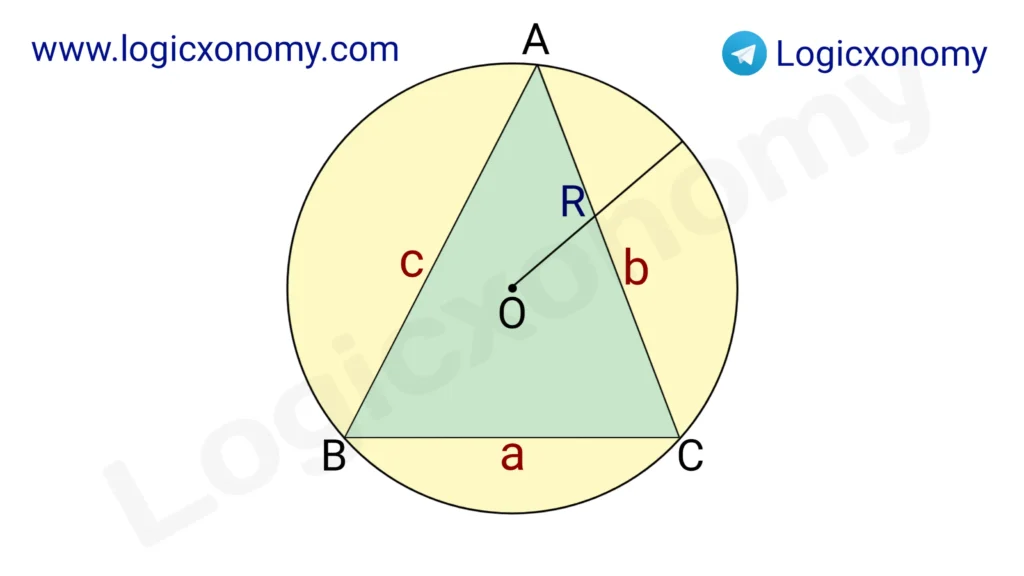
Here, R is the length of the Circumradius of △ABC.
Property 3: The ratio of Base and Area
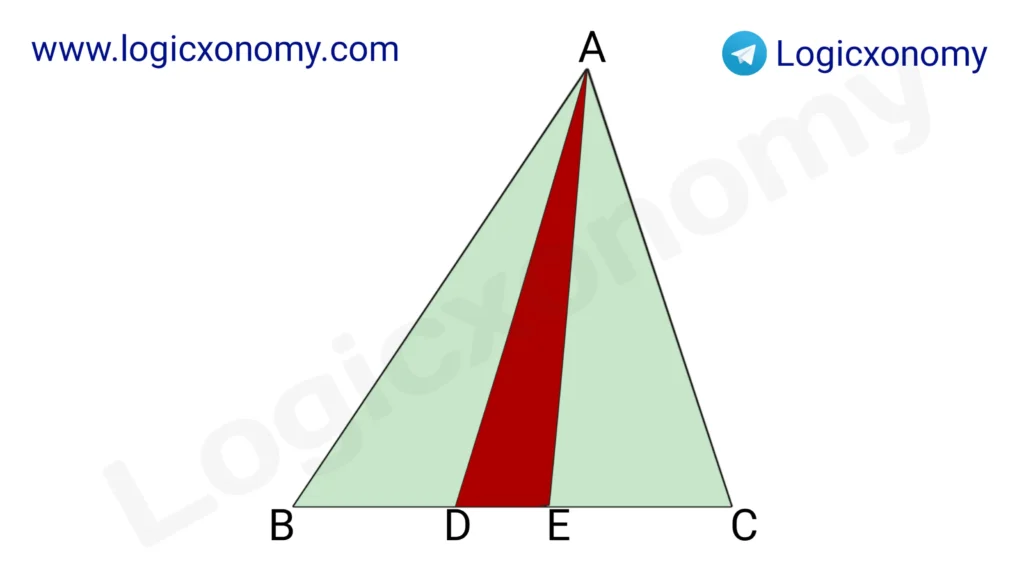
Area of △BAD : Area of △DAE : Area of △EAC= BD : DE : EC
Property 4: External Angle of the triangle
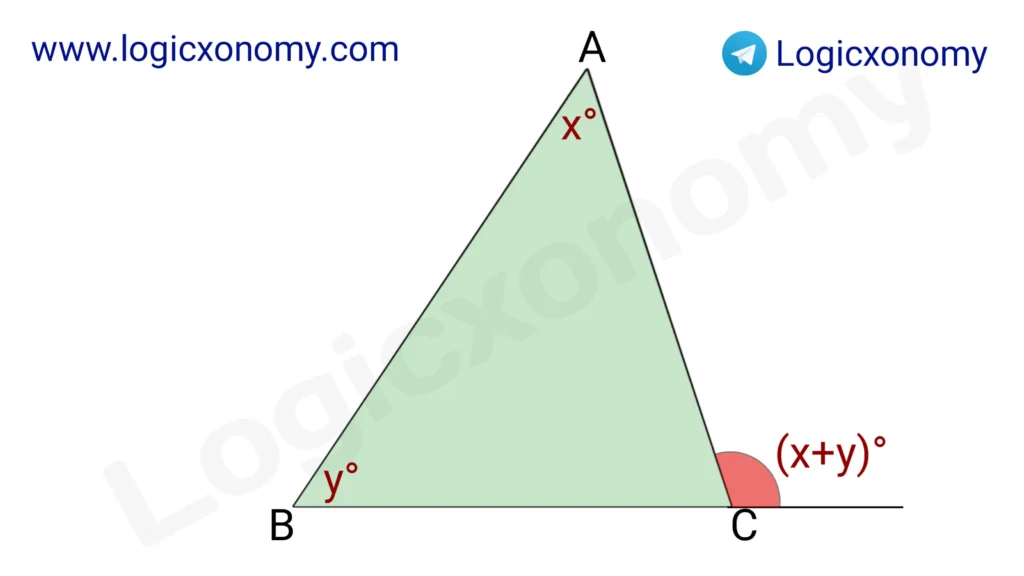
The External angle of the triangle is equal to the Sum of two opposite internal angles.
Property 5: The ratio of the sides of a Right angle triangle.
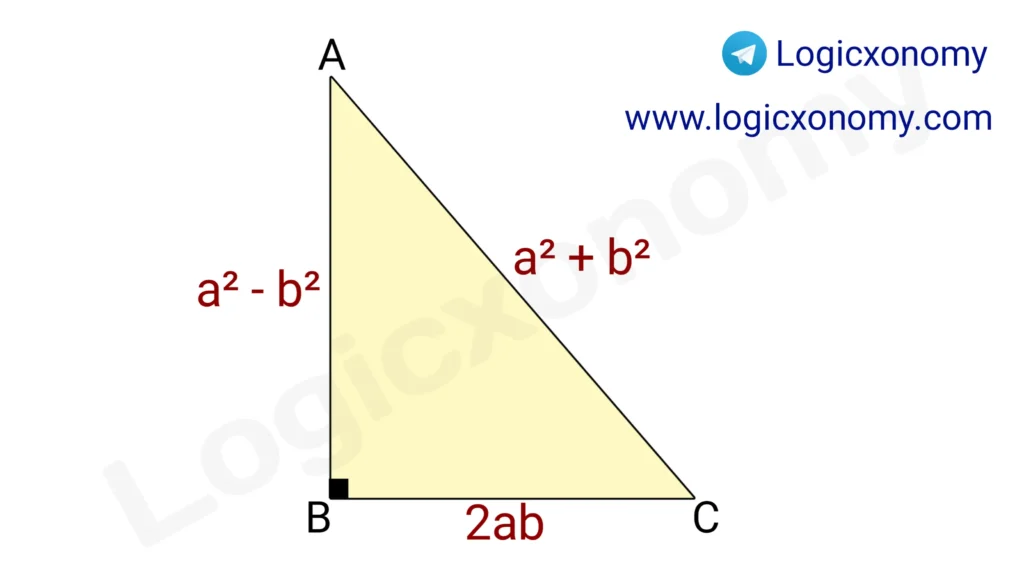
Here a and b are the natural numbers.
Property 6: Area of the triangle when coordinates of the vertices are given.
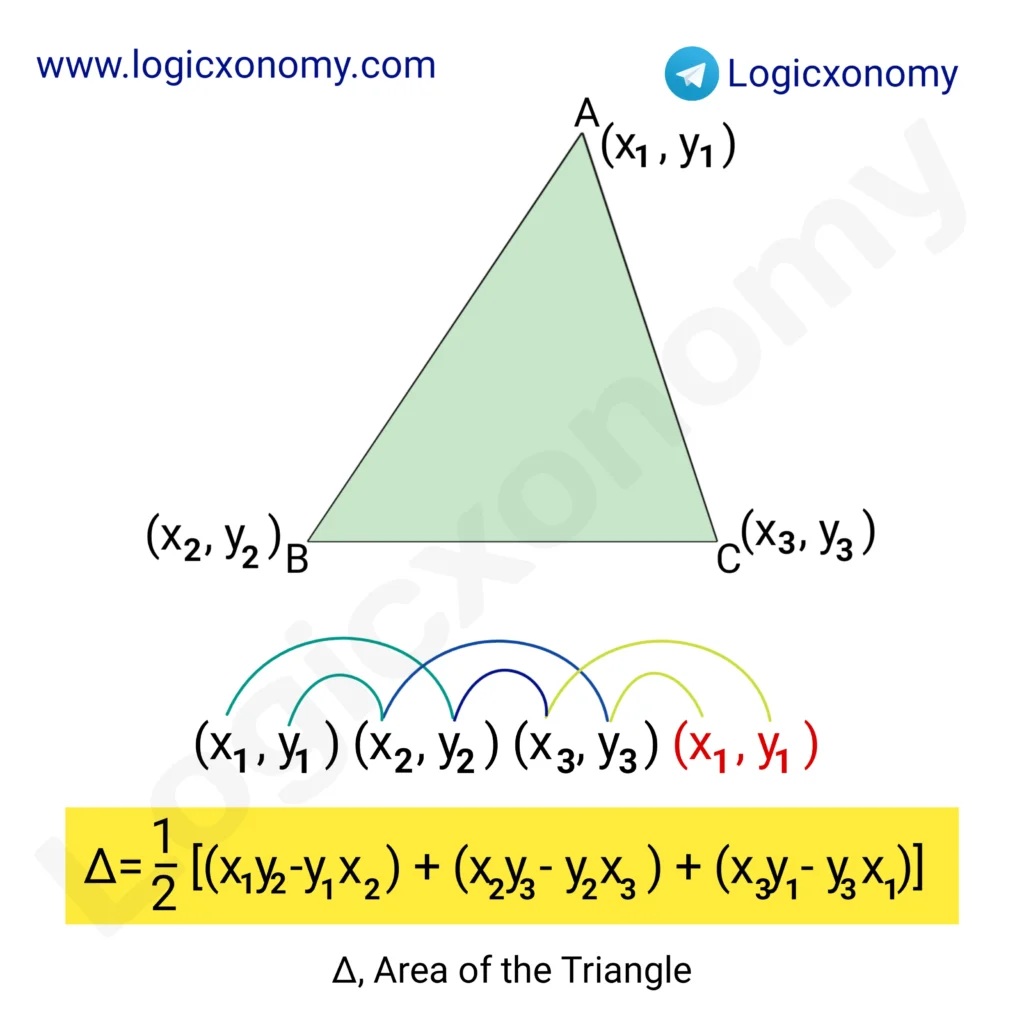
Let the coordinates of the vertices of the triangle be (-2,3), (4,5), and (0,6) then find the area of the triangle.
(-2,3), (4,5), (0,6), (-2,3)
Area=\frac{1}{2}[(-2\times 5-4\times 3)+(4\times 6-5\times 0)+(0\times 3-6\times (-2))].
=\frac{1}{2}[-22+24+12]
=\frac{1}{2}\times 14
=7 square unit
Pedal Triangle and Orthic Triangle: Click Here
Property 7: Area of any polygon, when coordinates of the vertices are given.
The same (given above) procedure should be followed in each case.

Polygon
A closed two-dimensional shape, formed by more than two lines is called Polygon. The word Polygon is derived from two Greek words: ‘Polus’ means ‘Many’ and ‘Gonia’ means ‘Angle or Corner’.

Types of Polygon
(i) Regular and Irregular Polygon: All Angles and Sides of a Regular Polygon are equal. In the case of different side lengths or Angles, it is an Irregular Polygon. (Geometry Basics)

(ii) Convex and Concave Polygon: All internal angles of a convex polygon are always less than 180°, while in a Concave Polygon, at least one internal angle should be greater than 180°. (Geometry Basics)
All regular polygons are always Convex polygons.
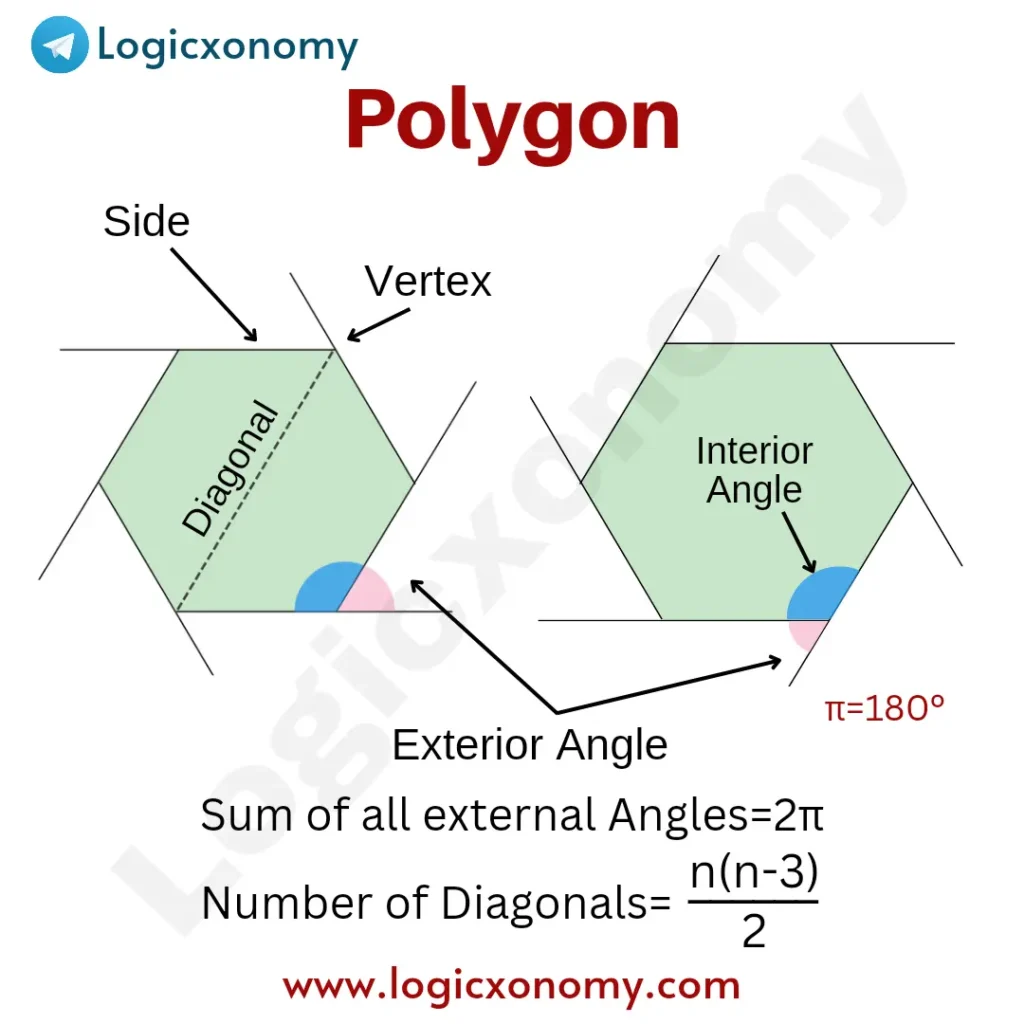
Important Formulas
(i) The Sum of all internal Angles of a Polygon= (n-2)𝛑
Here, n is the number of sides, and 𝛑=180° (Geometry Basics)
The Length of all sides of the Regular Polygon=a
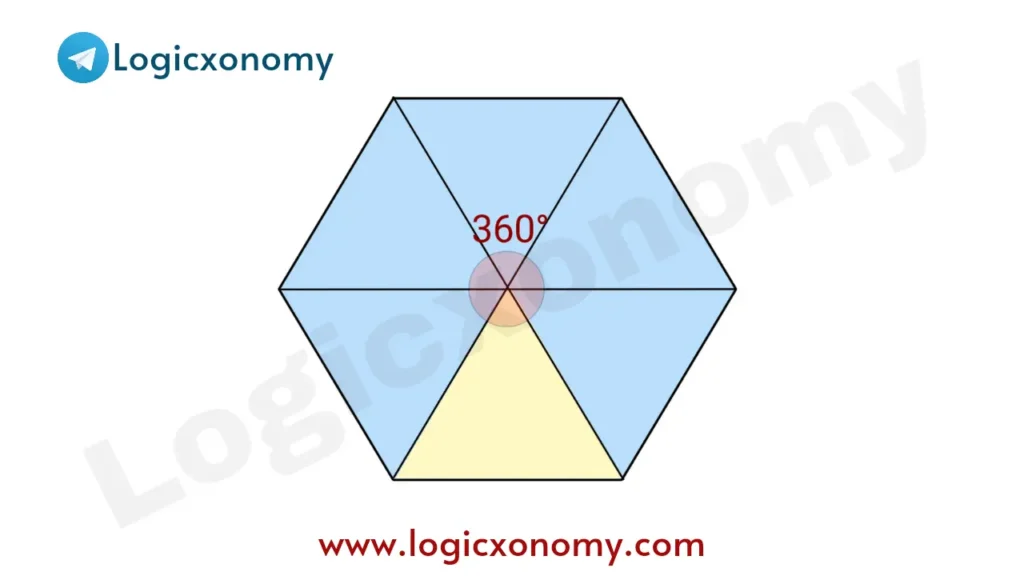
The sum of all Internal Angles of n triangles inside the given Polygon=n𝛑
Complete angle about center + Sum of all base angles=n𝛑
2𝛑 + Sum of all internal angles of the Polygon=n𝛑
The sum of all internal angles of the Polygon=(n-2)𝛑
In the case of a Regular Polygon (All angles Equal), each Internal Angle= \frac{(n-2)\pi}{n}
(ii) The Sum of all External Angles of a Polygon= 2𝛑 (Geometry Basics)
The sum of the pair of internal and external angle=𝛑 (Supplementary Angles)
The sum of all Internal angles + the Sum of all External Angles=n𝛑
(n-2)𝛑 + Sum of all External Angles=n𝛑
The sum of all External Angles=n𝛑 – (n-2)𝛑 = 2𝛑
(iii) Number of Diagonals of the Polygon =\frac{n(n-3)}{2}
Number of Diagonals = The number of ways by which any two vertices out of the given n vertices are selected – Number of the sides of the Polygon
Number of Diagonals =^nC_2-n
=\frac{n!}{2!(n-2)!}-n
=\frac{n(n-1)}{2}-n
=\frac{n^{2}-n-2n}{2}
=\frac{n(n-3)}{2}
(iv) Area of the Regular Polygon= \frac{na^{2}}{4} Cot (\frac{\pi}{n})
Area of the Regular Polygon (A)= Sum of the Areas of all Congruent Triangles
A= n\times \frac{1}{2}\times Base\times Height =\frac{n}{2}\times ah ……….(i)
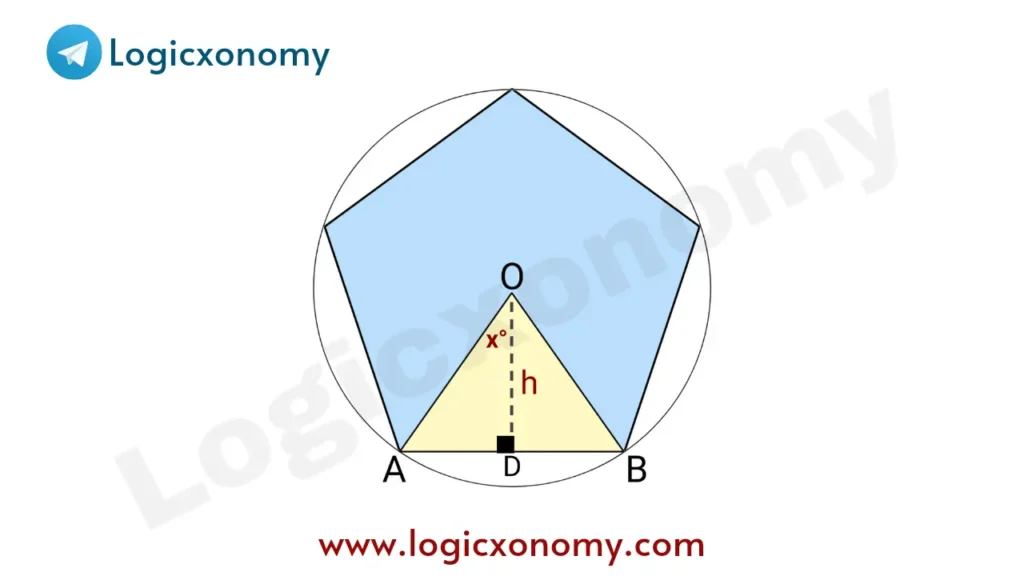
In △AOB, ∠AOB= \frac{2\pi}{n}
∠AOD (x) = \frac{\pi}{n}
AD=\frac{a}{2}
tan(x)=\frac{AD}{OD}=\frac{\frac{a}{2}}{h}
h=\frac{a}{2}Cot(\frac{\pi}{n}) …………(ii)
Area of the Polygon A=\frac{n}{2}\times ah=\frac{na^{2}}{4} Cot (\frac{\pi}{n})
List of Polygons
| Number of Sides | Name of Polygon | No. of Sides | Name |
| 3 | Triangle | 16 | Hexadecagon |
| 4 | Quadrilateral | 17 | Heptadecagon |
| 5 | Pentagon | 18 | Octadecagon |
| 6 | Hexagon | 19 | Enneadecagon |
| 7 | Heptagon | 20 | Icosagon |
| 8 | Octagon | 30 | Triacontagon |
| 9 | Nonagon | 40 | Tetracontagon |
| 10 | Decagon | 50 | Pentacontagon |
| 11 | Hendecagon | 100 | Hectogon |
| 12 | Dodecagon | 1000 | Chiliagon |
| 13 | Tridecagon | 10,000 | Myriagon |
| 14 | Tetradecagon | 1,000,000 | Megagon |
| 15 | Pentadecagon | \infty | Apeirogon |
Quadrilaterals
A closed two-dimensional shape formed by four lines is called a Quadrilateral. Here we would learn some features of widely used quadrilaterals.
Square
A quadrilateral of equal side lengths. All internal angles of the square are equal (90°).
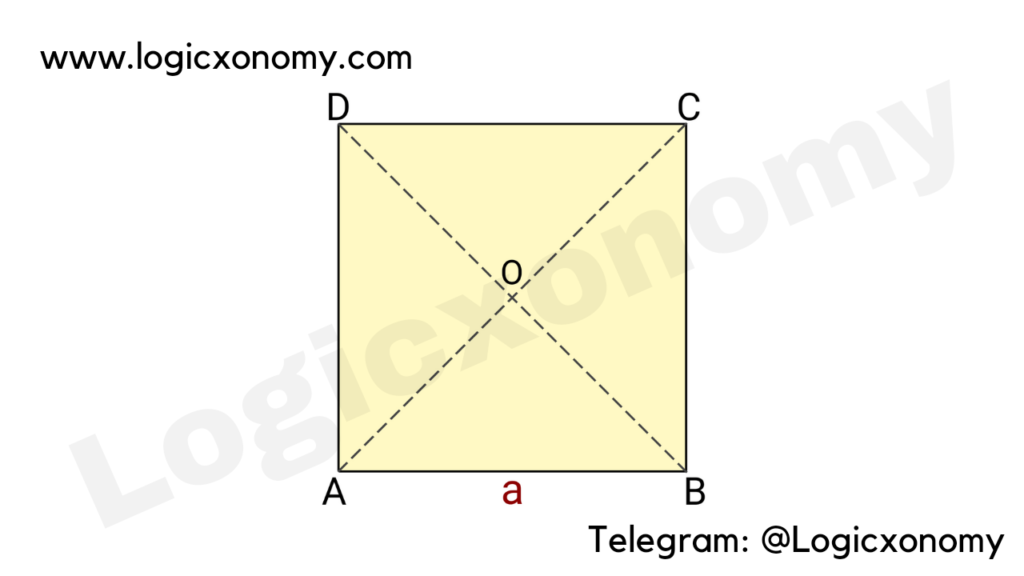
Let, the length of the side = a
AB ∥ DC and BC ∥ AD (Parallel)
Diagonals AC=BD=a\sqrt{2}
∠A=∠B=∠C=∠D=90°
AO=OC and BO=DO
AC ⟂ BD (Perpendicular)
Perimeter = The sum of all side lengths = 4a
Area=a^{2}
Rectangle
In a rectangle, all interior angles are 90 degrees but only opposite sides are equal in length.
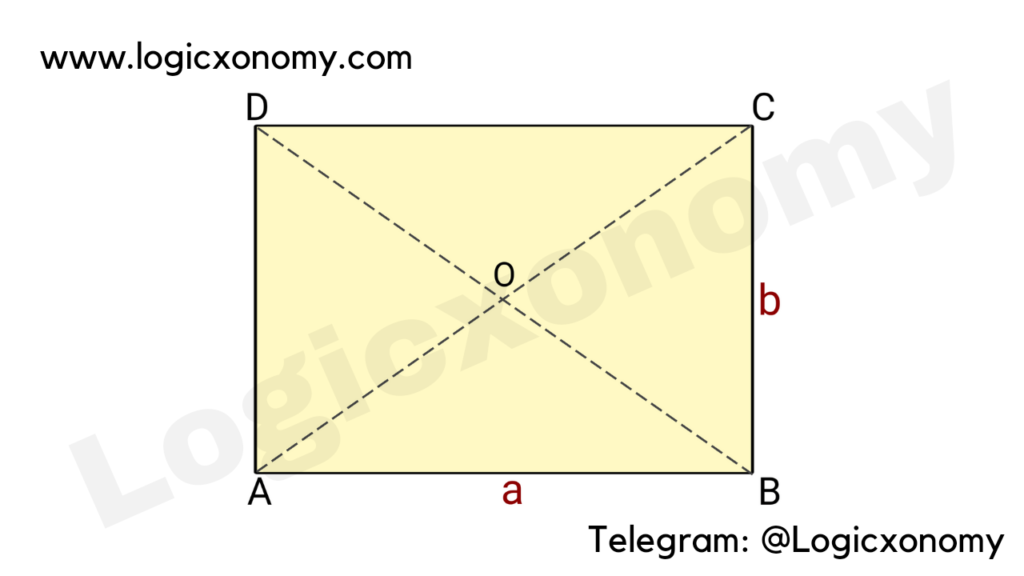
Let, length (AB)=a and Width (BC)=b
AB ∥ DC and BC ∥ AD (Parallel)
AB=DC and BC=AD
Diagonals AC=BD=\sqrt{a^{2}+b^{2}}
∠A=∠B=∠C=∠D=90°
AO=OC and BO=DO
Diagonal AC is not perpendicular to BD.
Perimeter = The sum of all side lengths = 2(a+b)
Area=length×Width= ab
Parallelogram
The opposite sides of the parallelogram are parallel to each other and equal.
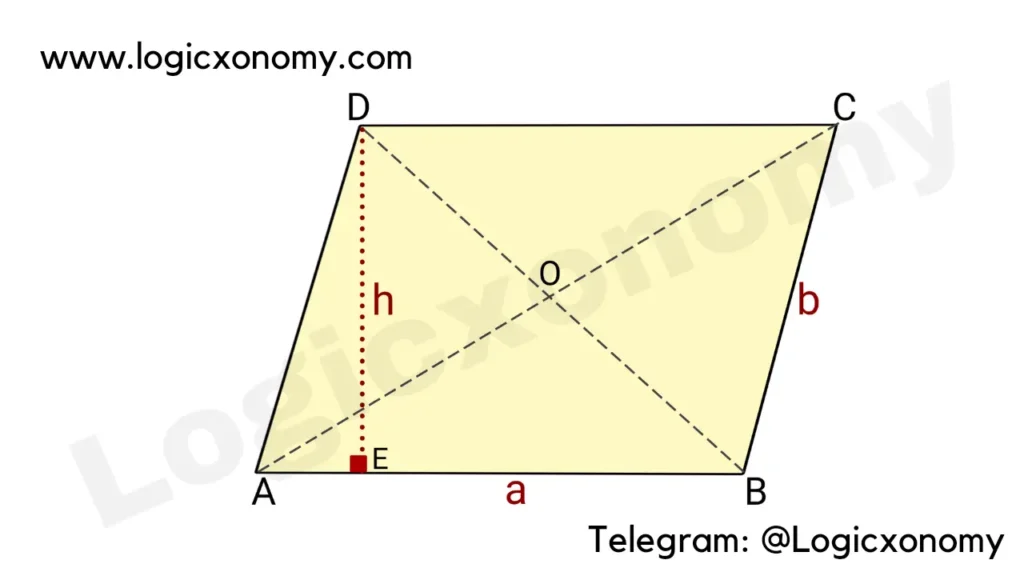
AB ∥ DC and AB=DC=a
BC ∥ AD and BC=AD=b
AC ≠ BD
AO=OC and BO=OD
Diagonal AC is not perpendicular to BD.
∠A=∠C and ∠B=∠D
Two angles on the same side are supplementary (∠A+∠B=180° and ∠B+∠C= 180°)
Perimeter = The sum of all side lengths = 2(a+b)
Area=length×Height= ah
Area=AB×AD×Sin(A)
Rhombus
A special type of parallelogram, whose all sides are equal in length.
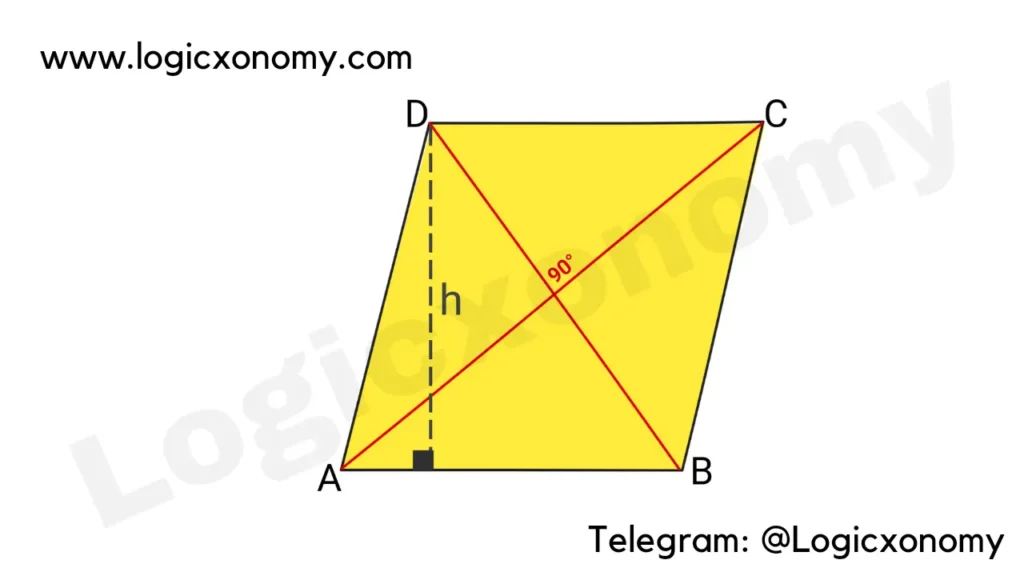
AB=BC=CD=DA=a
AB ∥ DC and BC ∥ AD (Parallel)
AC ≠ BD (Geometry Basics)
AO=OC and BO=OD (O, the intersection point of diagonals)
∠A=∠C and ∠B=∠D
AC ⟂ BD (Perpendicular)
Perimeter = The sum of all side lengths = 4a
Area=length×Height= ah
Area=AB×AD×Sin(A)= a^{2}\times Sin(A)
Area=\frac{1}{2}\times AC\times BD
Trapezium or Trapezoid
In a trapezium, only one pair of opposite sides are parallel and parallel lines can’t be equal in length.
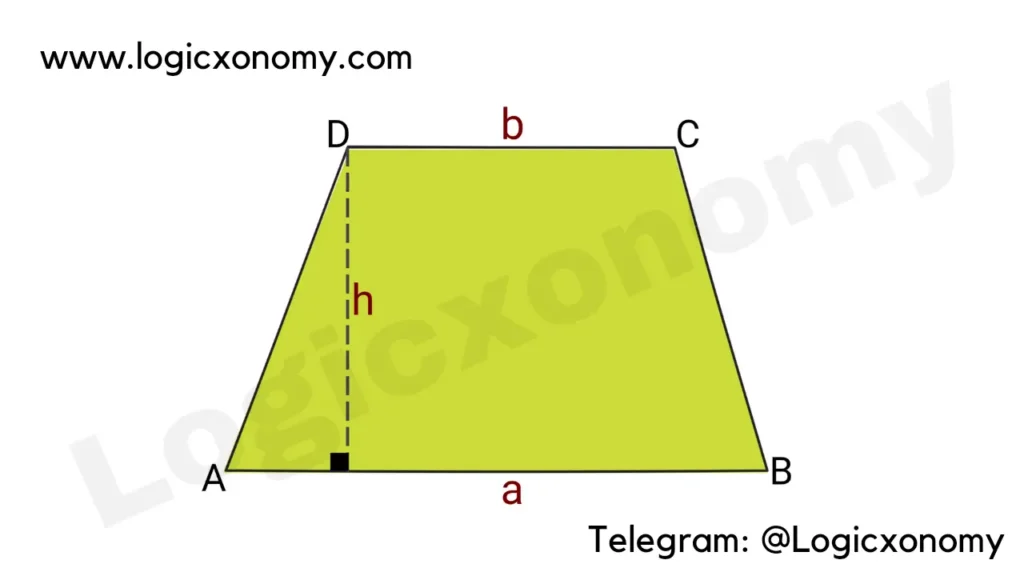
AB ∥ DC (Parallel)
If AD=BC then ABCD is called an Isosceles trapezium (Geometry Basics)
Area= \frac{1}{2}\times (a+b)\times h
Kite
It has two pairs of equal sides and two equal sides share one common starting point.
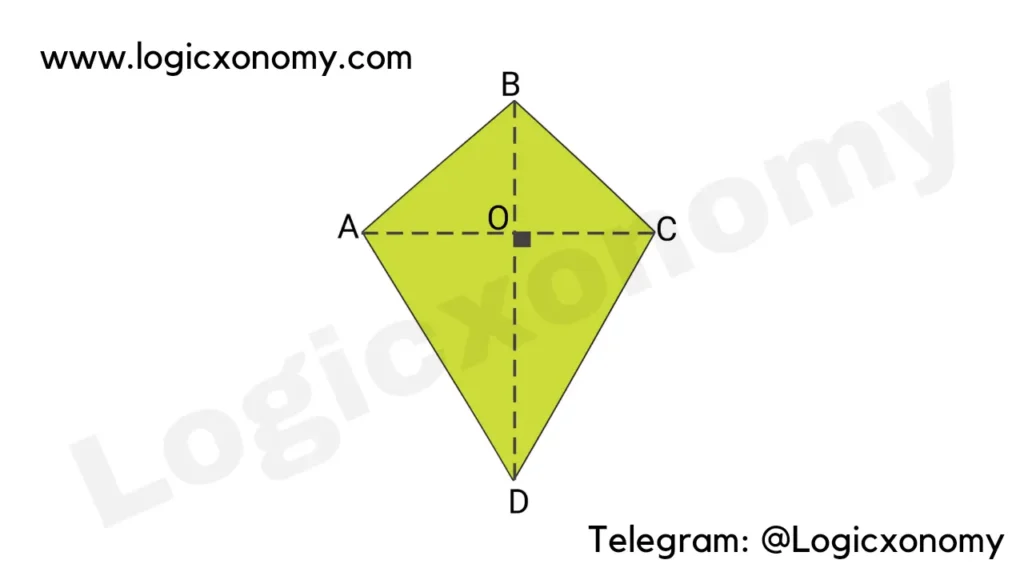
AB=BC and AD=DC (Geometry Basics)
AC ⟂ BD (Perpendicular)
Area= \frac{1}{2}\times AC\times BD
Cyclic Quadrilateral
A quadrilateral whose all vertices lie on the circumference of a circle is called a Cyclic quadrilateral.
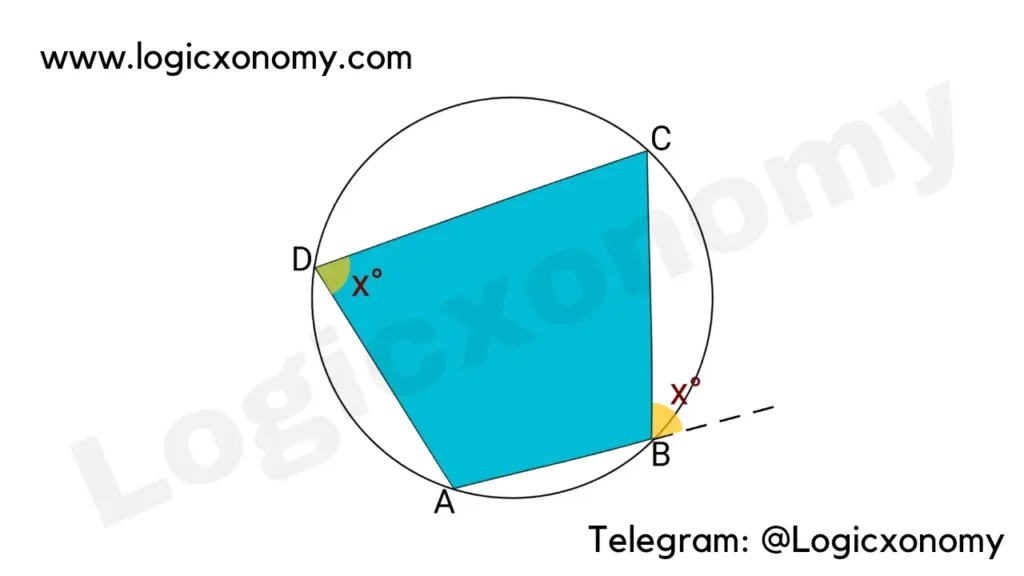
The Opposite angles are Supplementary angles. (Geometry Basics)
∠A+∠C=180° and ∠B+∠D=180°
The exterior angle of a cyclic quadrilateral is always equal to the interior angle of the opposite vertex.
Cyclic Quadrilateral in Detail (All theorems with Proof): Click Here
Circle
A two-dimensional curved shape whose all points are equidistant from a particular point (center) is called a ‘Circle’.
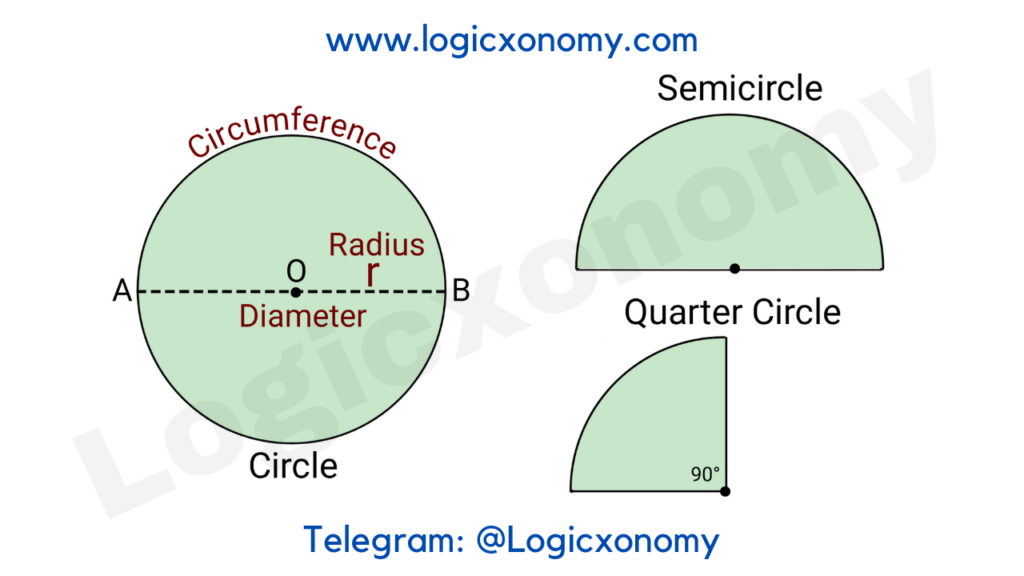
The radius of the Circle= r
Diameter (AB)= 2r
Circumference = 2\pi r
Area= \pi r^{2}
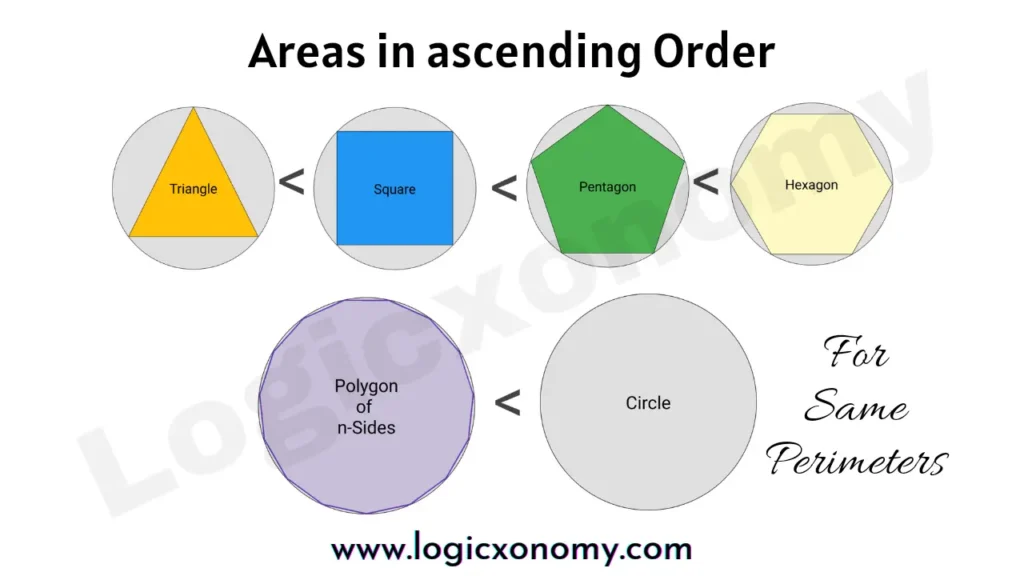
Comparison of Areas and Perimeters of the Geometric shapes
In the case of the same perimeter, the area of the circle is the largest in comparison to any polygon.
Example: For a circle and a square of the same perimeter
2𝜋r = 4a
Here, r is the length of the radius of the Circle and a is the length of the sides of the Square.
Area of the Sqaure= a^{2} =(\frac{\pi r}{2})^{2}=(\frac{\pi}{4})\times \pi r^{2}= 0.78 × Area of the Circle
Similarly, we can prove it for all polygons.
In the case of the same area of Geometric shapes, the perimeter of the circle is the smallest.
Example: For a circle and a square of the same area (Geometry Basics)
\pi r^{2} = a^{2}
Perimeter of the Circle= 2\pi r= 2\pi ×\frac{a}{\sqrt{\pi}} =2a\sqrt{\pi}
=4a\times \frac{\sqrt{\pi}}{2}
=0.88× The Perimeter of the Square
Similarly, we can prove it for all polygons.
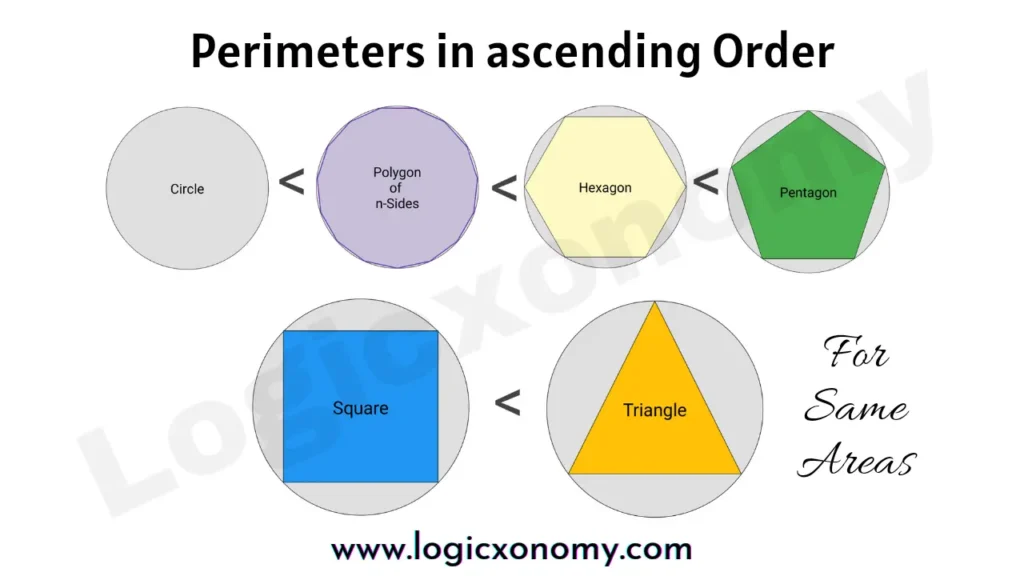
Note: If the number of the sides of Polygons is the same. (Geometry Basics)
Case 1: For equal areas of Polygons, the perimeter of the Regular Polygon is the smallest.
Case 2: For equal perimeters of Polygons, the area of the Regular Polygon is the largest.
Solid Geometry (3D)
Here we would learn about the characteristics and formulas of three-dimensional shapes. (Geometry Basics)
Cube
A solid or hollow three-dimensional shape that has 8 vertices and 6 square faces. So, the length, width, and height of a Cube are always equal.
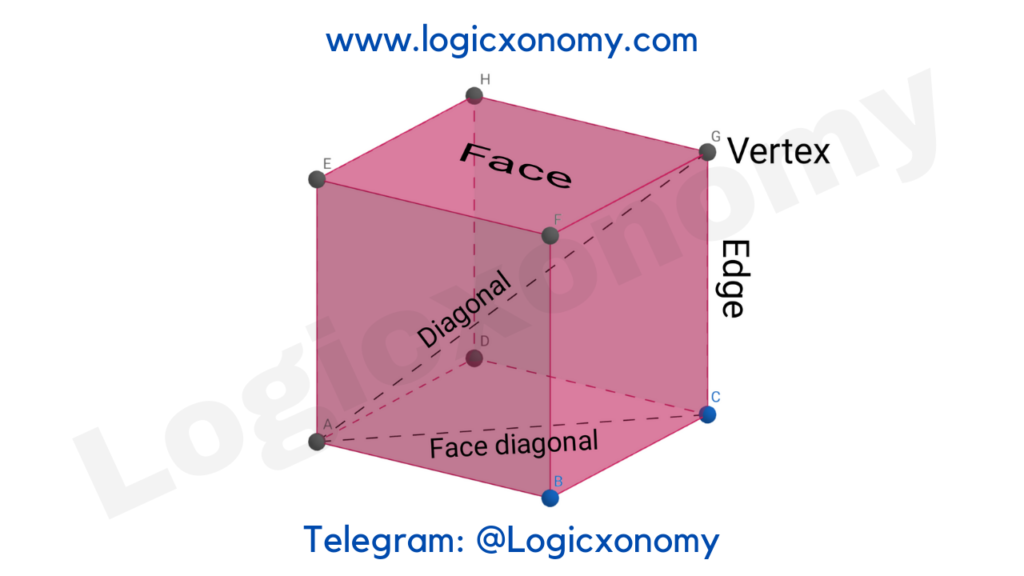
Let, the length of the Cube=a
Lateral Surface Area= 4×Area of a square face = 4\times a^{2}
Total Surface Area= 6×Area of a square face = 6\times a^{2}
Volume= a^{3}
Number of Vertices = 8
Number of Edges= 12
Length of a face diagonal = a\sqrt{2}
Length of the diagonal of a Cube = a\sqrt{3}
Total Surface Area: The total area of all faces of a 3D shape. (Geometry Basics)
Lateral Surface Area: Total Surface Area – Area of the Top & Bottom faces.
Cuboid
A cube-like 3D shape, which has a different length, width, and height. (Geometry Basics)
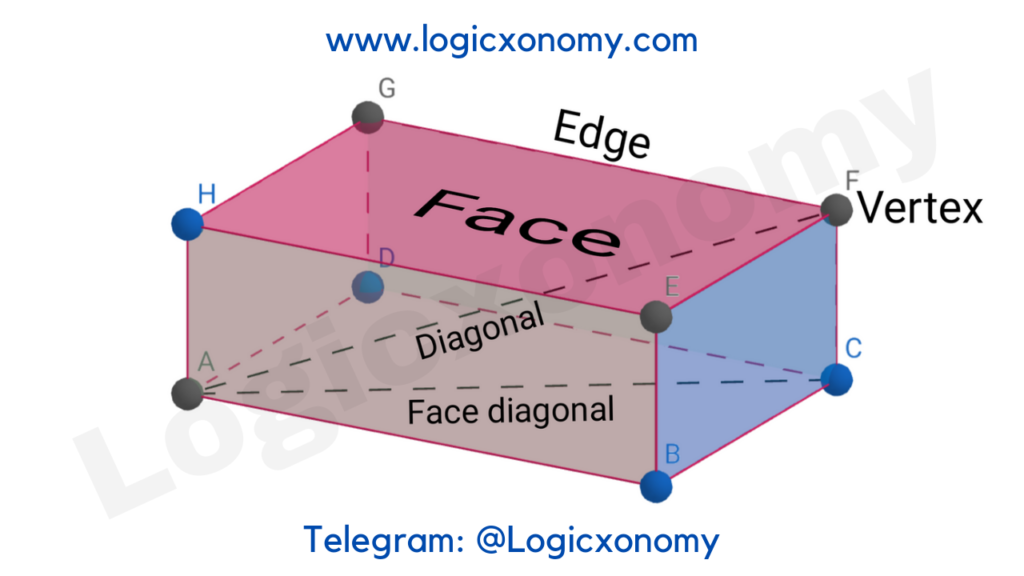
Let, the length, width, and height of a Cuboid are l, b, and h respectively.
AB=l
BC=b
BE=h
Total Surface Area= 2\times (lb+bh+hl)
Lateral Surface Area= 2\times (l+b)\times h
Length of the Diagonal= \sqrt{l^{2}+b^{2}+h^{2}}
Volume= Base Area×Height= l\times b\times h
Cylinder
A 3D shape in which two Circular and parallel bases are connected by a curved surface. (Geometry Basics)
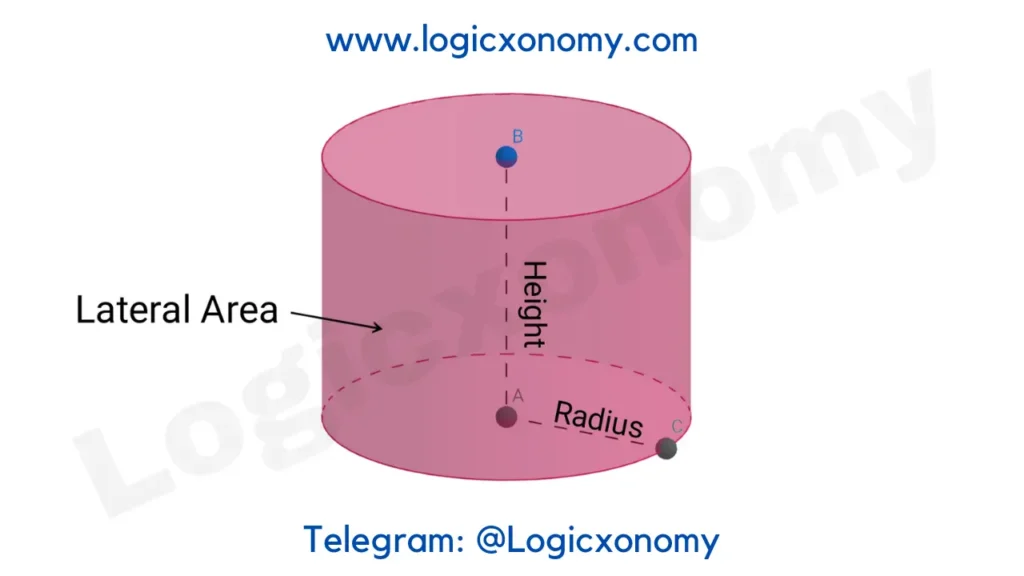
Let, the length of the radius of the circular base= r
Height= h
Lateral Surface Area= Area of Curved face = 2\pi rh
Total Surface Area= Curved Area + Top & Base Area
=2\pi rh+2\pi r^{2}
=2\pi r(h+r)
Volume= Base Area×Height = \pi r^{2}h
Cone
A 3D shape that narrows smoothly from a circular base to a pointed top (Apex).
Here we consider a Right Circular cone. In a right circular cone, the axis of the cone (line meeting the apex and center of the base) is perpendicular to the base.
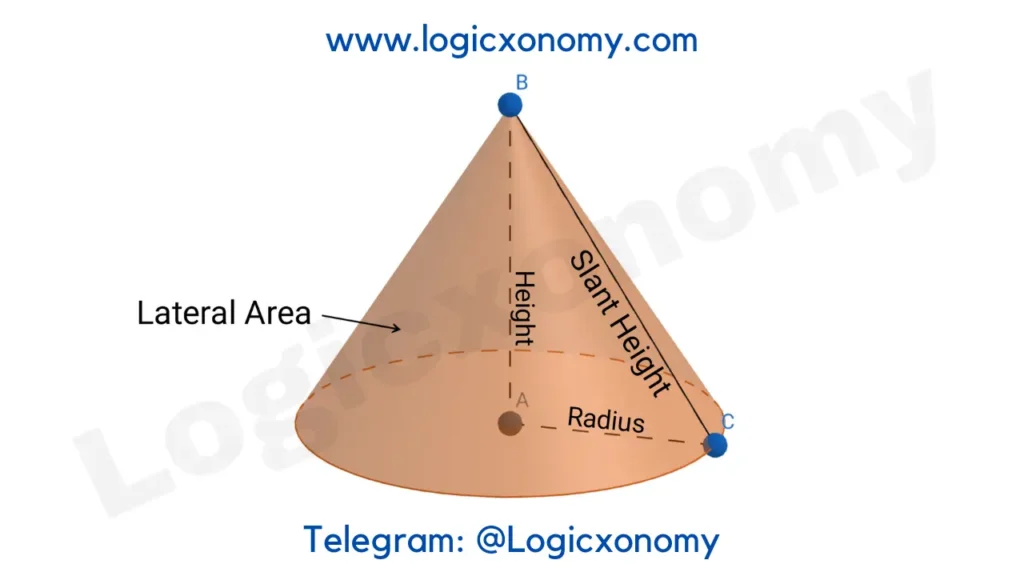
Let, the length of the radius of the circular base= r
Height= h
Slant height (l)= \sqrt{r^{2}+h^{2}}
Lateral Surface Area = \pi rl
Total Surface Area= \pi rl+\pi r^{2}= \pi r(l+r)
Volume = \frac{1}{3} ×Base Area×Height = \frac{1}{3}\pi r^{2}h
Sphere and Hemisphere
A 3D shape that has all its surface points equidistant from a common point (Center). The sphere is analogous to a Circle in 2D geometry. The Hemisphere is exactly half of the sphere.
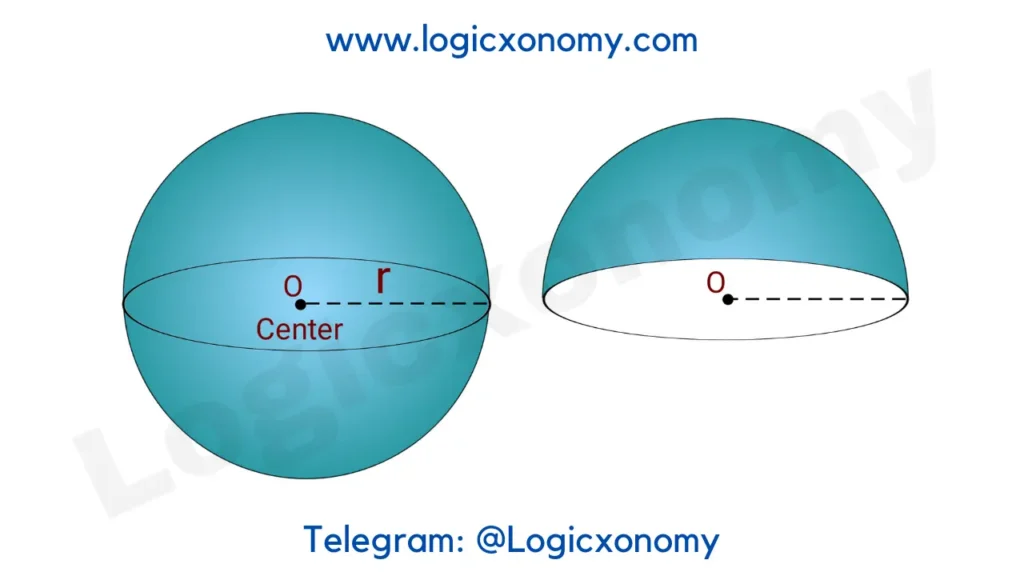
Let, the length of the radius= r
(i) Sphere (Geometry Basics)
Total Surface Area (Lateral Surface)= 4\pi r^{2}
Volume= \frac{4}{3}\pi r^{3}
(ii) Hemisphere (Geometry Basics)
Lateral Surface Area= 2\pi r^{2}
Total Surface Area= Lateral Area + Base area =2\pi r^{2}+\pi r^{2} =3\pi r^{2}
Prism
A solid shape that has two identical and parallel faces (Polygon).
If the axis of the prism (line meeting the centers of top and bottom faces) is perpendicular to the base, it’s called the ‘Right prism’ otherwise it’s an ‘Oblique prism’.
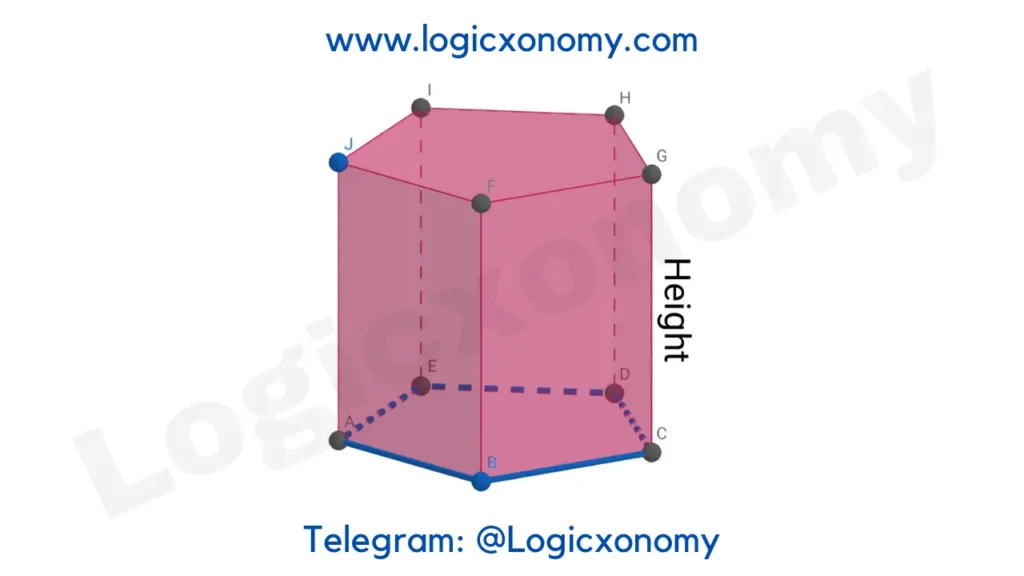
The volume of the Prism= Base Area×Height
Pyramid
A 3D shape, similar to the Cone with a Polygon base is called a Pyramid.
The volume of the Pyramid= \frac{1}{3}×Base Area×Height
A Pyramid whose all faces are an Equilateral triangle is called a Regular Tetrahedron.
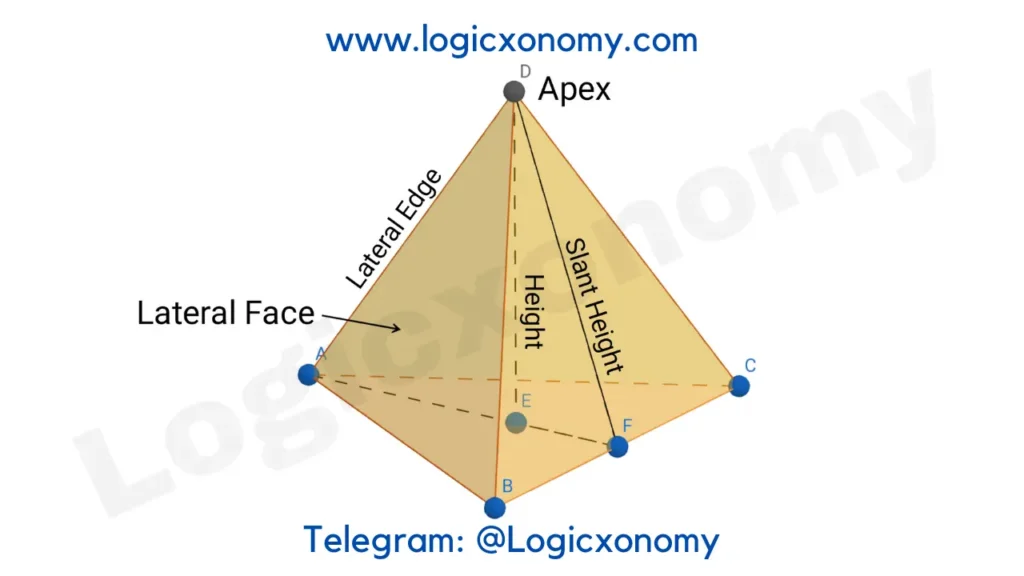
The number of faces= 4
Number of Edges=6
Number of vertices=4
Let, the length of each edge=a
Height = \sqrt{\frac{2}{3}}\times a
Slant Height= \frac{\sqrt{3}}{2}\times a
Volume= \frac{a^{3}}{6\sqrt{2}}
Polyhedron
A 3D solid that has a finite number of Polygon faces. Example: Prism, Pyramid, Cube, etc.
Let, F is the number of faces
V is the number of vertices
E is the number of edges
Then, F+V=E+2 (Euler’s Formula)
Oblique Cylinder and Cone
If the axis of the Cylinder or Cone is not perpendicular to the base, it’s an Oblique Cylinder or an Oblique Cone respectively.
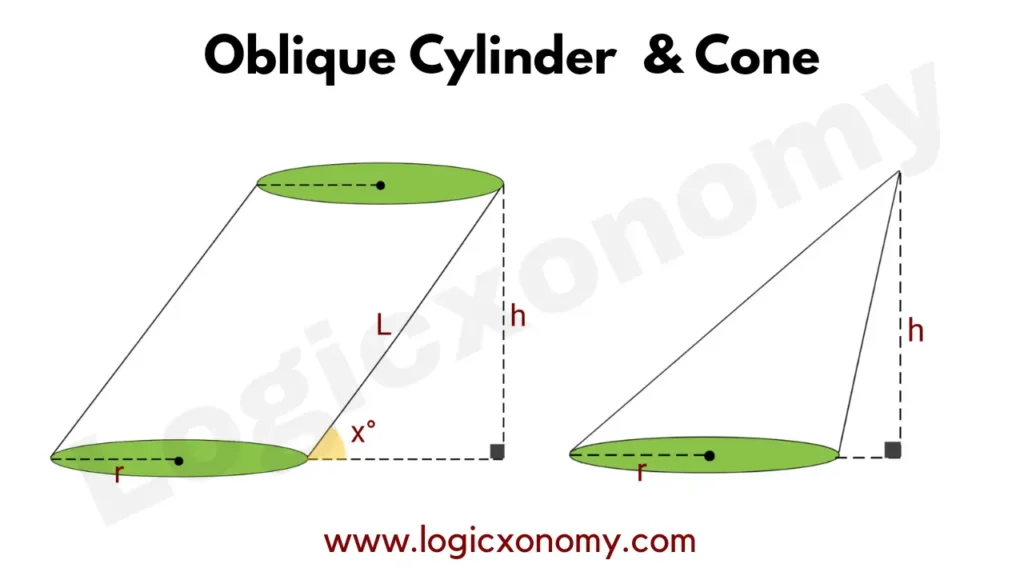
Heights of both the shapes =h
The length of the radius of the Circular base= r
The volume of the Oblique Cylinder= \pi r^{2}h
Volume of the Oblique Cone= \frac{1}{3}\pi r^{2}h
Frustum of a Cone
If a Cone is cut by a plane parallel to its base, the lower part is called its Frustum. (Geometry Basics)
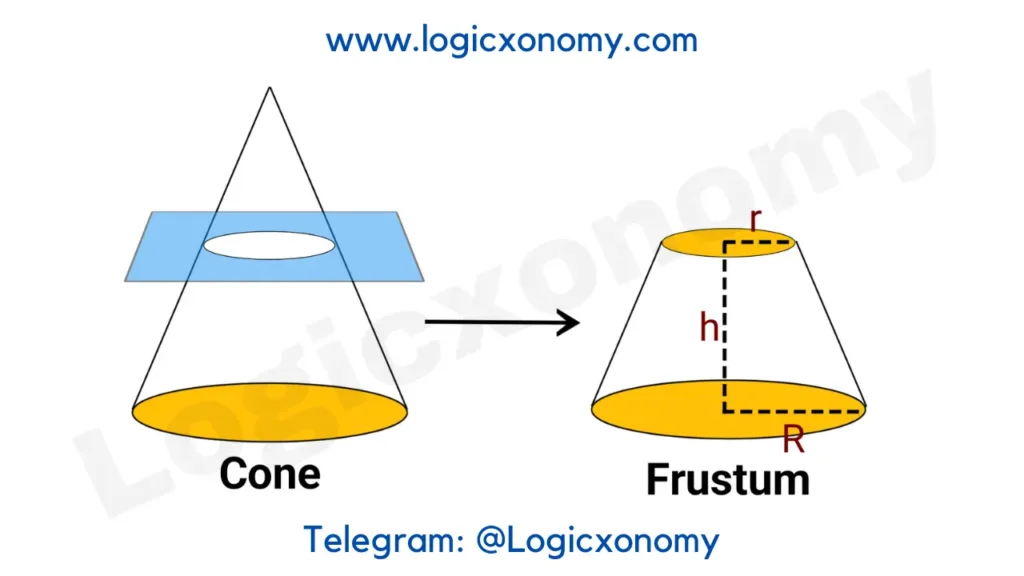
Slant Height of the Frustum (L)= \sqrt{h^{2}+(R-r)^{2}}
Lateral Surface Area= \pi (r+R)L
Total Surface Area= \pi (r+R)L +\pi (r^{2}+R^{2})
Volume= \frac{1}{3}\pi (r^{2}+rR+R^{2})\times h
Trapezoidal Prism
A 3D shape, having two parallel Trapezoidal faces connected by four rectangles. (Geometry Basics)
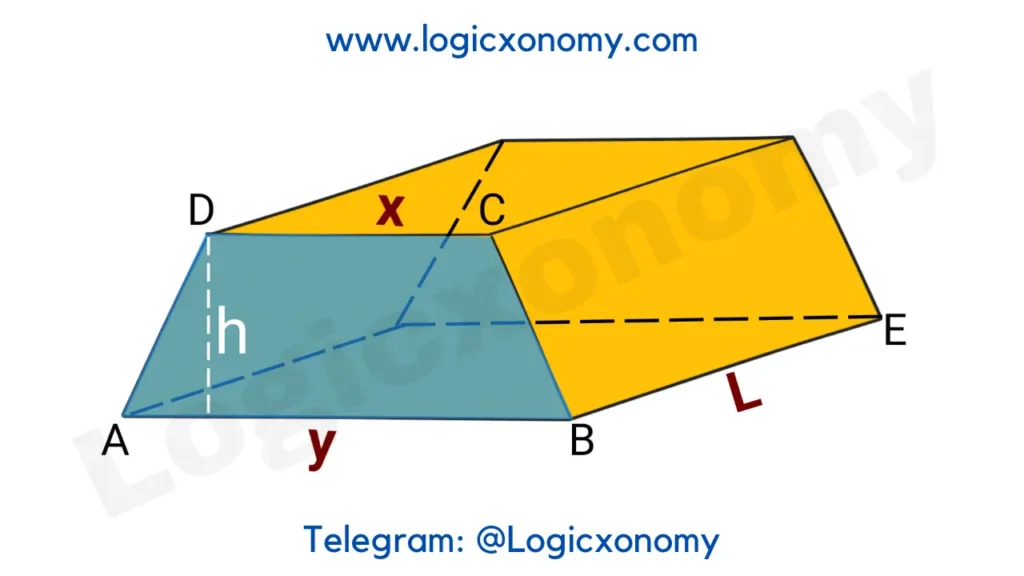
Volume = Area of Trapezoid ABCD × BE
= \frac{1}{2}(x+y)\times h\times L
More Concepts are coming soon…

