Surds and indices chapter plays a crucial role in simplification problems of arithmetic. Here we would learn about its basic concepts and tricks to handle these problems efficiently in competitive examinations.
Surds: A surd is a root of a rational number with an irrational value. In other words, when it is a root and irrational, it is surd. Surds can not be further simplified into whole numbers or integers.
Example: \sqrt{2}, \sqrt{3}, \sqrt[3]{5}, \sqrt{\frac{1}{7}}, etc.
Note: An irrational number is a real number that can not be written as a simple fraction.
Example: \pi, \sqrt{2},\sqrt{3}, etc.
If N is an irrational number then N\neq\frac{p}{q}, where p and q are integers and q\neq0.
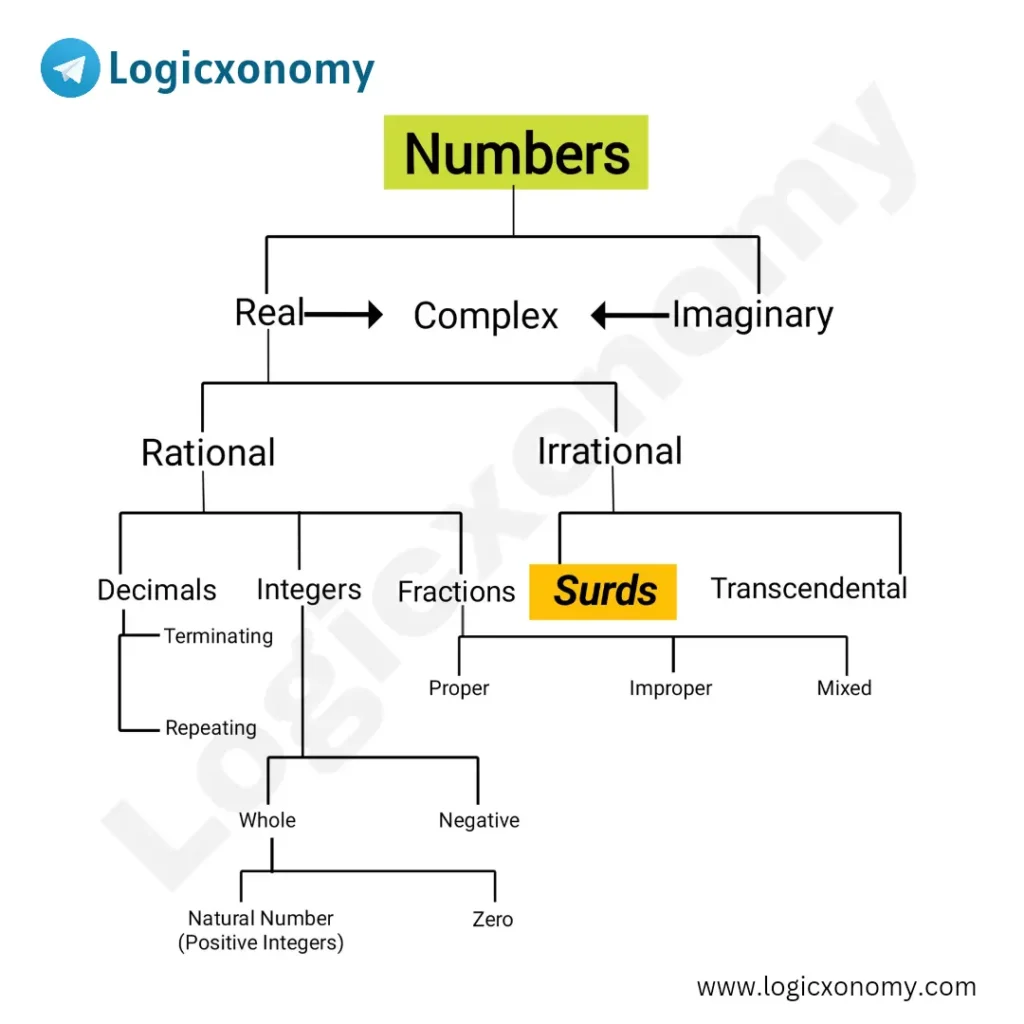
Types of Surds
- Pure Surds: When surds have only one irrational number.
Example: \sqrt{2}, \sqrt{11}, \sqrt{17}, etc.
- Mixed Surds: When surds have both rational and irrational numbers.
Example: 2\sqrt{5}, 4\sqrt{7}, 8\sqrt{3}, etc.
- Compound Surds: When there are two or more surds in one mathematical expression.
Example: 4+\sqrt{5}, \sqrt{5}+\sqrt{6}, 3+2\sqrt{6}, etc.
Indices: The index (Plural: Indices) is the power (exponent) of a number.
Example: 2^{5} has an index of 5 and 2 is its base. Here exponent 5 defines, how many times 2 has been multiplied by itself.
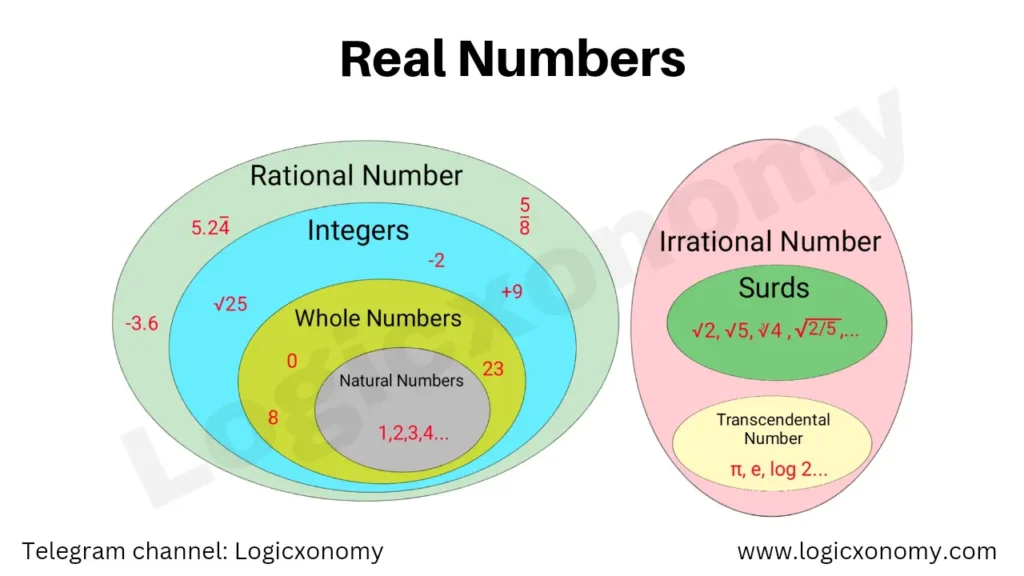
Difference Between Rational and Irrational Numbers
| Rational Number | Irrational Number |
| Rational Numbers can be expressed in the form of \frac{p}{q}, where p and q are integers and q\neq0. | Irrational Numbers can’t be expressed in \frac{p}{q} form. |
| Rational Numbers include finite and recurring decimals. | Irrational Numbers consist of non-recurring and non-terminating decimals. |
| Square roots of perfect squares and cube roots of perfect cubes are rational. | It includes surds. |
| Examples: -3 ,0 ,1 ,\frac{5}{8}, \sqrt{25}, \sqrt{\frac{1}{9}}, etc. | Examples: \pi, e ,\sqrt{7} ,\sqrt{\frac{2}{5}} ,etc. |
Rules of Surds and Indices
If a and b are any two real numbers, m and n are integers then
(i) a^{m}\times a^{n}=a^{m+n}
Example: 2^{3}\times 2^{5}=2^{8}=256
(ii) \frac{a^{m}}{a^{n}}=a^{m-n}
Example: \frac{5^{3}}{5^{4}}=5^{-1}=\frac{1}{5}
(iii) (ab)^{m}=a^{m}\times b^{m}
(iv) x^{m^{n}}=x^{(m^{n})}
(v) (a^{m})^{n}=a^{m\times n}
(vi) a^{-m}=\frac{1}{a^{m}}
(vii) a^{0}=1
(viii) \sqrt[n]{a}=a^{\frac{1}{n}}
(ix) \sqrt[n]{x^m}=x^{\frac{m}{n}}
(x) If x^{\frac{1}{n}}=a then x=a^{n}
(xi) \sqrt{a}\displaystyle\pm \sqrt{b} \neq \sqrt{a\displaystyle\pm b}
(xii) \sqrt{a}\times \sqrt{b}=\sqrt{ab}
(xiii) \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}
Rationalizing Surds
Rationalization is the process of changing the denominator of a fraction to a rational number.
Que: Rationalize \frac{1}{\sqrt{5}+\sqrt{3}}.
Solution: Multiply the conjugate of the denominator by both, the numerator and the denominator.
=\frac{1\times (\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})\times (\sqrt{5}-\sqrt{3})}
=\frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}
=\frac{1}{2}\times (\sqrt{5}-\sqrt{3})
Surds and Indices problems
Que 1: Find the value of \frac{(243)^\frac{n}{5}\times 3^{2n+1}}{9^{n}\times 3^{n-1}}.
Solution: Numerator =(3^{5})^{\frac{n}{5}}\times 3^{2n+1}=3^{n}\times 3^{2n+1}=3^{3n+1}
Denominator=3^{2n}\times 3^{n-1}=3^{3n-1}
\frac{3^{3n+1}}{3^{3n-1}}=3^{(3n+1)-(3n-1)}=3^{2}=9Que 2: If x^{x\sqrt{x}}=(x\sqrt{x})^{x} then find the value of x?
Solution: x^{x^{1}\times x^{\frac{1}{2}}}=(x^{1}\times x^{\frac{1}{2}})^{x}.
x^{x^{\frac{3}{2}}}=(x^{\frac{3}{2}})^{x}.
So, x^{\frac{3}{2}}=\frac{3x}{2}.
After squaring both sides of the equation,
x^{3}=\frac{9x^{2}}{4}.
x^{2}(x-\frac{9}{4})=0.
Now, x=\frac{9}{4} is the correct answer (x=0 would give an indeterminate value)
Que 3: Find the value of \frac{5^{n+3}-6\times 5^{n+1}}{9\times 5^{n}-5^{n}\times 2^{2}}?
Solution: \frac{5^{n}(5^{3}-6\times 5)}{5^{n}(9-4)}.
=\frac{125-30}{5}=19
Que 4: Find the value of [(\sqrt[3]{256^{2}})^{\frac{3}{2}}]^{\frac{1}{4}}?
Solution: 256=2^{8}
=[(2^{\frac{8\times 2}{3}})^{\frac{3}{2}}]^{\frac{1}{4}}
=(2^{8})^{\frac{1}{4}}=2^{2}=4

Que 5: Find the value of \sqrt[3]{4\frac{12}{125}}?
Solution: 4\frac{12}{125}=\frac{512}{125}=(\frac{8}{5})^{3}
So, The correct answer=\frac{8}{5}=1\frac{3}{5}
Que 6: If \frac{\sqrt{4356\times \sqrt{x}}}{\sqrt{6084}}=11, then find the value of x ?
Solution: After squaring both sides of the equation,
\frac{4356\times\sqrt{x}}{6084}=121.
\sqrt{x}=169.
x=169^{2}=28561.
Note: Click here for Quick Calculation Tips and Tricks.
Que 7: Arrange the following in ascending order if a>1
(i) \sqrt[3]{\sqrt[4]{a^{3}}}
(ii) \sqrt[3]{\sqrt[5]{a^{2}}}
(iii) \sqrt{\sqrt[3]{a}}
(iv) \sqrt{\sqrt[5]{a^{3}}}
Solution: \sqrt[3]{\sqrt[4]{a^{3}}}=(\sqrt[4]{a^{3}})^{\frac{1}{3}}=(a^{\frac{3}{4}})^{\frac{1}{3}}=a^{\frac{1}{4}}.
\sqrt[3]{\sqrt[5]{a^{4}}}=(\sqrt[5]{a^{4}})^{\frac{1}{3}}=(a^{\frac{4}{5}})^{\frac{1}{3}}=a^{\frac{4}{15}}.
\sqrt{\sqrt[3]{a}}=(a^{\frac{1}{3}})^{\frac{1}{2}}=a^{\frac{1}{6}}.
\sqrt{\sqrt[5]{a^{3}}}=(\sqrt[5]{a^{3}})^{\frac{1}{2}}=(a^{\frac{3}{5}})^{\frac{1}{2}}=a^{\frac{3}{10}}.
Now compare exponents,
(\frac{1}{4}, \frac{4}{15}, \frac{1}{6}, \frac{3}{10})\times 60=(15, 16, 10, 18).
Here, LCM(4,15,6,10)=60
Now, 10<15<16<18
So, \frac{1}{6}< \frac{1}{4}<\frac{4}{15}<\frac{3}{10}
Correct ascending order= (iii)<(i)<(ii)<(iv)
Que 8: Find the square root of \sqrt{5+2\sqrt{6}} ?
Solution: \sqrt{(\sqrt{3})^{2}+(\sqrt{2})^{2}+2\times\sqrt{3}\times\sqrt{2}}.
=\sqrt{(\sqrt{3}+\sqrt{2})^{2}}
=\sqrt{3}+\sqrt{2}
Important results of Surds and Indices
1. If N=\sqrt{x+\sqrt{x+\sqrt{x+\sqrt{x+......}}}}
Then N=\frac{1+\sqrt{1+4x}}{2}
Proof: N=\sqrt{x+N}.
N^{2}=x+N.
N^{2}-N-x=0.
N=\frac{1\displaystyle\pm\sqrt{1+4x}}{2}. (Sridharacharya Formula)
Note: N has a positive value so take the positive sign here.
2. If N=\sqrt{x-\sqrt{x-\sqrt{x-\sqrt{x-......}}}}
Then N=\frac{-1+\sqrt{1+4x}}{2}
3. If N=\sqrt{x\displaystyle\pm\sqrt{x\displaystyle\pm\sqrt{x\displaystyle\pm\sqrt{x\displaystyle\pm......}}}} then find the value of N?
Here x=k×(k+1), k is a Natural Number (Positive Integer)
Case 1: (+) sign
N=k+1
Case 2: (-) sign
N=k
Example: N=\sqrt{12+\sqrt{12+\sqrt{12+\sqrt{12+......}}}}=4
N=\sqrt{12-\sqrt{12-\sqrt{12-\sqrt{12-......}}}}=3
Here, 12=3×4
4. If N=\sqrt{x\sqrt{x\sqrt{x\sqrt{x......}}}} then N=x
Proof: N=\sqrt{x.N}.
N^{2}=x.N.
N(N-x)=0.
So, N=x (For x>0, N can’t be 0)
5. If K=\sqrt{x\sqrt{x\sqrt{x\sqrt{x.....n_{th}term}}}} then find the value of K ?
Number of terms= Number of square roots=n
K=(x)^{\frac{2^{n}-1}{2^{n}}}.
Example: K=\sqrt{5\sqrt{5\sqrt{5\sqrt{5}}}}=(5)^{\frac{2^{4}-1}{2^{4}}}=(5)^{\frac{15}{16}}.
Question: \frac{\sqrt{100!\sqrt{100!\sqrt{100!\sqrt{100!}}}}}{\sqrt{99!\sqrt{99!\sqrt{99!\sqrt{99!}}}}}=\sqrt[16]{10^x}
Find the value of x?
Solution: Numerator=(100!)^\frac{15}{16}.
Denominator=(99!)^\frac{15}{16}.
\sqrt[16]{10^x}=(100!/99!)^{\frac{15}{16}}=(100)^{\frac{15}{16}}=\sqrt[16]{10^{30}}The value of x=30
Frequently Asked Questions
What is the difference between Surds and Indices?
Surds can be expressed as the nth root of a rational number while Indices refer to the power to which a number is raised.
Is surd an irrational number?
Yes, Surd is irrational because, in decimal form, it goes on without repetition.
How can we identify Surds?
A rational number that contains a radical sign (\sqrt[n]{}) and its solution is an irrational value, called Surd.
Can a Surd be expressed in Index form?
Yes, A surd can be expressed in the form of a fractional index.
Surd Form: \sqrt[n]{a}
Index Form: a^{\frac{1}{n}}The square root of ‘pi’ is a Surd or not?
No, \pi is an irrational number but a Surd is the nth root of a rational number.
Classification of Numbers: Click Here
Multiple Choice Questions (MCQ)
35 Questions with solutions, based on the concepts of Surds and Indices.





