Concepts of Inradius and Circumradius of a triangle (Right angle). Here is the formula for the length of the Inradius and Circumradius of a Right angle triangle, with proof.
Inradius
The point of intersection of the angle bisectors of a triangle is called its Incenter. The distance of the incenter from all the sides of the triangle is equal. The altitude subtended from the incenter of a triangle to any of its sides is called the Inradius of the triangle. The incenter is the center of the inscribed circle (Incircle) of the triangle.
Let a △ABC in which BC=a, AC=b, and AB=c. The length of its semi-perimeter is ‘s’ and its area is represented by △.
Then, the length of its Inradius (r)=\frac{\triangle}{s}.
s=\frac{a+b+c}{2}.
Proof: In the given △ABC, I is the incentre of the triangle. From I draw perpendiculars to all the sides of the triangle. (Inradius and Circumradius of a triangle)
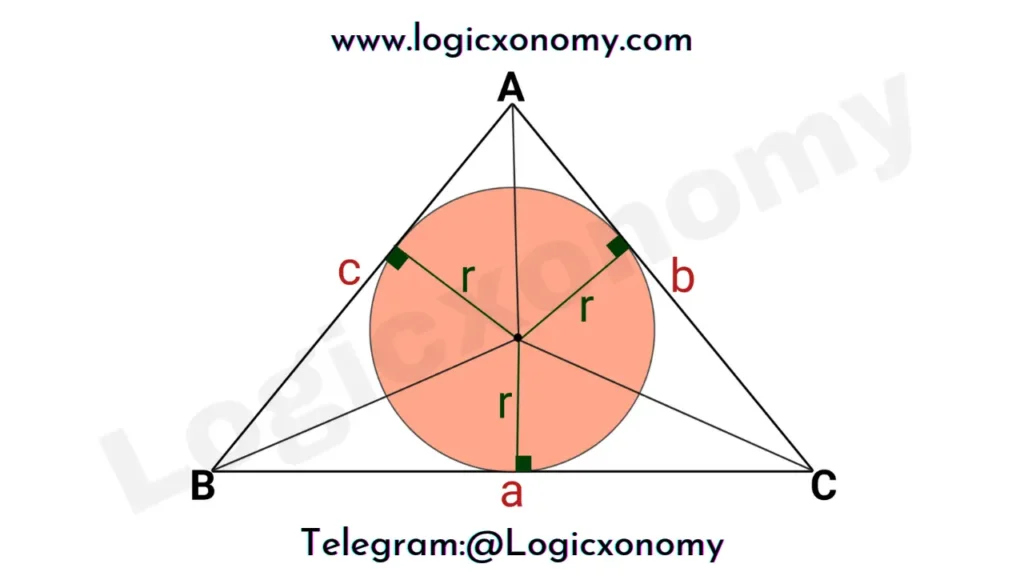
The area of the triangle= \frac{1}{2}\times Base\times Height.
ar(△ABC)= ar(△BIC)+ar(△CIA)+ar(△AIB)
△=\frac{1}{2}\times ar+\frac{1}{2}\times br+\frac{1}{2}\times cr
△=\frac{1}{2}\times r\times (a+b+c)
△=rs
Circumradius
The intersection point of the perpendicular bisectors of the sides of a triangle is called its Circumcenter. The distance of all the vertices of a triangle from its Circumcenter is equal and the line joining the circumcenter to any of the vertices is called its Circumradius. The circumcenter is the center of the circumscribed circle (Circumcircle) of the triangle.
The length of Circumradius (R)=\frac{abc}{4\triangle}.
Proof: Draw AE⟂BC and diameter AD of △ABC. Here O is the center of the circle & Circumcenter of the △ABC. The length of the circumradius is R, (AD=2R). (Inradius and Circumradius of a triangle)

△ABD ~ ∆AEC (Similar Triangles)
∠BDA=∠ECA (Subtended by same chord AB on the Circumference)
∠ABD=∠AEC=90°
By Similarity, \frac{AB}{AE}=\frac{AD}{AC}
\frac{c}{AE}=\frac{2R}{b}
AE=\frac{bc}{2R}
The area of △ABC, △=\frac{1}{2}\times BC\times AE
△=\frac{1}{2}\times a\times \frac{bc}{2R}
△=\frac{abc}{4R}
Heron’s Formula
Let a △ABC in which BC=a, AC=b, and AB=c. The length of its semi-perimeter is ‘s’ and its area is represented by △.
The area of △ABC, △=\frac{1}{2}\times bc\times Sin(A)
=\frac{1}{2}bc\times \sqrt{1-Cos^{2}A}
=\frac{1}{2}bc\times \sqrt{1-(\frac{b^{2}+c^{2}-a^{2}}{2bc})^{2}}
=\frac{1}{2}bc\times \frac{1}{2bc}\times \sqrt{(2bc)^{2}-(b^{2}+c^{2}-a^{2})^{2}}
Note: (x+y)^{2}=x^{2}+y^{2}+2xy and x^{2}-y^{2}=(x+y)(x-y).
=\frac{1}{4}\times \sqrt{(2bc+b^{2}+c^{2}-a^{2})(2bc-b^{2}-c^{2}+a^{2})}
=\frac{1}{4}\times \sqrt{[(b+c)^{2}-a^{2}]\times [a^{2}-(b-c)^{2}}
=\frac{1}{4}\times \sqrt{(b+c+a)(b+c-a)(a+b-c)(a+c-b)}
=\frac{1}{4}\times \sqrt{(2s)(2s-2a)(2s-2c)(2s-2b)}
△=\sqrt{s\times (s-a)\times (s-b)\times (s-c)}
Second Method: Use the formula of the area of Cyclic Quadrilateral
Area= \sqrt{(s-a)(s-b)(s-c)(s-d)}
Here d=0
So, The area of triangle= \sqrt{s\times (s-a)\times (s-b)\times (s-c)}

Euler’s Theorem
It is used to find the distance between the incenter and circumcenter of a triangle. Let a triangle ABC in which I is the incenter and O is the circumcenter, the length of the inradius and circumradius are r and R respectively.
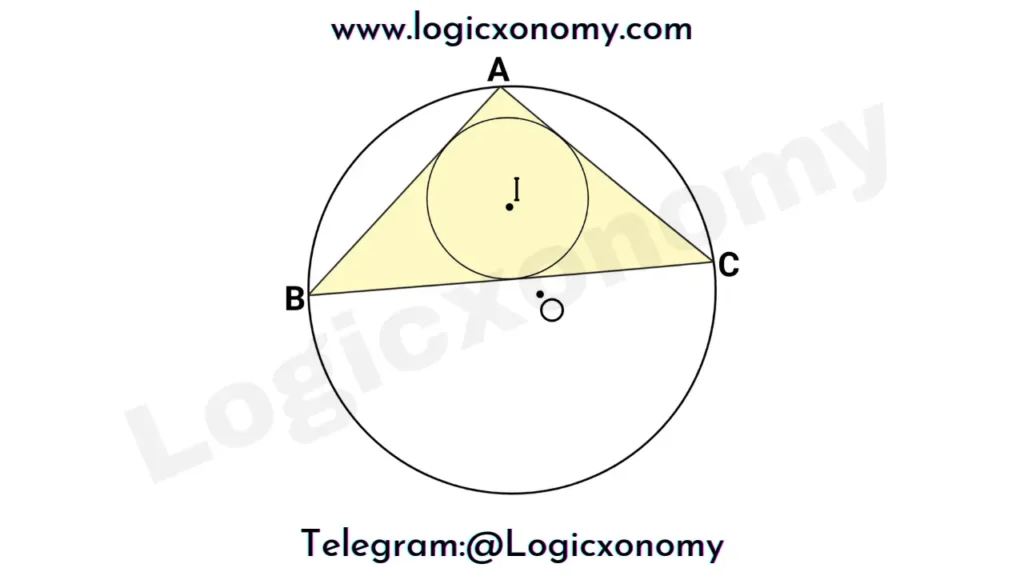
Draw lines AN, BI, and CI as given in the figure. (Inradius and Circumradius of a triangle)
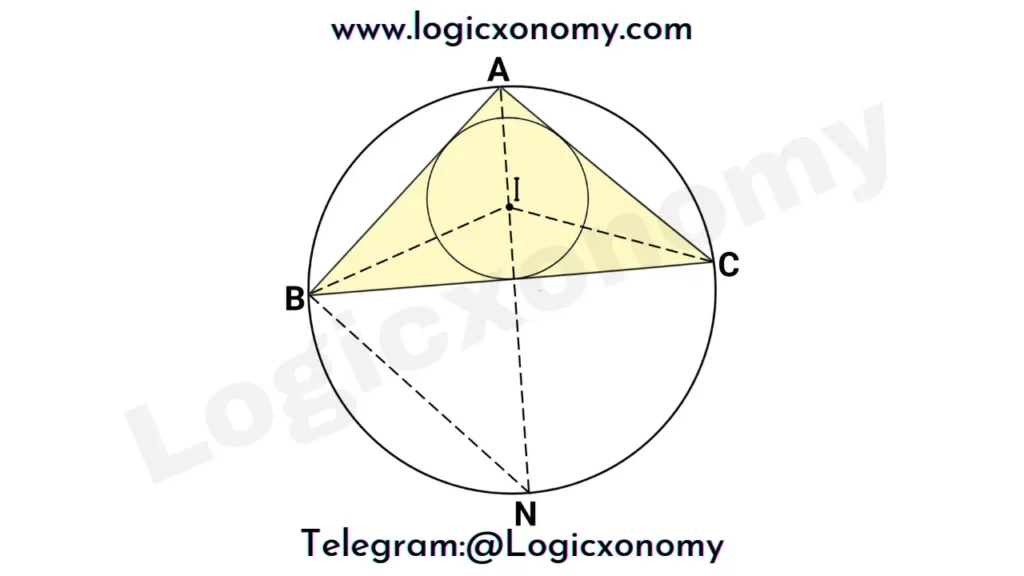
∠IAB= ∠IAC= A/2
∠ABI= ∠CBI= B/2 (I is the intersection point of angle bisectors)
∠NBC= ∠NAC= A/2 (Angles, subtended by the same chord NC)
∠BIN= ∠IBA+∠IAB= (A+B)/2 (External angle of the triangle)
In the △NBI, ∠NBI= ∠NIB
So, BN=IN …………(i)

Intersecting chord theorem, AI×IN=LI×IM
AI×IN=(R-d)×(R+d) …….(Circumradius=R)
AI×BN=R^{2}-d^{2} ………….(ii) (From equation i, BN=IN)

Draw ID⟂AB, so ID=r (Inradius)
NQ is the diameter so ∠NBQ=90° (Theorem)
Now, △NBQ ~ △IDA (Similar triangles)
\frac{ID}{BN}=\frac{AI}{QN}.
\frac{r}{BN}=\frac{AI}{2R}

AI×BN=2Rr
R^{2}-d^{2} =2Rr.
d=\sqrt{R\times (R-2r)}.
Euler’s Inequality
As we know the Arithmetic Mean (AM) is greater than or equal to Geometric Mean (GM) for non-negative numbers. (Inradius and Circumradius of a triangle)
AM≥GM
\frac{x+y}{2}\geq \sqrt{xy}.
x+y\geq 2\sqrt{xy}.
So, (x+y)(y+z)(z+x)\geq 8xyz.
Put x=s-a, y=s-b, and z=s-c
Here, s is the semi-perimeter of the triangle and 2s=a+b+c
(2s-a-b)(2s-b-c)(2s-a-c)\geq 8(s-a)(s-b)(s-c).
c\times a\times b\geq 8(s-a)(s-b)(s-c) ………(i)
R=\frac{abc}{4\triangle} (R, length of the Circumradius)
\triangle =\sqrt{s\times (s-a)(s-b)(s-c)} (Heron’s formula)
Put these two formulas in equation (i):
4R\triangle \geq 8\times \frac{\triangle^{2}}{s}
R\geq 2\times \frac{\triangle}{s}
R\geq 2r (Here, r is the length of the Inradius)
Note: The equality holds only for an Equilateral Triangle.
Inradius and Circumradius of a triangle
The ∆ABC is a Right angle triangle, ∠B=90°. AB=p, BC=b & hypotenuse AC=h. The length of the Inradius of the triangle is ‘r’ then find the length of AI, where I is the Incenter of the triangle.
The length of the Inradius

In quadrilateral ALIN, ∠ALI+∠ANI=180° (Sum of opposite angles =180°)
So, ALIN is the Cyclic Quadrilateral.
Similarly, CMIN is also a Cyclic Quadrilateral.

Here, AI and CI are the diameters of the respective circles.
∆ALI ⩭ ∆ANI (Congruent Triangles)
AL=AN=p-r
Similarly, CM=CN=b-r
AC=AN+CN
h=p-r+b-r
h=p+b-2r
r=\frac{p+b-h}{2}.

In right angle ∆ALI,
AI²=AL²+LI² (Pythagoras Theorem)
=(p-r)²+r²
=(p-\frac{p+b-h}{2})^2+(\frac{p+b-h}{2})^2.
=(\frac{p-b+h}{2})^2+(\frac{p+b-h}{2})^2.
=\frac{1}{4}[(p-(b-h))^2+(p+(b-h))^2].
=\frac{2}{4}[p^2+(b-h)^2].
=\frac{1}{2}[(p^2+b^2)+h^2-2bh].
=\frac{1}{2}[2h^2-2bh].
AI=\sqrt{h×(h-b)}.
Similarly,
CI=\sqrt{h×(h-p)}.
The length of the Circumradius
The circumcenter of a Right angle triangle lies at the mid-point of its Hypotenuse so the hypotenuse act as the diameter of the circumcircle.
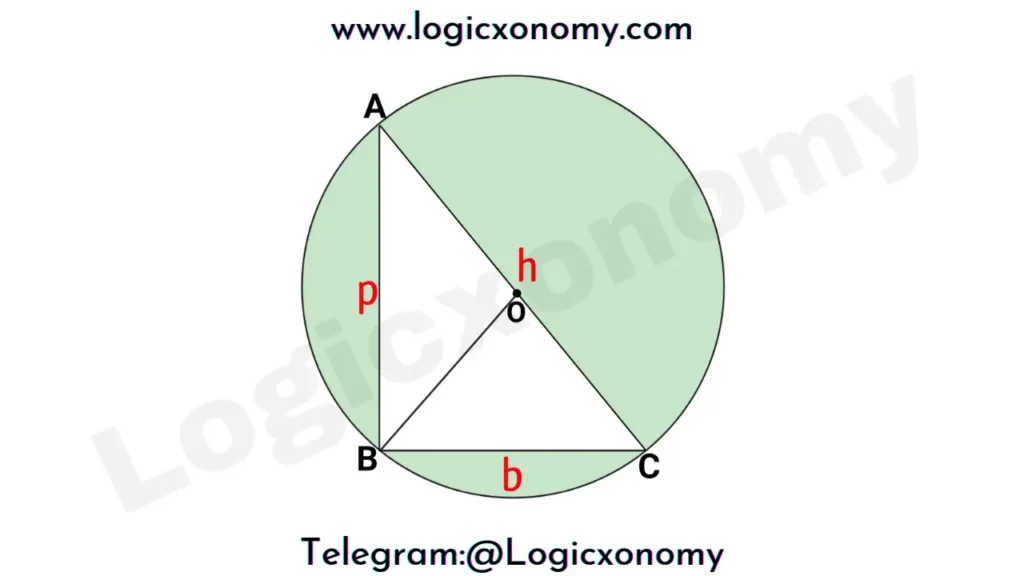
AO=OC=OB
Here, OB is one of the Medians of ∆ABC.
Now, The length of the Circumradius (R)=\frac{h}{2}
Routh’s Theorem of the Triangle: Click Here

