Here are some Calendar Problems with Solutions. The chapter on Calendar comes under logical reasoning and is one of the most confusing and difficult to understand for the students, but it will be one of the easiest chapters for you after learning all the concepts given.
There are two types of years in the Calendar System:
- Leap Year
- Non-Leap Year
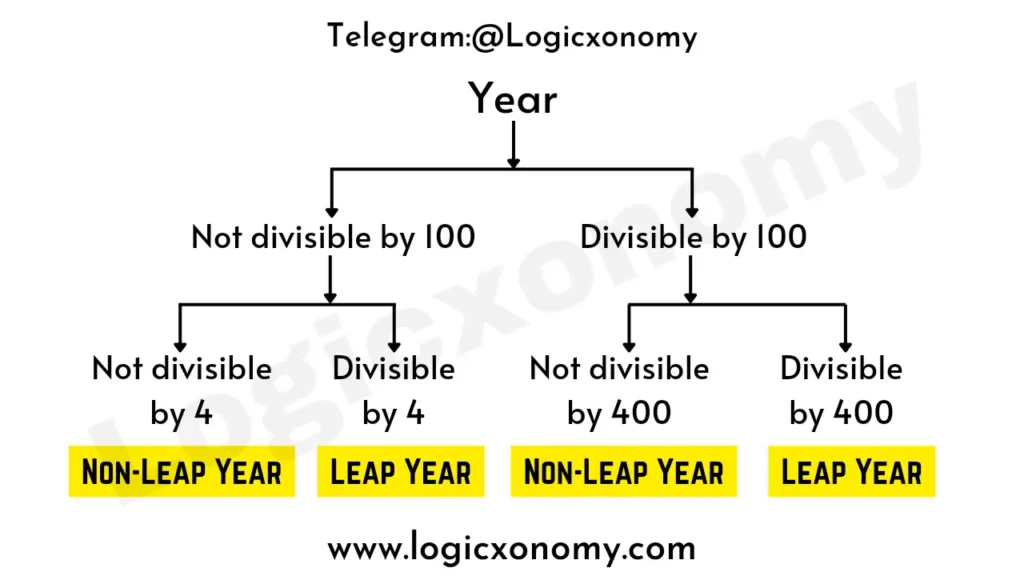
Leap Year
February has 29 days in a leap year, so the total number of days in such years is 366. A year that is divisible by both 100 and 400 or not divisible by 100 but divisible by 4 is called a leap year.
Non-Leap Year
A year that is not a leap year is called a non-leap year. There are 365 days in such years and only 28 days in February.
Note: The years 100 AD, 200 AD, 300 AD, 1800 AD, 1900 AD, etc are not Leap Years. 400 AD, 800 AD, 1200 AD, 1600 AD, and 2000 AD are Leap Years.
The Concept of odd days
The calendar system follows the concept of a 7-day week. Therefore, those extra days which can’t complete the cycle of a week are called odd days. Let, N be the total number of days, then
The number of Odd Days= N mod 7
Note: ‘mod’ is known as the Modulo Operator which produces the remainder of an integer division. In this case, the remainder when N is divided by 7. (Calendar Problems with Solutions)
Example: In a Leap year there 366 days means N=366
Number of odd days= 366 mod 7=2
It means a Leap Year has 2 Odd Days.
In the Non-Leap year, the Number of Odd Days= 365 mod 7=1
| Month | Days | Odd Days |
| January | 31 | 3 |
| February | 28 or 29 | 0 or 1 |
| March | 31 | 3 |
| April | 30 | 2 |
| May | 31 | 3 |
| June | 30 | 2 |
| July | 31 | 3 |
| August | 31 | 3 |
| September | 30 | 2 |
| October | 31 | 3 |
| November | 30 | 2 |
| December | 31 | 3 |
(A) From 1 AD to 100 AD:
Here, there are 100 years of which every fourth year is a leap year till 96 AD (Ex: 4, 8, 12, ….,96).
100 AD is not a leap year because it does not meet the conditions.
Total leap years= 24
Non-Leap Years= 76
Number of Odd Days= (24×2 +76×1) mod 7
=(3×2 +6×1) mod 7
=12 mod 7
=5
Note: 2 Odd Days in a Leap Year and 1 Odd Day in a Non-Leap year.
(B) From 101 AD to 200 AD: The number of Odd Days=5
(C) From 201 AD to 300 AD: The number of Odd Days=5
(D) From 301 AD to 400 AD:
Here, 400 AD is a leap year so we need to add 1 extra odd day to the 5. Therefore, the total number of odd days= 6
Finally, from 1 AD to 400 AD, the total number of odd days = (5+5+5+6) mod 7
= 21 mod 7
=0
Here Zero Odd Days means, the calendar repeats itself every 400 years. The calendar for 1 AD and 401 AD are identical. (Calendar Problems with Solutions)
Gregorian Calendar
The Gregorian calendar is an internationally accepted civil calendar also known as the Western or Christian calendar. (Calendar Problems with Solutions)
According to this Calender, the day on 1 January 0001 was Monday.
Here we give some numerical values for all the days of the week which are:
| Day | Numerical Value |
| Sunday | 0 |
| Monday | 1 |
| Tuesday | 2 |
| Wednesday | 3 |
| Thursday | 4 |
| Friday | 5 |
| Saturday | 6 |
Day Calculation from Date
Que 1: Find the Day on 14 September 1967.
Solution: 1967 is a Non-Leap Year. (Calendar Problems with Solutions)
Step 1: As we know, there are zero odd days in every 400 years so the total number of odd days from 1 AD to 1600 AD = 0 ………..(i)
Step 2: Now there are 5 odd days in each century i.e. 17th, 18th, and 19th century
Number of odd days= (5+5+5) mod 7= 1 …………(ii)
Step 3: Find the number of odd days from 1901 to 1966.
Number of leap years= 66/4= 16
Number of Non-Leap years= 66-16= 50
Number of Odd days= (16×2 +50×1) mod 7
=(2×2 +1×1) mod 7
=5 mod 7
=5 ……………(iii)
Step 4: Number of Odd days from January to August= (3+0+3+2+3+2+3+3) mod 7
=19 mod 7
=5 ……….(iv)
Number of Odd Days in next 14 days= 14 mod 7= 0 ……..(v)
Finally, the Total number of Odd Days= (0+1+5+5+0) mod 7
=11 mod 7
=4
Here, 4 represents Thursday.

Que 2: Find the Day on 25 April 1868.
Solution: 1868 is a Leap Year (there would be 29 days in February)
Step 1: Odd Days=0
Step 2: Odd Days in 17th and 18th Century= (5+5) mod 7=3
Step 3: Odd Days from 1801 to 1867
Number of leap years= 67/4= 16
Non-Leap years= 67-16=51
Odd Days=(16×2 +51×1) mod 7
=(2×2 +2×1) mod 7
=6 mod 7
=6
Step 4: Odd days in the rest of the days=(3+1+3+25) mod 7
=(7+4) mod 7
=11 mod 7
=4
Total number of Odd Days=(0+3+6+4) mod 7
=13 mod 7
=6
Here, 6 represents Saturday. (Calendar Problems with Solutions)
Multiple Choice Questions
Que 1: The day on 18/09/1977 was Sunday, A couple was married on this date. How many marriage anniversaries would fall on Sunday in the next 15 years?
(a) 1
(b) 2
(c) 5
(d) 7
Que 2: The Calendar of 1898 will repeat in which year? (Calendar Problems with Solutions)
(a) 1905
(b) 1903
(c) 1910
(d) None
Que 3: If the Republic Day of India was celebrated on a Sunday in 1996, then on which day the Independence day will be celebrated in 2036?
Note- Republic Day: 26 January and Independence Day: 15 August (Calendar Problems with Solutions)
(a) Monday
(b) Sunday
(c) Wednesday
(d) Friday
Que 4: If the first day of the Non-Leap year is Friday, then which will be the last of that year?
(a) Wednesday
(b) Friday
(c) Sunday
(d) Thursday
Que 5: What is the day of 1st January 1901? (Calendar Problems with Solutions)
(a) Sunday
(b) Tuesday
(c) Thursday
(d) Saturday
Que 6: Today is Thursday. The day after 59 days will be?
(a) Sunday
(b) Thursday
(c) Saturday
(d) Monday
Que 7: Saturday was a holiday for Republic Day. Shivratri is again a holiday on the 14th of the next month. What day was it on the 14th?
Note: Republic Day of India is celebrated on 26 January each year. (Calendar Problems with Solutions)
(a) Friday
(b) Tuesday
(c) Thursday
(d) Monday
Que 8: If the seventh day of a month is three days earlier than Friday, What day will it be on the nineteenth day of the month?
(a) Sunday
(b) Thursday
(c) Monday
(d) Friday
Que 9: The calendar for 1990 was the same as of …
(a) 1993
(b) 1996
(c) 2000
(d) 1997
Que 10: If the third day of a month is Monday, then which of the following will be the fifth day from the 21st of that month? (Calendar Problems with Solutions)
(a) Wednesday
(b) Thursday
(c) Sunday
(d) Monday
Que 11: If it was Saturday, December 17, 1899, then what will be the day on December 22, 1901?
(a) Friday
(b) Saturday
(c) Monday
(d) Wednesday
Que 12: If the national day of a country was celebrated on the 4th Saturday of a month, then find the date of celebration, if the first day of that month is Tuesday. (Calendar Problems with Solutions)
(a) 22
(b) 26
(c) 29
(d) 25
Que 13: The first day of a leap year was Wednesday, then what day of the week was it on 31st December in that year?
(a) Thursday
(b) Sunday
(c) Wednesday
(d) Saturday
Que 14: Find the number of days from 26th January 2011 to 23rd September 2011 (both days are included).
(a) 214
(b) 238
(c) 241
(d) 253
Que 15: If the 4th Saturday of a month was the 22nd day, then what was the 13th day of that month? (Calendar Problems with Solutions)
(a) Friday
(b) Sunday
(c) Thursday
(d) Monday
Que 16: If 15th June falls 3 days after tomorrow which is Friday, then on which day of the week will the last date of the month fall?
(a) Monday
(b) Tuesday
(c) Wednesday
(d) Thursday
Que 17: If 27 March 1995 was a Monday, then what was the day of the week on 1 November 1994?
(a) Wednesday
(b) Sunday
(c) Tuesday
(d) Saturday
Que 18: Which of the following is a leap year?
(a) 2800
(b) 1800
(c) 2600
(d) All of the above
Que 19: How many Mondays are there in a month of a particular year if the month ends on Wednesday? (Calendar Problems with Solutions)
(a) 4
(b) 5
(c) 3
(d) None
Que 20: Find the day on 16 September 1979.
(a) Monday
(b) Sunday
(c) Friday
(d) Thursday
Que 21. What was the year of birth of Mrs. Rao’s son, given that they were married on 13th April 1893 and their son was born on the day of their first wedding anniversary, which first fell on a Sunday?
(a) 1899
(b) 1902
(c) 1905
(d) 1911
Answer Key:
1.b, 2.c, 3.b, 4.b, 5.b, 6.a, 7.c, 8.a, 9.b, 10.a, 11.b, 12.b, 13.a, 14.c, 15.c, 16.b, 17.c, 18.a, 19.d, 20.b, 21.b
Solutions:
1) From 1978 to 1992⇨ 15 years
Odd Days⇨ [1, 1, 2, 1, 1, 1], [2, 1, 1, 1, 2], 1, 1, 1, 2
The sum of first 6 terms= 7 means 0 odd days ⇨1983
The sum of next 5 terms= 7 means 0 odd days ⇨1988
The next two anniversaries fell in 1983 and 1988.
2) After 1898 the years 1904 and 1908 are Leap years
Odd Days in years from 1898 to 1909⇨ 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1
The Sum of odd days= 14 mod 7=0
It means the Calendar of 1910 is the same as that of 1898.
3) From 26 January 1996 to 26 January 2036, There are 40 complete years.
In this period, 10 will be leap years and the remaining 30 years will be non-leap years.
The number of Odd days= (10×2+30×1) mod 7=1
Now we have to calculate the number of odd days from 27 January 2036 to 15 August 2036.
The number of Odd days=(5+1+3+2+3+2+3+15) mod 7=6
Total Odd Days= (6+1) mod 7=0
That is, 26 January 1996 and 15 August 2036 are Sundays.
4) The number of Odd days in a Non-Leap year= 1 (Calendar Problems with Solutions)
Example: If 1st Jan 2003 is Friday then 1st Jan 2004 will be Saturday
Thus, 31st December 2003 will be Friday
5) Number of Odd days= (0+5+5+5+1) mod 7=2
Here 2 represents Tuesday.
6) The number of Odd days= 59 mod 7=3 (Calendar Problems with Solutions)
Thursday +3⇒ Sunday
7) The number of Odd days= (5+14) mod 7=5
Saturday +5⇒ Thursday
8) 7 is 3 days earlier than Friday means the date on Friday is 10.
The number of Odd days after 10, till 19= 9 mod 7=2
Friday +2⇒ Sunday
9) Odd days from 1990 to 1995= (1+1+2+1+1+1) mod 7=0
So, the calendar of 1990 and 1996 are identical.
10) The third day of the Month ⇒Monday
The fifth date after 21 ⇒21+5=26
Number of days= 26-3=23
The number of Odd days= 23 mod 7=2
So, there will be Wednesday on the 26th date of the month.
11) 17 Dec 1899 to 17 Dec 1901⇒ Odd days=1+1=2
The rest Odd days=5 (Calendar Problems with Solutions)
Total Odd day= (2+5) mod 7=0
The correct answer is ‘Saturday’.
12) 1st day of the month ⇒Tuesday
so the first Saturday will fall on the 5th.
The date on 4th Saturday= 5+21=26
13) Example: Let, 1 January 2000 ⇒Wednesday
The number of Odd days in a leap year=2
Then 1 January 2001 ⇒Friday
So, the day on 31 December ⇒Thursday
14) Total number of days= 6+28+31+30+31+30+31+31+23= 241
15) Date on 4th Saturday⇒ 22 (Calendar Problems with Solutions)
22-14=8
So, the day on the 8th of this month⇒ Saturday
13-8=5
Day on 13th of this month⇒ Saturday+5⇒ Thursday
16) Tomorrow is Friday so the day after 3 days (15 June) will be Monday.
The number of Odd days upto 30 June from 15th June= 15 mod 7=1
So the day on the last day of the month is Tuesday.
17) The number of Odd days from 1 November 1994 to 27 March 1995= (29+3+3+0+27) mod 7=6
In this question, the years are in reverse order.
So, either subtract 6 or add 1 to find the day.
Monday+1⇒ Tuesday (Calendar Problems with Solutions)
18) 2800 is divisible by both 100 and 400.
19) The exact month is not mentioned. It can be a month of 28, 29, 30, or 31 days.
20) 16 September 1979
The number of Odd days= [0 +(5+5+5) +(19×2+59×1) +(3+0+3+2+3+2+3+3+16)] mod 7
=[1+6+0] mod 7
=0
So it’s Sunday.
21) The day on 13th April 1893⇒Thursday
[5+5+{23×2+69×1}+{3+0+3+13}] mod 7= 4
Now, for Sunday, the number of odd days should be equal to 3
4+3=7 or 0
1894⇒ 1
1895⇒ 1
1896⇒ 2
1897⇒ 1
1898⇒ 1
1899⇒ 1
1900⇒ 1
1901⇒ 1
1902⇒ 1
Total odd days= 3 (Calendar Problems with Solutions)
So, the year of birth= 1902
Permutation and Combination: Click Here

