Geometry Formulas (50 Interesting exam Hacks)

In this chapter, we will discuss some interesting geometry formulas and frequently asked questions about geometry that every student should know.

Why is the Volume of the Cone one-third of the Cylinder

As we know, Both cylinder and cone are made up of circular plates arranged one above the other. Here the width of each circular plate inside both shapes is dx (very small).

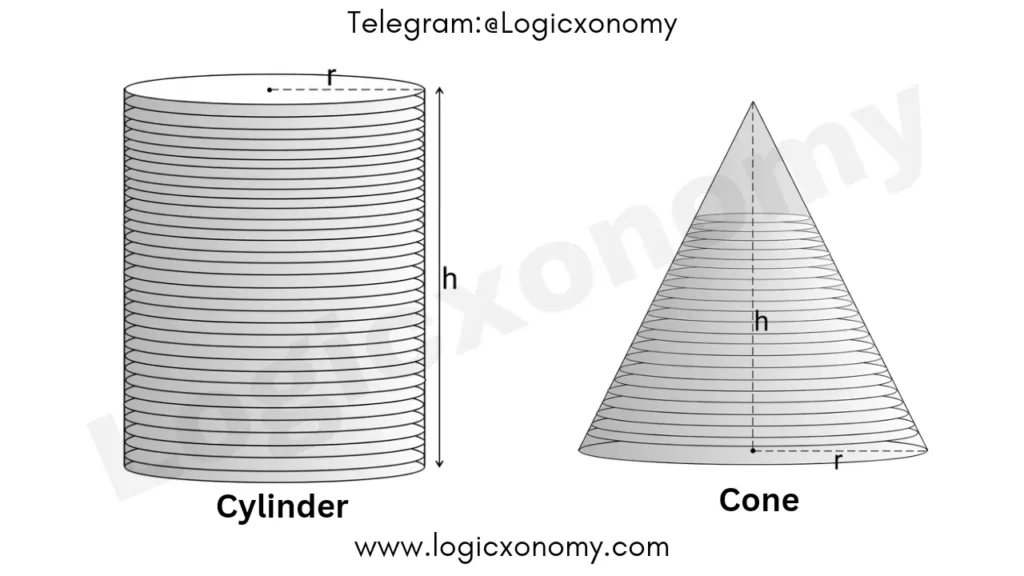
In the case of a cylinder, the radius (r) of all the plates is the same from bottom to top but in the case of the cone, the radius of the plates decreases continuously from bottom to top and ends at zero at the top.

So, the Volume of each plate (Very Small)= Base Area × Height

dv=𝜋r².dx   …………(i)

The volume of the Cylinder= Sum of the Volumes of all the plates 

\int dv=\int_{0}^{h}\pi r^{2}dx.

v=\pi r^{2}.\int_{0}^{h}dx.

v=\pi r^{2}[h-0].

v=\pi r^{2}h.

Volume of the Cylinder= 𝝅r²h   ……….. (ii) 

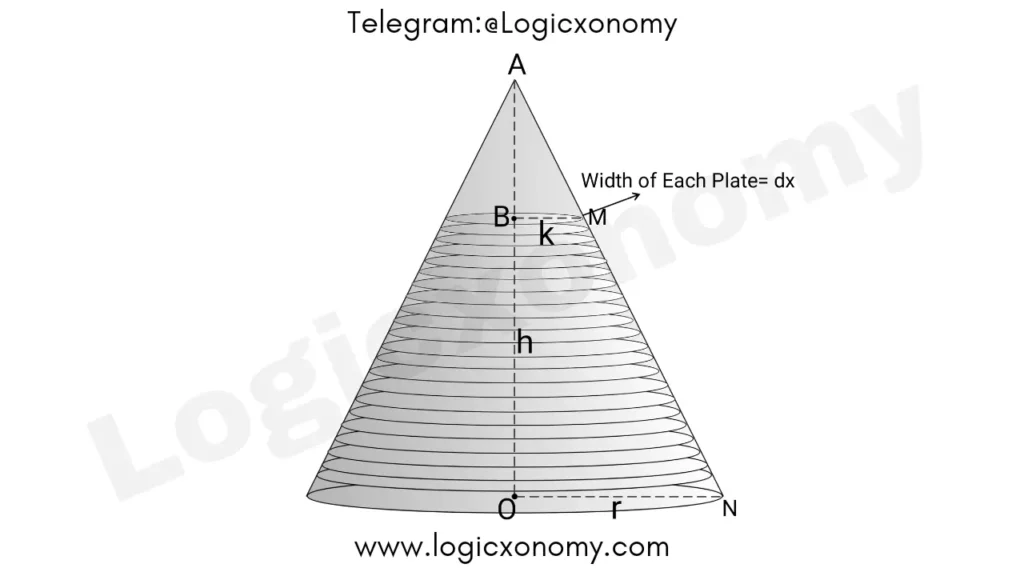
In the case of Cone, △ABM~△AON (Similar Triangles)

So, \frac{AB}{AO}=\frac{BM}{ON}.

Note: Here AB is the distance of the arbitrary plate from the Apex of the Cone. k is the radius of the plate (The radius of all the plates are different)

In the case of the bottom plate, x=h

Here x is associated with dx (The width of each plate)

\frac{x}{h}=\frac{k}{r}.

k=\frac{rx}{h} ………(iii)

The volume of the Cone= Sum of the Volumes of all the plates 

\int dv=\int_{0}^{h}\pi k^{2}dx.

v=\pi \int_{0}^{h}(\frac{rx}{h})^{2}dx.

v=\pi \frac{r^{2}}{h^{2}}\times \int_{0}^{h}x^{2}dx.

v=\frac{\pi r^{2}}{h^{2}}\times \frac{1}{3}(h^{3}-0).

v=\frac{1}{3}\pi r^{2}h.

The volume of the Cone= \frac{1}{3}\pi r^{2}h.

So, we can say the volume of the cone is one-third of the volume of a Cylinder of the same height and base radius. (Geometry Formulas)

Relation between the Volumes of a Prism and a Pyramid

Que: Why is the volume of a pyramid one-third that of a prism of equal base and height?

Ans: If you turn the circular base of a Cylinder into a polygon, it becomes a Prism. Similarly, If you turn the circular base of a cone into a polygon, it becomes a Pyramid.

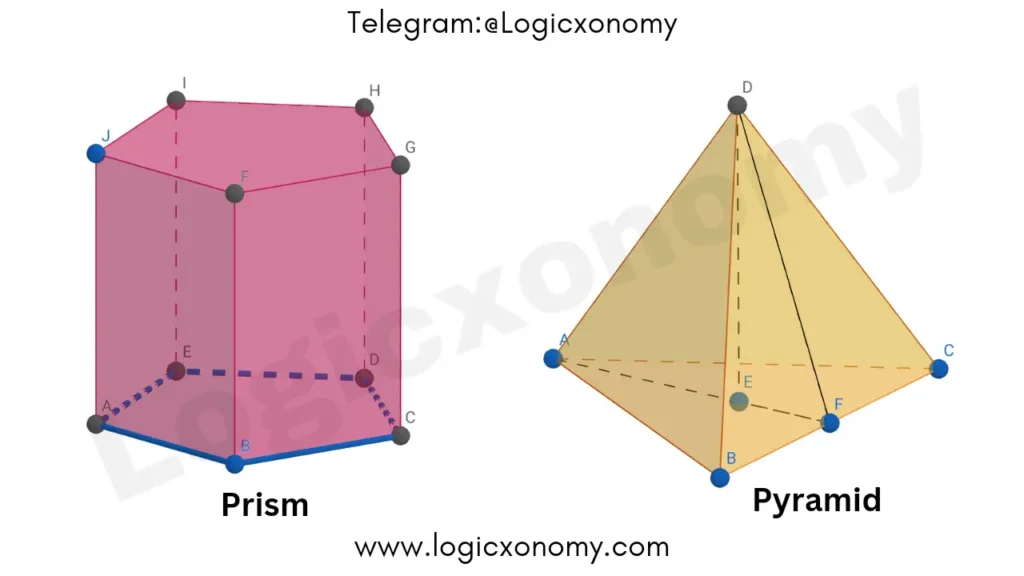
So, all the concepts of Cylinder and Cone are also applicable here.

In the case of the same base and height, the volume of a Pyramid is always one-third of the volume of a Prism.

The volume of the Sphere

A sphere is made of thin circular discs arranged one above the other as shown in the figure. Here the width of the disc is dy (very small), its distance from the center of the sphere is y and the radius is x. The radius of the Sphere is R.

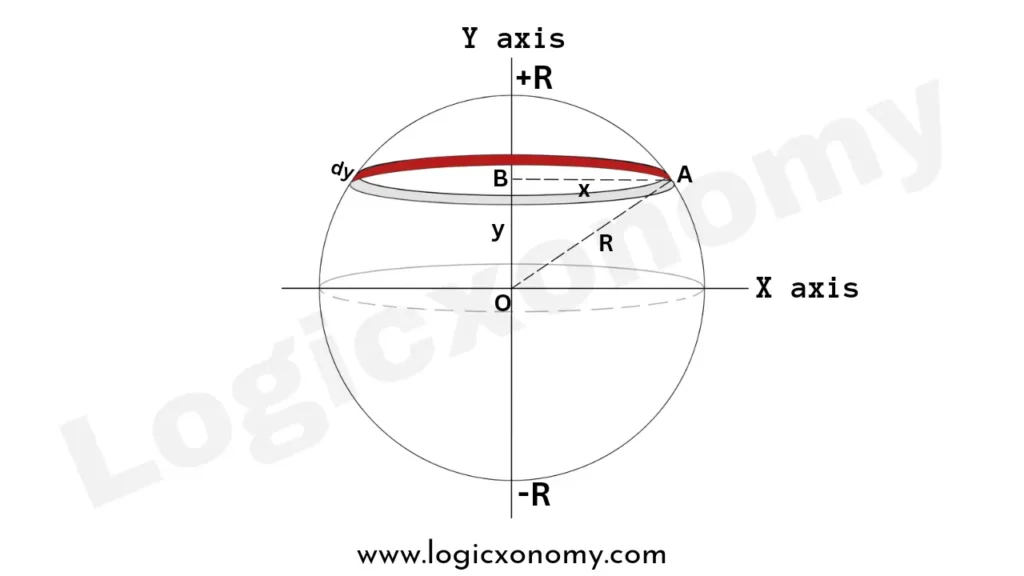
Since this disc is very thin, it is like a cylinder. Thus, the volume of the disc = Base Area× Height

dv=𝜋x².dy……..(i)

Apply Pythagorean theorem, x²+y²=R² (Geometry Formulas)

x²=R²-y² ……….(ii)

So, dv=𝜋(R²-y²).dy

Integrate both sides: (V is the volume of the whole sphere)

\int dv=\int_{-R}^{+R}\pi (R^{2}-y^{2}).dy.

V=\pi\times [R^{2}y-\frac{y^{3}}{3}]_{-R}^{+R}.

V=\pi\times [(R^{3}-\frac{R^{3}}{3})-(-R^{3}-\frac{-R^{3}}{3})].

V=\frac{4}{3}\pi R^{3}.

Surface Area of the Sphere

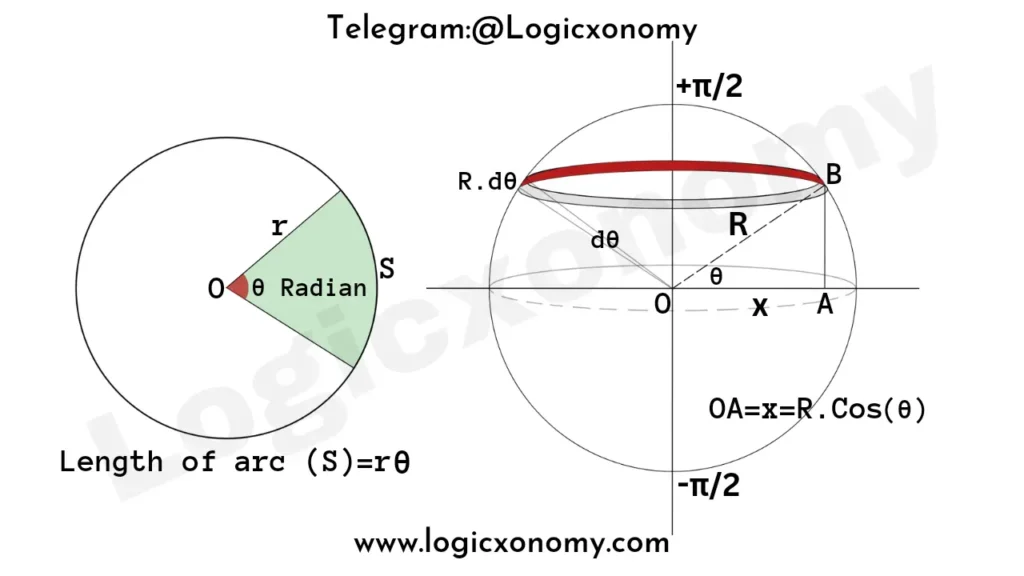
The boundary of the thin strip is curved, so its breadth (arc length), dy = R.dθ

In △OAB, OA=x=R.Cos(θ)

So, the curved surface area of the strip= Circumference of the base× height

ds=2𝜋x.dy

ds=2𝜋R.Cos(θ).R.dθ

ds=2𝜋R².Cos(θ).dθ 

Integrate both sides: (S is the total surface area of the Sphere)

\int ds=\int_{-\frac{\pi}{2}}^{+\frac{\pi}{2}}2\pi R^{2}.Cos(\theta).d\theta.

S=2\pi R^{2}\times [Sin(\theta)]_{-\frac{\pi}{2}}^{+\frac{\pi}{2}}.

S=2\pi R^{2}\times [Sin(\frac{\pi}{2})-Sin(-\frac{\pi}{2})].

S=2\pi R^{2}\times [1-(-1)].

S=4\pi R^{2}.

Note: If a sphere of radius R is contained in a cylinder of base radius R and height 2R, then in this case the lateral surface area of ​​the cylinder is equal to the total surface area of ​​the sphere. (Geometry Formulas)

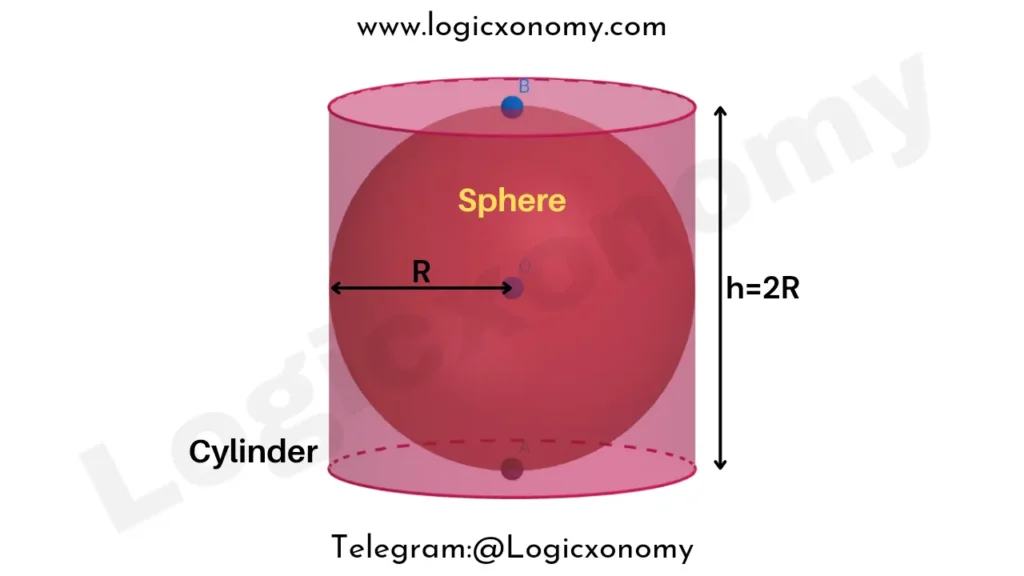
Height of Cylinder, h=2R

The lateral surface area of the cylinder= 2𝜋Rh

=2𝜋R×2R

=4𝜋R²

The volume of the largest Cylinder inscribed in a Sphere

The radius of the Sphere is R, the base radius of the Cylinder is r and the height is h. Point O is the center of the Sphere.

Let, OA=x

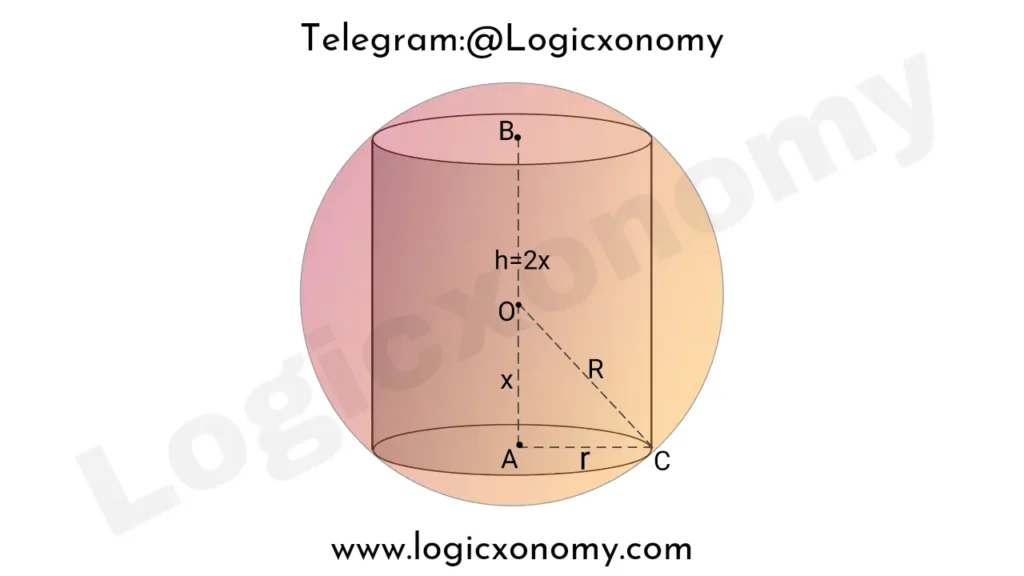
Apply Pythagoras theorem in △OAC,

x²+r²=R² ………(i)

h=2x

The volume of the Cylinder (V)= 𝜋r²h

V= 𝜋r².(2x)

V=2𝜋.(R²-x²).x 

V=2𝜋.(R²x-x³) ………(ii)

Differentiate both sides,

\frac{dV}{dx}=2\pi.(R^2-3x^2).

Again differentiate both sides,

\frac{d^{2}V}{dx^{2}}=-12\pi x ……. (Negative)

So, for the maximum value of x, Put \frac{dV}{dx}=0.

x=\frac{R}{\sqrt{3}} ………(iii)

h=2x=\frac{2R}{\sqrt{3}}.

r=\sqrt{R^2-x^2}=\sqrt{\frac{2}{3}}\times R.

The Maximum Volume of the Cylinder, V=\pi r^{2}h.

V=\pi\times \frac{2}{3}R^{2}\times \frac{2R}{\sqrt{3}}.

V=\frac{4\pi}{3\sqrt{3}}\times R^{3}.

The volume of the largest Cone inscribed in a Sphere

The radius of the Sphere is R, the base radius of the Cone is r and the height is h. Point O is the center of the Sphere. (Geometry Formulas)

Let, OA=x

Apply Pythagoras theorem in △OAC,

x²+r²=R² ………(i)

h=R+x

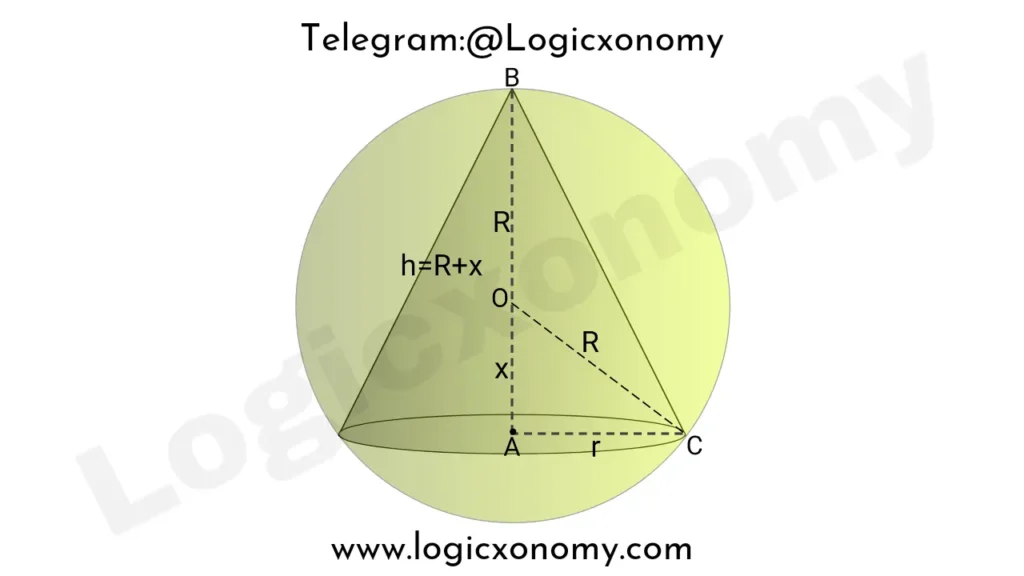
The volume of the Cone (V)= \frac{1}{3}\pi r^{2}h.

V=\frac{1}{3}\pi\times (R^{2}-x^{2})\times (R+x).

V=\frac{1}{3}\pi\times (R^{3}+R^{2}x-Rx^{2}-x^{3}).

Differentiate both sides,

\frac{dV}{dx}=\frac{1}{3}\pi\times (0+R^{2}-2Rx-3x^{2}).

Again differentiate both sides,

\frac{d^{2}V}{dx^{2}}=\frac{1}{3}\pi\times (-2R-6x)     …… (Negative)

So, for the maximum value of x, Put \frac{dV}{dx}=0.

R^{2}-2Rx-3x^{2}=0.

R^{2}-3Rx+Rx-3x^{2}=0.

R.(R-3x)+x.(R-3x)=0.

(R+x).(R-3x)=0.

So, (R-3x)=0.

x=\frac{R}{3}.

r=\sqrt{R^{2}-x^{2}}=\frac{2\sqrt{2}}{3}\times R.

h=R+x=\frac{4}{3}\times R.

The Maximum Volume of Cone, V=\frac{1}{3}\pi r^{2}h.

V=\frac{1}{3}\pi\times\frac{8}{9}R^{2}\times\frac{4}{3}R.

V=\frac{32}{81}\pi R^{3}.

The ratio between the Volumes of the Cylinder and the Cone= \frac{4\pi}{3\sqrt{3}} R^{3} :\frac{32}{81}\pi R^{3}.

⇒ \frac{1}{\sqrt{3}} : \frac{8}{27}.

⇒ \frac{1}{\sqrt{3}} : \frac{8}{9\times\sqrt{3}\times\sqrt{3} }.

⇒ 1 : \frac{8}{9\times\sqrt{3}}.

Multiply with 9√3,

⇒ 9\sqrt{3} :8.

Maxima and Minima from Calculus

Let, f(x) be a function of x and y=f(x)

Here, the derivative of function \frac{dy}{dx} is geometrically represented as the slope of the curve. The slope is positive if the function is increasing, Zero at the maximum or minimum, and negative just after the maximum.

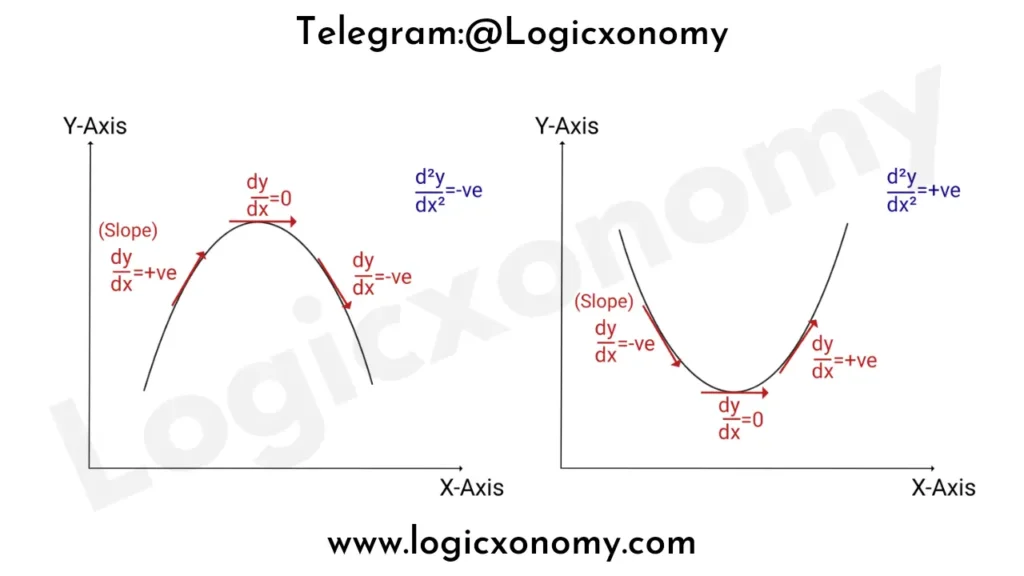
The second derivative \frac{d^{2}y}{dx^{2}} is the rate of change of the derivative. If the second derivative is negative at a critical point, then the critical point is a local maximum. If it’s positive, the critical point is a local minimum.

If \frac{d^{2}y}{dx^{2}}<0, the graph is bending downward (The curve is concave down)

If \frac{d^{2}y}{dx^{2}}>0, the graph is bending upward (The curve is concave up)

Spheres in a Cone

An infinite number of spheres are placed one above the other inside a right circular cone as shown in the figure. Given, the apex angle of a cone is 60° and the radius of the base is 5 cm. Find the sum of the volumes of all the spheres.

Let the lengths of the radii of the spheres be r₁, r₂, and r₃. B, C, and D are their centers. Line AL is tangent to the circles, so radii DE, CF, and BG are perpendicular to AL.

∠LAM=2x°

Draw, GI and FH Parallel to AD so ∠GAB=∠FGI=∠EFH=x°

GI=BC=r₂+r₃

FH=CD=r₁+r₂

EH=ED-HD=ED-FC=r₁-r₂

FI=FC-IC=FC-GB=r₂-r₃

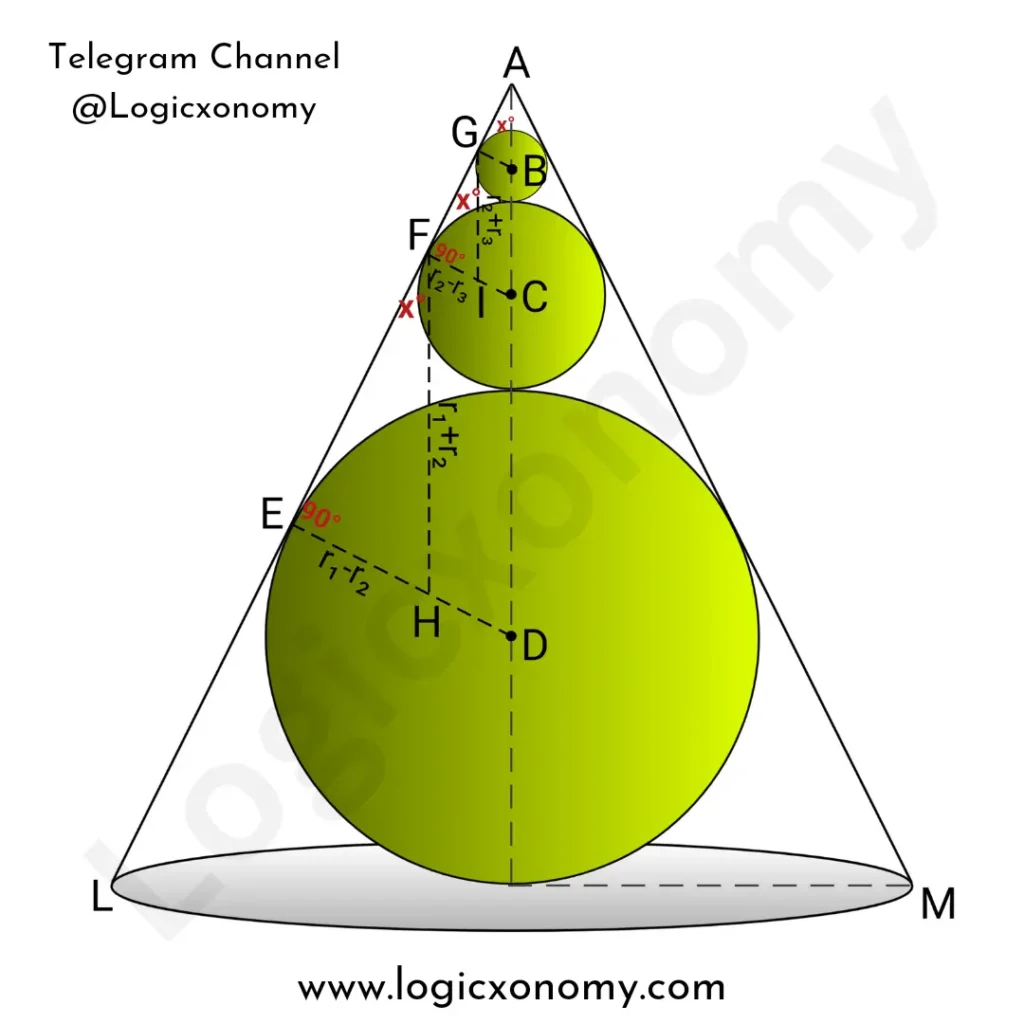
In right angle △EFH, 

Sin(x°)=\frac{EH}{FH}=\frac{r_{1}-r_{2}}{r_{1}+r_{2}}  ……….(i)

In right angle △FGI, 

Sin(x°)=\frac{FI}{IG}=\frac{r_{2}-r_{3}}{r_{2}+r_{3}}  ……….(ii)

From equations (i) and (ii):

\frac{r_{1}-r_{2}}{r_{1}+r_{2}}=\frac{r_{2}-r_{3}}{r_{2}+r_{3}}.

Apply componendo and dividendo rule:

\frac{(r_1-r_2)+(r_1+r_2)}{(r_1-r_2)-(r_1+r_2)}=\frac{(r_2-r_3)+(r_2+r_3)}{(r_2-r_3)-(r_2+r_3)}.

\frac{2r_1}{-2r_2}=\frac{2r_2}{-2r_3}.

\frac{r_1}{r_2}=\frac{r_2}{r_3} ……….(iii)

This means that r₁, r₂, and r₃ are in geometric progression (GP series)

Let, r₁=a

r₂=ar

r₃=ar²

Here r is the common ratio of the GP series. (Geometry formulas)

Now, Substitute these values ​​into equation (i):

Sin(x°)=\frac{a-ar}{a+ar}=\frac{1-r}{1+r}.

According to question 2x=60 so x=30

Sin(30°)=\frac{1-r}{1+r}.

\frac{1}{2}=\frac{1-r}{1+r}.

2-2r=1+r.

r=\frac{1}{3} ………(iv)  

Hence the radii of all the spheres are a, ar, ar², ar³, ar⁴, ar⁵,……..

⇒ a, \frac{a}{3}, \frac{a}{3^2}, \frac{a}{3^3}, \frac{a}{3^4}, ……..

The sum of the volumes of Spheres (V)= \frac{4}{3}\pi (r_1)^3+\frac{4}{3}\pi(r_2)^3+\frac{4}{3}\pi(r_3)^3+……..

V= \frac{4}{3}\pi.a^3\times (1+\frac{1}{3^3}+\frac{1}{3^6}+\frac{1}{3^9}+.......).

Apply Formula for Sum of GP Series

V= \frac{4}{3}\pi.a^3\times \frac{1}{1-\frac{1}{3^3}}.

V= \frac{4}{3}\pi.a^3\times \frac{27}{26}.

V=\frac{18}{13}\pi.a^3 …………..(v)

Since △ALM is a isosceles triangle (AL=AM) and ∠LAM=60°

Therefore △ALM is an Equilateral triangle.

The length of the side of the equilateral triangle (k)= 2×Base radius of Cone

k=2×5=10 cm

The area of the triangle (△)= \frac{\sqrt{3}}{4}.k^2=25\sqrt{3} cm²

The semiperimeter of the triangle (s)= \frac{10+10+10}{2}=15 cm

The length of the inradius of △ALM, which is also the radius of the largest circle (r₁= a)=\frac{\triangle}{s}.

a=\frac{25\sqrt{3}}{15}=\frac{5}{\sqrt{3}} cm

V=\frac{18}{13}\pi.a^3 …………..(v)

V=\frac{18}{13}\pi.\frac{125}{3\sqrt{3}}.

V=\frac{750.\pi}{13\sqrt{3}} cm³

Note: GP Series⇒x, xr, xr²,xr³,xr⁴,xr⁵,…..

First term= x

Common ratio= r (Here r<1)

The sum of the Infinite Terms= \frac{x}{1-r}.

Balls in a Cone (Ice Cream Cone Problem)

There are four balls in a cone as shown in the figure, whose radii are in increasing order r₁,r₂,r₃, and r₄. If the apex angle of the cone is 90°, then find the ratio of r₁ and r₄.

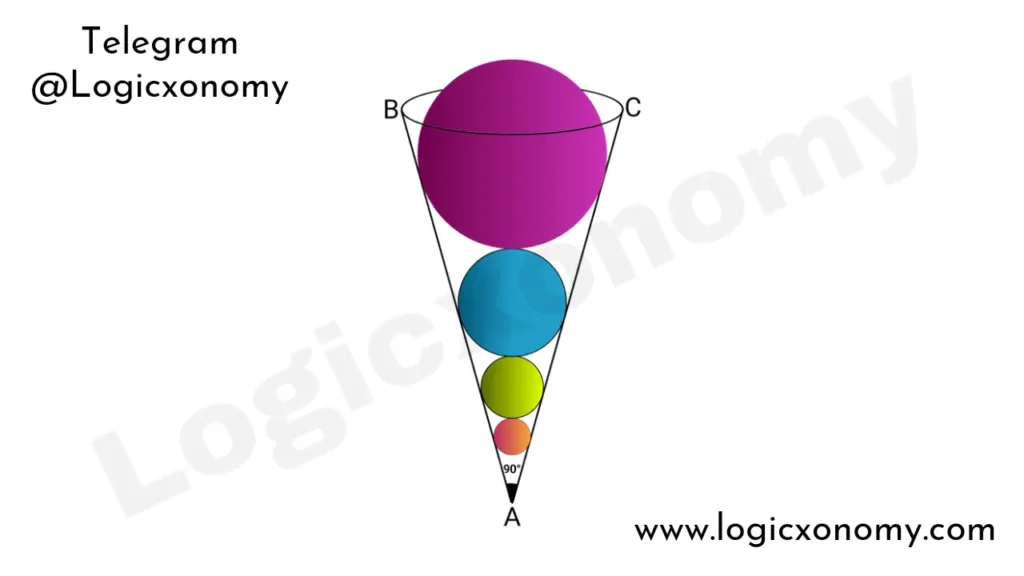
According to the previous concept the given radii are in geometric progression. Let r₁=a units, and the common ratio is ‘r’ (r>1).

r₁=a, r₂=ar, r₃=ar², and r₄=ar³

Given 2x=90

x=45

So, Sin(45°)=\frac{r_2-r_1}{r_2+r_1}.

\frac{1}{\sqrt{2}}=\frac{r-1}{r+1}.

r+1=\sqrt{2}.r-\sqrt{2}.

r=\frac{\sqrt{2}+1}{\sqrt{2}-1}.

Rationalize the denominator:

r=\frac{\sqrt{2}+1}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1}.

r=3+2\sqrt{2}.

So, r_1:r_4=1:(3+2\sqrt{2})^{3}.

Geometry Basics: Click Here

More Concepts are Coming Soon…