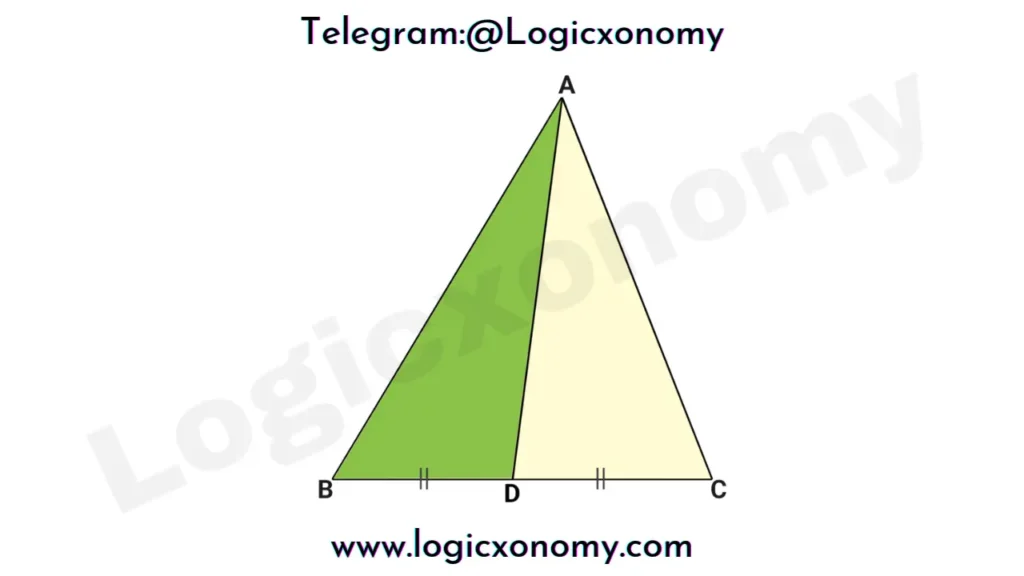
The point of intersection of all three Medians of the triangle is called the ‘Centroid’ of the triangle. The Median of a triangle is a line segment joining a vertex to the midpoint of its opposite side, thus bisecting the side.
The Median divides a triangle into two parts of equal areas. Here Area of ∆BAD =Area of ∆DAC.
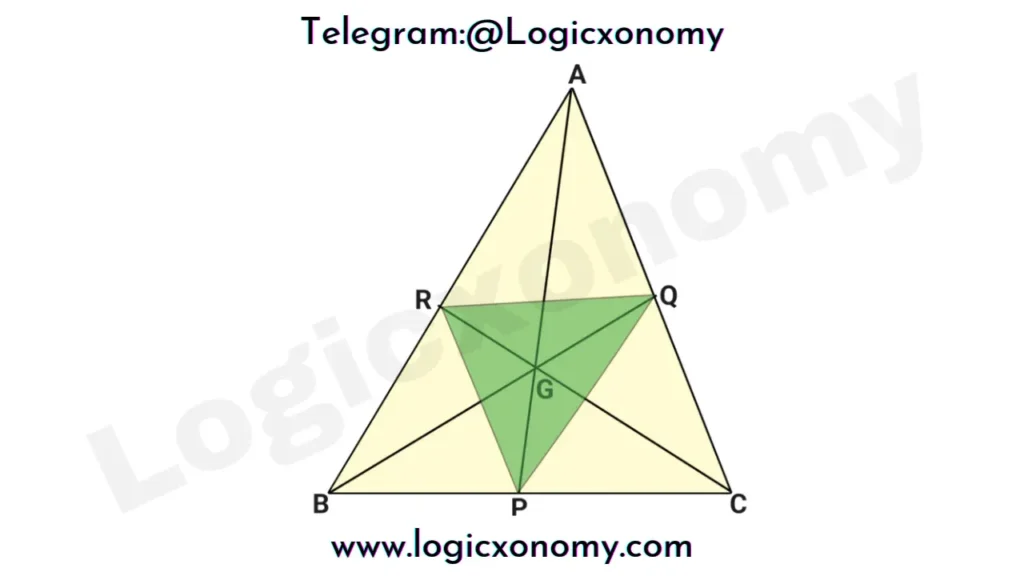
All the Medians of a triangle are concurrent (intersect at a single point), the point of concurrence is called the Centroid of the triangle. The Centroid always lies inside the triangle.
- Finding the centroid of a triangle: The centroid divides each median in the ratio of 2:1
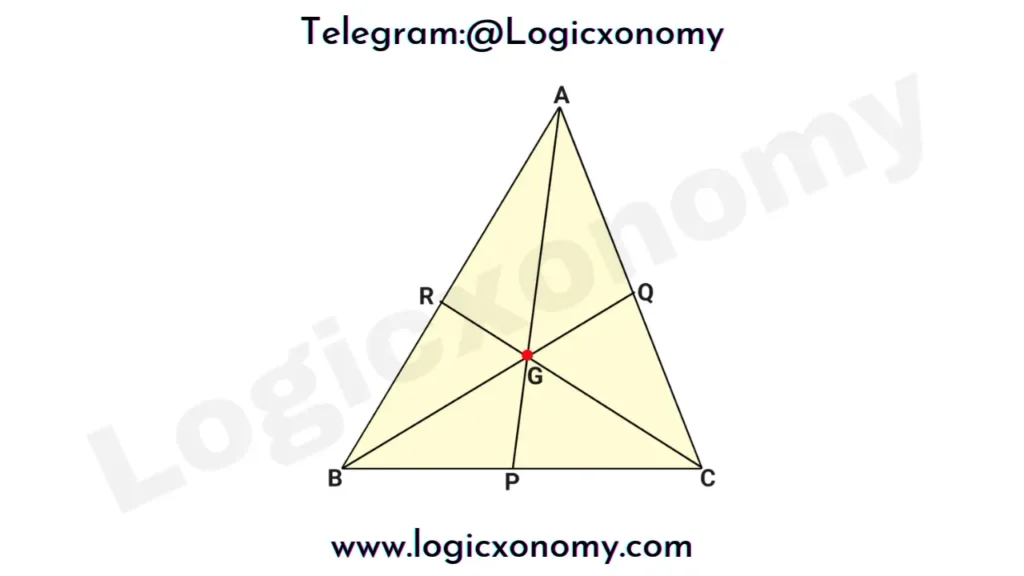
Here AG:GP=BG:GQ=CG:GR=2:1
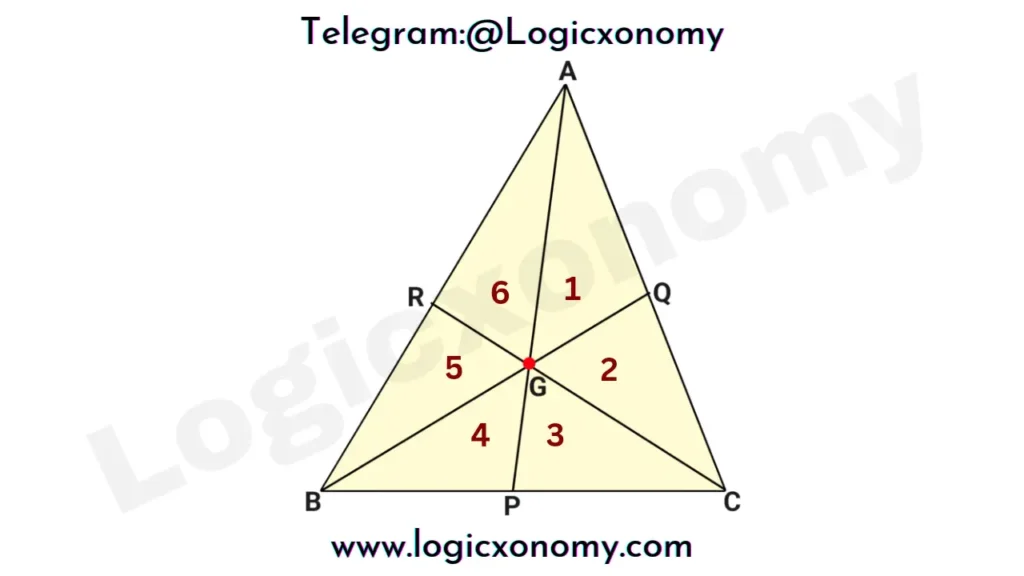
- All the medians divide a triangle into 6 parts of equal areas.
The Centroid and the Center of Gravity
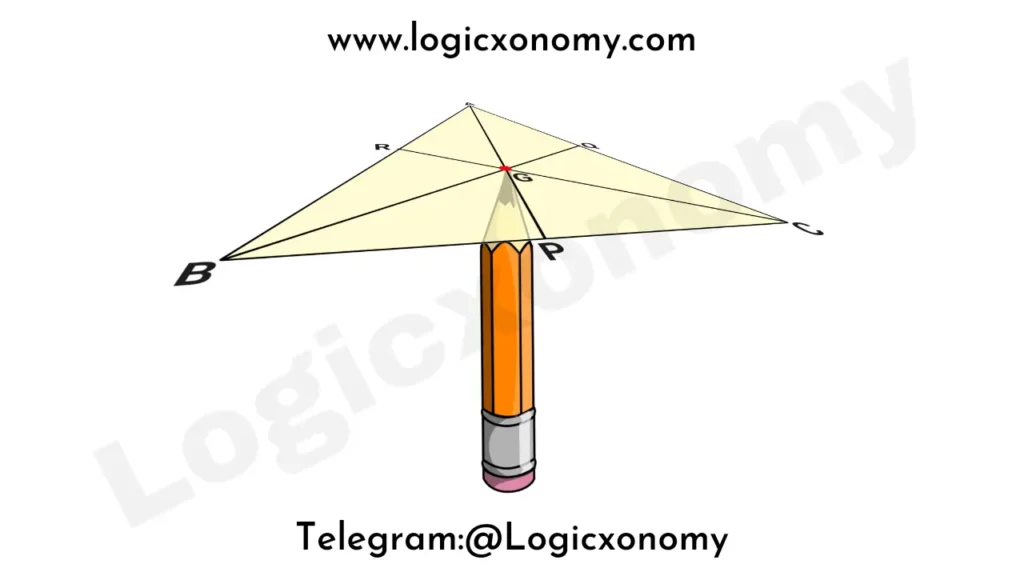
A homogeneous triangular sheet can be balanced on its Centroid. This means that the triangle is stabilized in a horizontal position when you place its Centroid on the tip of a Pencil.
In a homogeneous object, the density of matter is evenly distributed throughout its body.
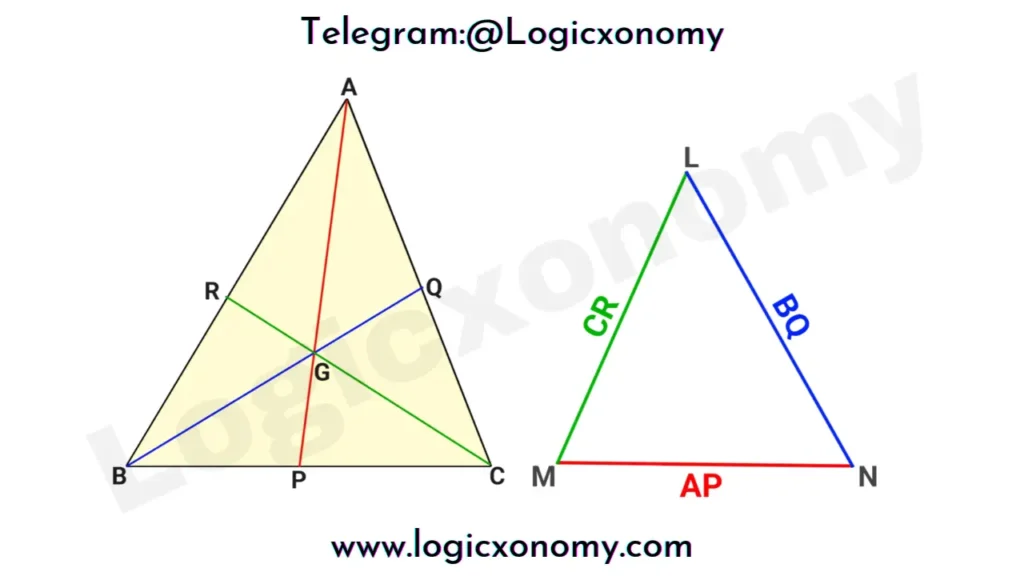
The triangle made by Medians
Find the area of the triangle when the lengths of its medians are given.
Here, Area of ∆ABC: Area of ∆LMN=4:3
Step 1: Draw a line PD=GP, by extending the line AP.
Let AP=3x, BQ=3y & CR=3z
Note: The Centroid divides each median in the ratio of 2:1
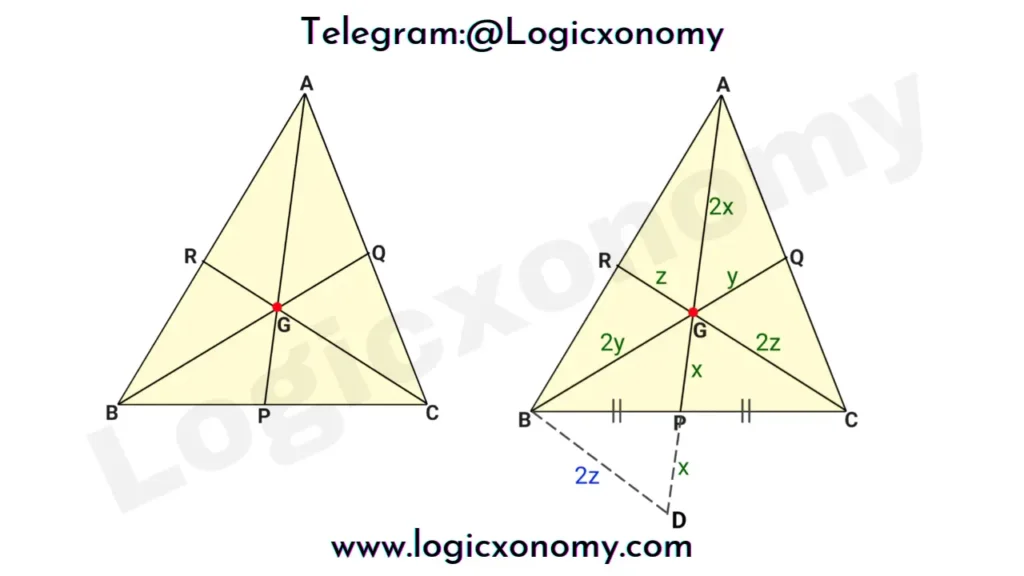
∆BPD ⩭ ∆CPG (Congruent Triangles)
∠BPD=∠CPG (Vertically Opposite)
BP=PC & GP=PD
As we know that all the medians divide a triangle into 6 parts of equal areas.
If the area of ∆ABC=6 unit
Then the area of ∆DBG=2 unit
Thus, the area of ∆ABC=3×area of ∆DBG
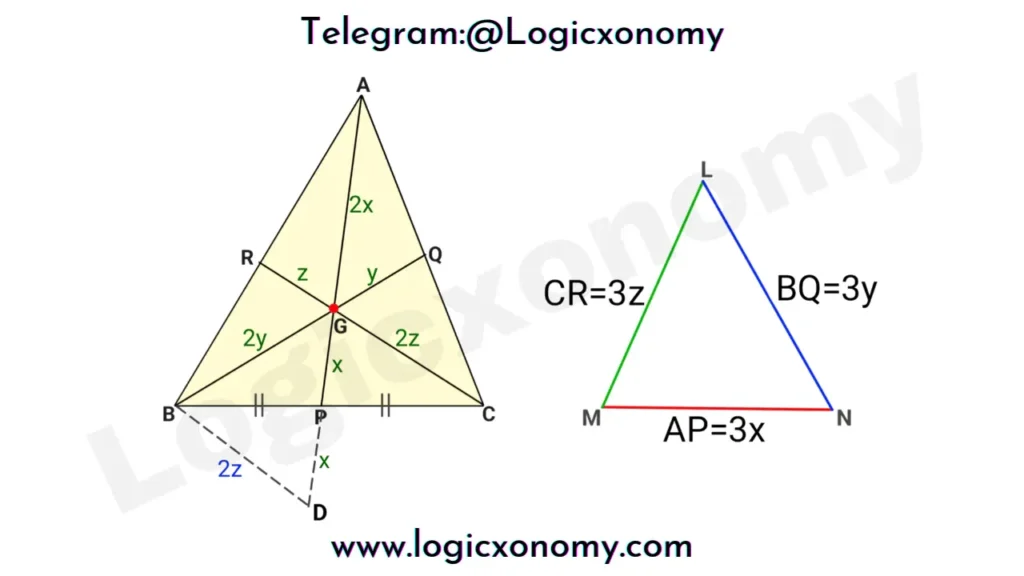
Now, Since ∆DBG ~ ∆MLN (Similar)
Note: Ratio of respective sides=2:3
So, the area of ∆DBG: area of ∆MLN=2²: 3²=4:9
The area of ∆DBG=4/9×area of ∆MLN
1/3×area of ∆ABC=4/9×area of ∆MLN
Area of ∆ABC=4/3×area of ∆MLN
Right angle property of Medians
In ∆ABC, G is the Centroid of the triangle. If AG=BC then find the value of ∠BGC.
Let, AP=3x
Then AG=2x, GP=x (Property), and BC=2x (Given)
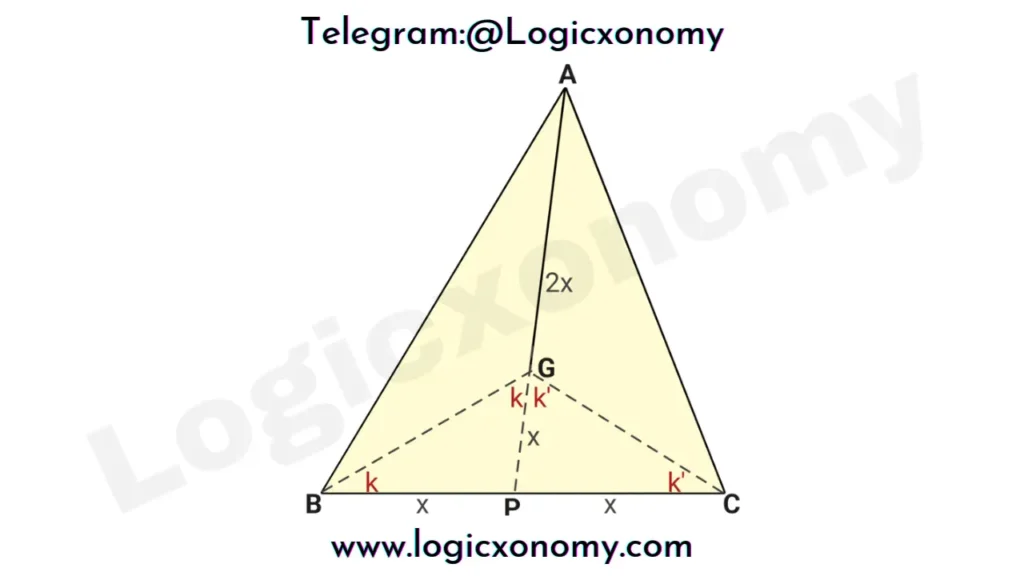
Here, ∆BPG (BP=PG) & ∆CPG (PC=PG) are the Isosceles triangles.
In ∆BGC, the sum of all internal angles =180°
∠CBG+∠BGC+∠GCB=180°
2(k+k’)=180°
k+k’=180°
∠BGC=90°

Coordinates of the Centroid of the triangle
Find the coordinates of the Centroid of the triangle if the coordinates of its vertices are given:
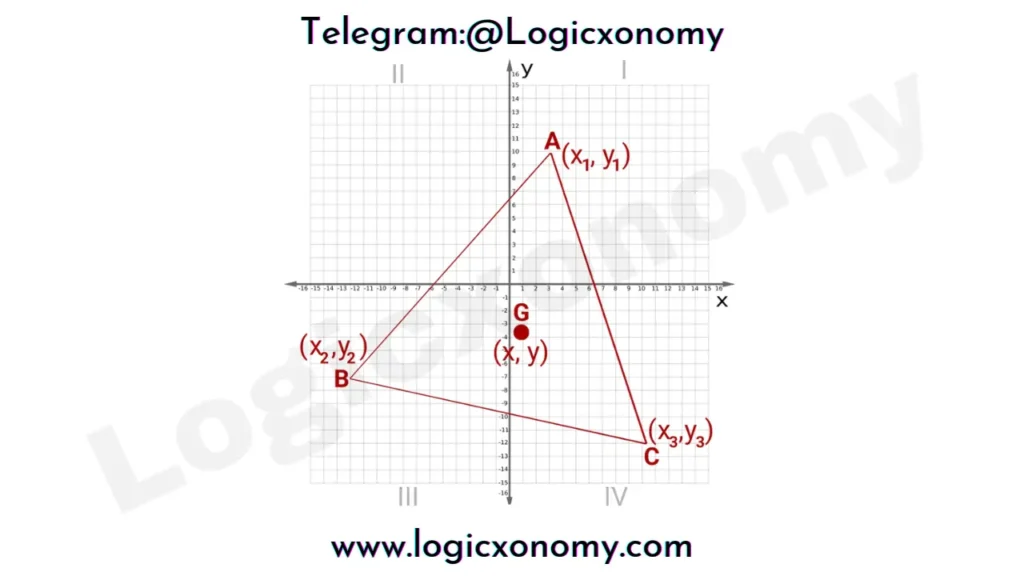
Coordinates of Centroid G=(x,y)
(x,y)=(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})
Stewart’s Theorem
To find the relation between the Cevian and the sides of a triangle, Stewart’s Theorem is used.
Let, In △ABC the lengths of the sides: BC=a, CA=b, and AB=c. Here we have to find the length of the Cevian AD.
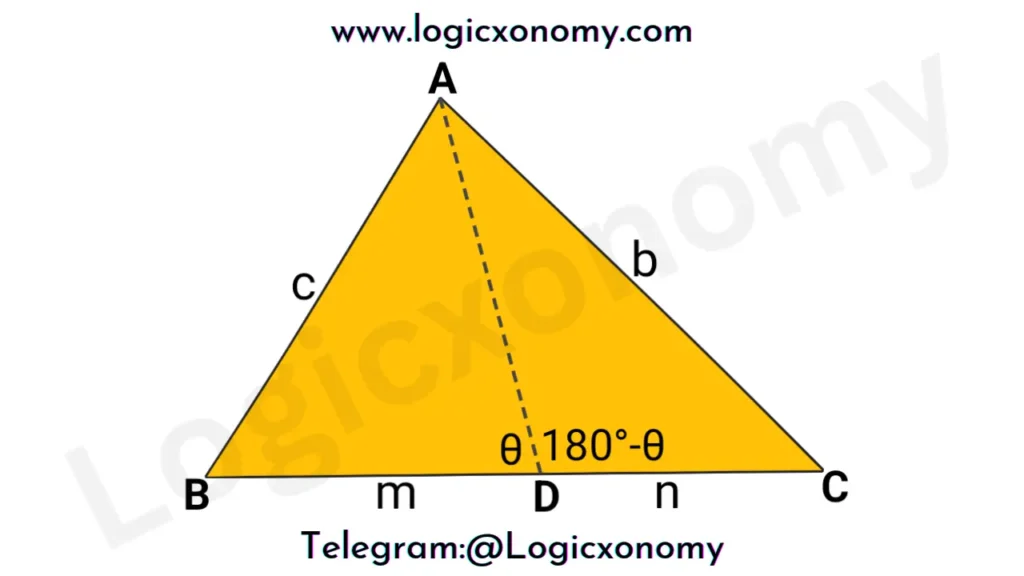
Let ∠ADB=θ then ∠ADC=180°-θ (Linear Pair)
Here BD=m, DC=n, and BC=a
Let AD=d
In △ABD, Use Cosine Formula
c2=m2+d2-2md×Cos(θ) ……….(i)
In △ADC, Use Cosine Formula
b2=n2+d2-2nd×Cos(180°-θ)
b2=n2+d2+2nd×Cos(θ) ……….(ii)
Note: Cos(180°-θ)= -Cos(θ)
Now we have to eliminate the Cosine term from the equations. So multiply equation (i) by n and equation (ii) by m, and after that add both equations.
n.c2=n.m2+n.d2-2mnd×Cos(θ)
m.b2=m.n2+m.d2+2mnd×Cos(θ)
After addition:
m.b2+n.c2=m.n.(m+n)+d2.(m+n)
m.b2+n.c2=(m+n)(d2+m.n)
m.b2+n.c2=a.(d2+m.n) ………(iii)
This equation (iii) is known as Stewart’s Theorem.
In case m=n or AD is the Median of the triangle ABC.
m.b2+n.c2=(m+n)(d2+m.n)
Put n=m
m.(b2+c2)=2m.(d2+m2)
(b2+c2)=2.(d2+m2) ………(iv)
Here m=a/2
This equation (iii) is known as Apollonius’s Theorem. (Centroid of the triangle)
The Length of the Median (Apollonius’s Theorem)
Let, the length of the median AP=d, BC=a, and BP=PC=m (BC=2m)
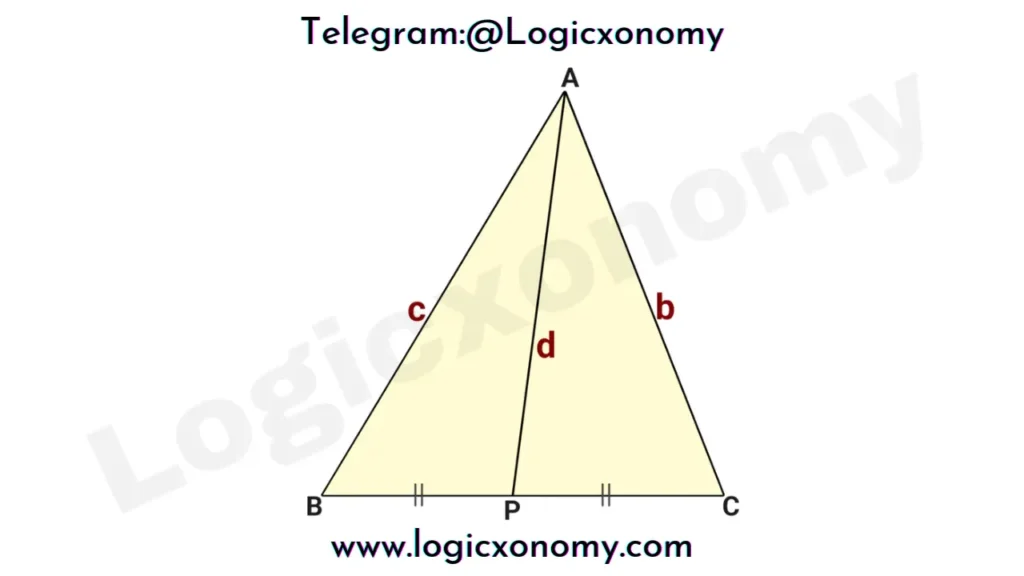
b²+c²=2(m²+d²)
Put m=BC/2=a/2
b²+c²=1/2*(a²+4d²)
The sum of the squares of the lengths of medians

Apply Apollonius Theorem:
AB²+AC²=1/2*(BC²+4AP²)
AC²+BC²=1/2*(AB²+4CR²)
BC²+AB²=1/2*(AC²+4BQ²)
Add all equations:
2(AB²+BC²+CA²)=1/2*[(AB²+BC²+CA²)+4(AP²+BQ²+CR²)]
3/2*(AB²+BC²+CA²)=2(AP²+BQ²+CR²)
(AB²+BC²+CA²)=4/3*(AP²+BQ²+CR²)
Triangle, made by joining the midpoints of the sides
In the given figure:
RQ∥BC & RQ=½*BC
PQ∥AB & PQ=½*AB
PR∥AC & PR=½*AC
The area of ∆PQR=1/4×area of ∆ABC
Note: The centroid of an equilateral triangle also works as its incenter, circumcenter, and orthocenter. In other words, all are the same.
Difference between the Centroid of the triangle and its Circumcenter
| The centroid of the Triangle | The Circumcenter |
| The Centroid of the triangle is the intersection point of the medians of the triangle. | The circumcenter is the intersection point of the perpendicular bisectors of the sides of a triangle. |
| A Median is a Cevian, a line that intersects both a triangle’s vertex and the side opposite to it. | The perpendicular bisector of the side of a triangle does not necessarily pass through the vertex of the triangle or it is not a Cevian. |
| Only in the case of an Equilateral Triangle, the centroid of the triangle and the circumcenter are the same, in other cases, the centroid has different distances from different vertices. | The circumcenter is always equidistant from all the vertices of the triangle. |
| The Centroid of the triangle is always located inside the triangle. | The Circumcenter can be located inside, on the sides, on the vertex, and even outside the triangle. |
| The centroid is the center of gravity of the triangle. | The circumcenter is the center of the circumscribed circle of the triangle. |
Que 1: In the given figure, E is the centroid of the triangle and BCDE is a Parallelogram then find the coordinates of the point ‘D’.
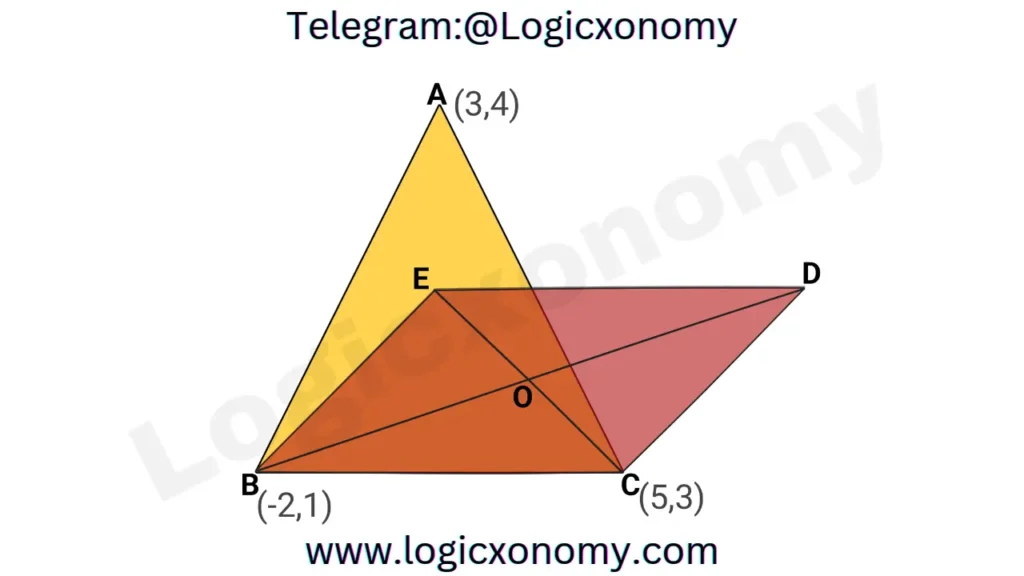
Solution: The coordinates of Centroid (E)= (\frac{3-2+5}{3}, \frac{4+1+3}{3}) =(2, 8/3)
Let the Coordiantes of point D= (a,b)
Use Formula: The coordinates of mid-point between points M(x1,y1) and N(x2,y2)= (\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})
Since, O is the mid-point of BD and EC.
So, The coordinates of the Mid-point of BD= The coordinates of the Mid-point of EC
(\frac{5+2}{2}, \frac{8/3+3}{2})=(\frac{-2+a}{2}, \frac{1+b}{2}).
\frac{-2+a}{2}=\frac{7}{2}.
a=9 ………..(i)
\frac{1+b}{2}=\frac{17/3}{2}.
b=14/3 …………(ii)
The coordinates of Point D= (9, 14/3)
Que 2: Find the coordinates of the centroid of a triangle whose sides are: 12x2 -20xy+ 7y2=0 and 2x-3y+4=0.
Solution: 12x2 -20xy+ 7y2=0, represents a pair of straight lines so first disassociate those two equations.
12x2 -6xy -14xy+ 7y2=0
6x(2x-y) -7y(2x-y)=0
(6x-7y)(2x-y)=0
Now, 6x-7y=0 ……….. Side AB
2x-y=0 ………… Side BC
2x-3y= -4 ………. Side CA
Now, We have to find the coordinates of the vertices of △ABC by taking pair of straight lines and solving them by elimination method.
To find the coordinates of vertex A, we have to solve the equations of lines AB and AC.
6x- 7y=0 ……(i)
(2x- 3y= -4)×3 =6x -9y= -12 ……(ii)
Equation (i)-(ii): 2y=12
y=6
Put this value of y in equation (i): x=7
So, the coordinates of A=(7,6)
Similarly, the Coordinates of B=(0,0)
The coordinates of C=(1,2)
Now, the Coordinates of Centroid= (\frac{7+0+1}{3}, \frac{6+0+2}{3})= (\frac{8}{3}, \frac{8}{3})
Pedal Triangle and Orthic Triangle Concepts: Click Here
Frequently Asked Questions (FAQ):
Can a centroid be outside a triangle?
No, it’s not possible because medians, can’t be drawn outside the triangle so there is no chance of the presence of their intersection point outside the triangle.
What are the properties of a Centroid?
The centroid is the intersection point of the medians of the triangle and its distance from any vertex is always double the distance of its distance from the midpoint of the side, opposite to the respective vertex.
Why is centroid denoted by G?
The centroid represents the center of gravity of the triangle. The Center of gravity is a point in a body of matter where the body’s total weight is thought to be concentrated.
What is the difference between the center of Gravity and the centroid?
In the case of Homogeneous distribution (constant density) of mass across the body, both are the same but for non-uniform distribution, both are different.
What are the types of centers in a triangle?
There are 5 types of centers considered in a triangle:
1. Incenter: Intersection point of the Angle bisectors of the triangle.
2. Circumcenter: Intersection point of the perpendicular bisectors of the sides.
3. Orthocenter: Intersection point of all the Altitudes.
4. Centroid: Intersection point of all the medians.
5. Excenter: Intersection point of the two external angle bisectors and the remaining internal angle.How do construct the centroid of a triangle?
Draw any two medians of the triangle, their intersection point is known as the centroid of the triangle.
Multiple Choice Questions (Quiz)
10 questions with solutions, based on the concepts of the Centroid of the Triangle.

