Fast multiplication tricks with zero possibility of error always give you an advantage in competitive examinations and to fulfill this purpose here we would learn about some unique Mental math tricks and tips.
Use of Percentage in Fast Multiplication
A percentage is a number or ratio expressed as a fraction of 100, denoted using the % sign.
Example: 45%=45/100=0.45
For quick multiplication, the concept of percentage is very useful. Here we would study its application in common calculations.
Fraction Values of Percentage (Multiplication Tricks)
Suppose we have to find the value of 25% of 324.
Here 25%=25/100=1/4 (1/4 is the fraction value of 25%)
So, the required answer=1/4 × 324=81
It means that to find 25% of any value, it should be divided by 4 (multiplied by 1/4)
In other words, we can say 1/4 is the fraction value of 25%
1/4×100%=25%
| Fractions | % (Mixed Fraction) | % (Simplified) |
| \frac{1}{2} | 50% | 50 % |
| \frac{1}{3} | 33\frac{1}{3}% | 33.33 % |
| \frac{1}{4} | 25% | 25 % |
| \frac{1}{5} | 20% | 20 % |
| \frac{1}{6} | 16\frac{2}{3}% | 16.67 % |
| \frac{1}{7} | 14\frac{2}{7}% | 14.28 % |
| \frac{1}{8} | 12\frac{1}{2}% | 12.5 % |
| \frac{1}{9} | 11\frac{1}{9}% | 11.11 % |
| \frac{1}{10} | 10% | 10 % |
| \frac{1}{11} | 9\frac{1}{11}% | 9.09 % |
| \frac{1}{12} | 8\frac{1}{3}% | 8.33 % |
| \frac{1}{13} | 7\frac{9}{13}% | 7.69 % |
| \frac{1}{14} | 7\frac{1}{7}% | 7.14 % |
| \frac{1}{15} | 6\frac{2}{3}% | 6.67 % |
| \frac{1}{16} | 6\frac{1}{4}% | 6.25 % |
| \frac{1}{17} | 5\frac{15}{17}% | 5.88 % |
| \frac{1}{18} | 5\frac{5}{9}% | 5.55 % |
| \frac{1}{19} | 5\frac{5}{19}% | 5.26 % |
| \frac{1}{20} | 5% | 5 % |
| \frac{1}{21} | 4\frac{16}{21}% | 4.76 % |
| \frac{1}{22} | 4\frac{6}{11}% | 4.54 % |
| \frac{1}{23} | 4\frac{8}{23}% | 4.35 % |
| \frac{1}{24} | 4\frac{1}{6}% | 4.16 % |
| \frac{1}{25} | 4% | 4 % |
| \frac{1}{26} | 3\frac{11}{13}% | 3.84 % |
| \frac{1}{27} | 3\frac{19}{27}% | 3.70 % |
| \frac{1}{28} | 3\frac{4}{7}% | 3.57 % |
| \frac{1}{29} | 3\frac{13}{29}% | 3.45 % |
| \frac{1}{30} | 3\frac{1}{3}% | 3.33 % |
Other important fractions:
1/8=12.5%, 2/8=25%, 3/8=37.5%, 4/8=50%
5/8=62.5%, 6/8=75%, 7/8=87.5%, 8/8=100%
1/6=16.67% then 83.33%=100%-16.67%=1-1/6=5/6
Que 1: Find 178% of 742
Solution:
| Method:1 178% of 742 =(200% – 20% – 2%)×742 =(2 - \frac{2}{10} - \frac{2}{100})×742 =1484 – 148.4 – 14.84 =1484 – 163.24 =1320.76 | Method:2 742% of 178 =(700% + 50% – 10% + 2%)×178 =(7 - \frac{1}{2} - \frac{1}{10})×178 =1246 + 89 – 17.8 +2×1.78 =1246 + 89 – 17.8 + 3.56 =1320.76 |
Que 2: Find the value of 1667×1428×3738
(a) 7354151788
(b)8543714218
(c)8898219288
(d)9163818218
Solution:
1667=16.67×100=16.67% ×100×100=1/6×10000
1428=14.28×100=14.28% ×100×100=1/7×10000
=1/6×1/7×3738×100000000
=89×100000000
=8900000000 (Approximately)
So, Option (C) is correct.

Que 3: Find the value of 57×78
Solution:
=57%×100×78
=(50%+5%+2%)×78×100
=(1/2+1/20+2/100)×78×100
=(39+3.9+1.56)×100
=44.46×100
=4446
Product of numbers whose sum of unit digits is equal to 10
Multiplication Tricks for the product of two numbers in a special case.
Conditions (Multiplication Tricks):
- Only the unit digits of the two numbers should be different and the sum of the unit digits should be equal to 10.
- Unit digits could be the same also, in the case of 5 and 5 because 5+5=10.
Que 1: Find the value of 36×34.
Step 1: Product of unit digits= 6×4=24 (It should be of 2 digits)
Step 2: n, a number made by the remaining digits
Here n=3
n×(n+1)=3×4=12
Required product of the numbers=1224
Que 2: Find the value of 151×159.
Step 1: Product of unit digits= 1×9=09 (It should be of 2 digits)
Step 2: n, a number made by the remaining digits
Here n=15
n×(n+1)=15×16=(30/2)×16=240
Required product of the numbers=24009
Que 3: Find the value of 145².
145²=145×145
Step 1: 5²=25
Step 2: 14×15=14×(30/2)=210
Required product of the numbers=21025
The product of mixed fractions whose sum of fractional parts is equal to 1
Conditions (Multiplication Tricks):
- The sum of fractional parts =1
- The whole numbers should be the same.
Que 1: Find the value of 17\frac{2}{7}×17\frac{5}{7}?
Step 1: Product of fractional parts=
\frac{2}{7}×\frac{5}{7}=\frac{10}{49}
Step 2: n, whole number
n×(n+1)=17×18=17×(17+1)=17²+17=289+17=306
Required product =306\frac{10}{49}
Que 2: Find the value of 7\frac{5}{9}×7\frac{4}{9}?
Step 1: Product of fractional parts=
\frac{5}{9}×\frac{4}{9}=\frac{20}{81}
Step 2: n, whole number
n×(n+1)=7×8=56
Required product =56\frac{20}{81}
The square of any number (Multiplication Tricks)
Here we would use a very common formula of the square but in a different way
(a+b)²=a²+2ab+b²
Que 1: Find the value of 43².
Step 1: Break the number into two parts (a & b)
where ‘b’ is the unit digit and ‘a’ is the remaining part.
Step 2: a² / 2ab / b²
=4² / 2×4×3 / 3²
=16 / 24 / 9
=16+2 / 4 / 9
=18 / 4 / 9
=1849
The required result=1849
Que 2: Find the value of 127².
Step 1: Break the number into two parts (a & b)
where ‘b’ is the unit digit and ‘a’ is the remaining part.
Step 2: a² / 2ab / b²
=12² / 2×12×7 / 7²
=144 / 168 / 49
=144 / 168+4=172 / 9
=144 / 172 / 9
=144+17 / 2 / 9
=161 / 2 / 9
The required result=16129
Multiplication by 11 (Multiplication Tricks)
Que 1: Find the value of 41573×11.
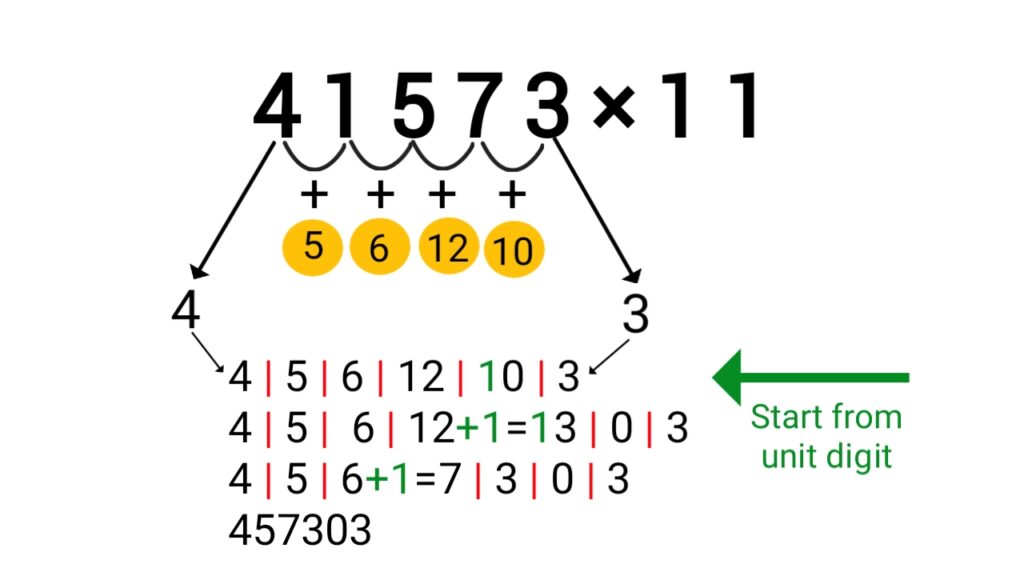
Que 2: Find the value of 47×11.
= 4 / 4+7=11 / 7
=4+1=5 / 1 / 7
=517
Magical Pyramids (Multiplication Tricks)
- Series of 1 (Multiplication Tricks):
11×11=121
111×111=12321
1111×1111=1234321
11111×11111=123454321
111111×111111=12345654321
…..and so on
- Series of 3 (Multiplication Tricks):
3²=09
33²=1089
333²=110889
3333²=11108889
33333²=1111088889
333333²=111110888889
…..and so on
- Series of 6 (Multiplication Tricks):
6²=36
66²=4356
666²=443556
6666²=44435556
66666²=4444355556
666666²=444443555556
…..and so on
- Series of 9 (Multiplication Tricks):
9²=81
99²=9801
999²=998001
9999²=99980001
99999²=9999800001
999999²=999998000001
…..and so on
Que: Find the value of 44444×55555.
Solution:
=11111×4×11111×5
=11111²×20
=123454321×20
=2469086420
Difference between Place Value and Face Value
Place Value: It gives the value of a digit based on its position in a number. It changes according to the place of the digit.
Face Value: The actual value of the digit.
Example: Let’s take the number 24578
| Position | Place Value | Face Value |
| Unit digit Tens digit Hundreds digit Thousands digit Ten-Thousands digit | 8×1=8 7×10=70 5×100=500 4×1000=4000 2×10000=20000 | 8 7 5 4 2 |
Multiplying the numbers close to 100
Case 1: Both the numbers are below 100
Example (1): 89×97 (Multiplication Tricks)
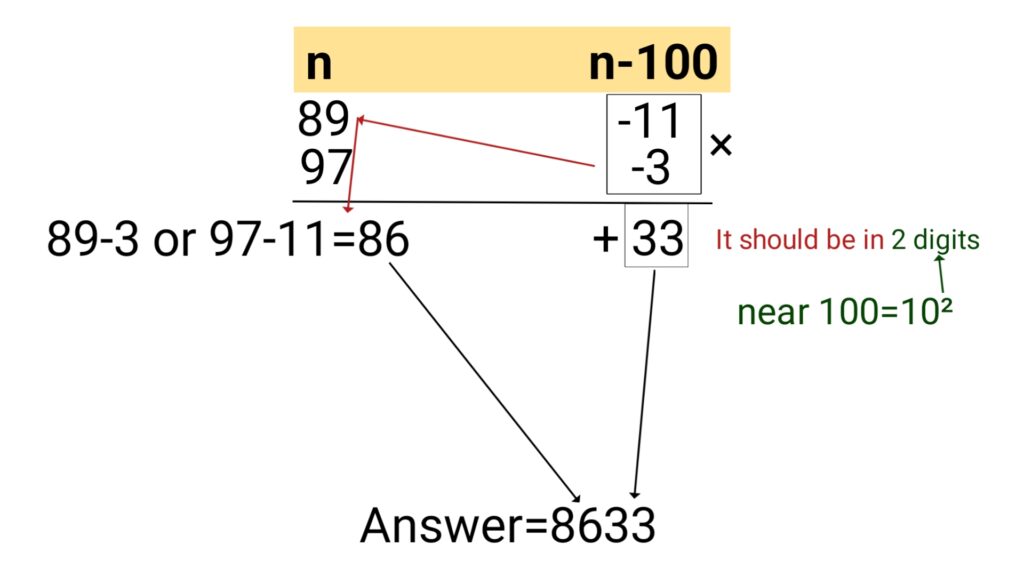
Example (2): 97×98
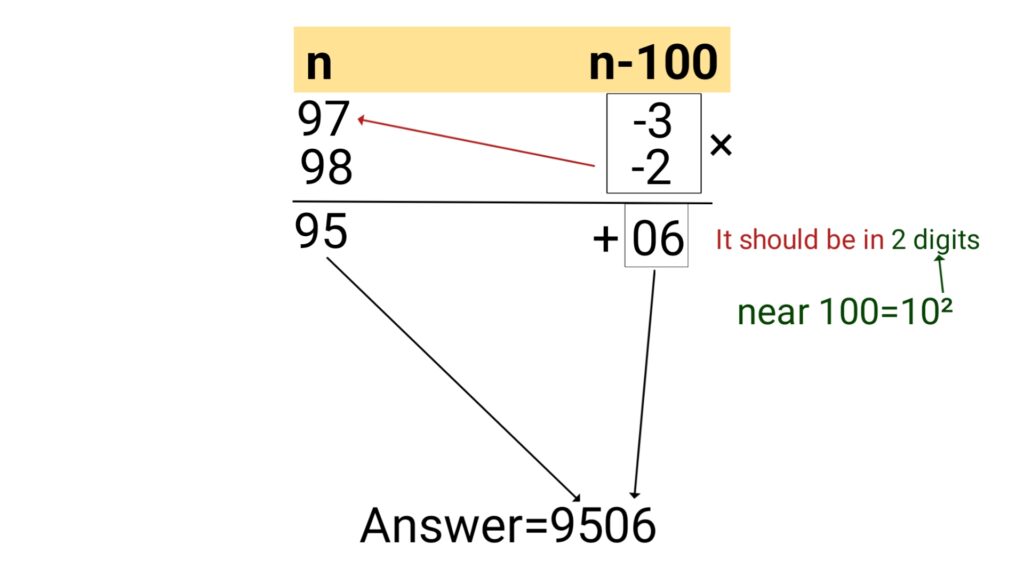
Example (3): 88×85
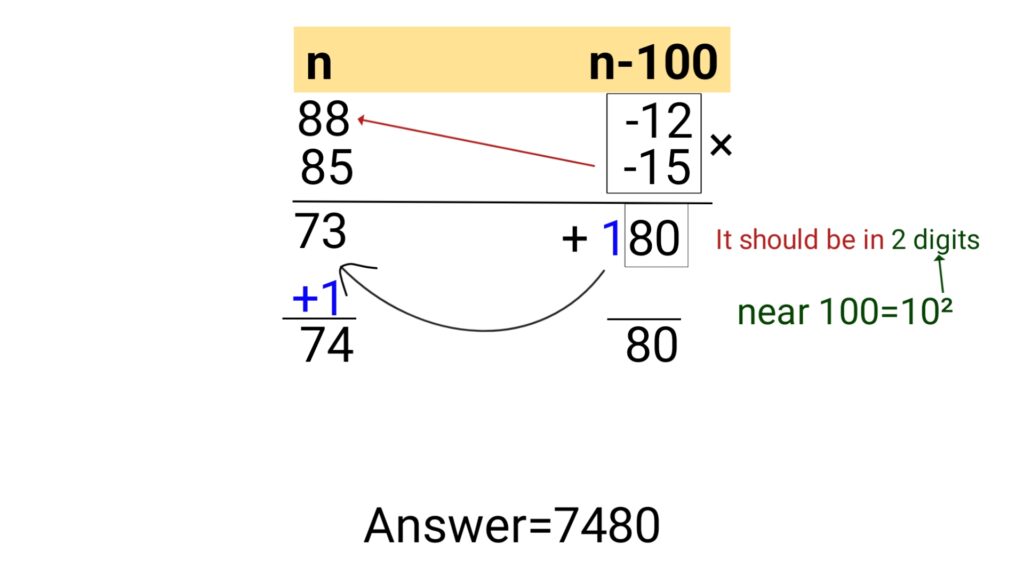
Case 2: Both the numbers are above 100
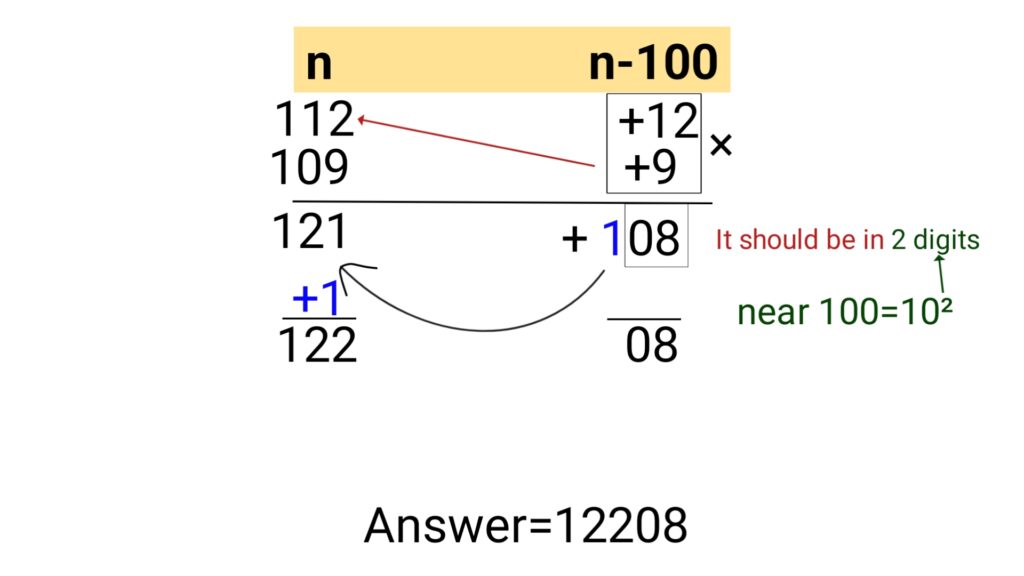
Example (1): 112×109
Case 3: One number is greater and another is lesser than 100
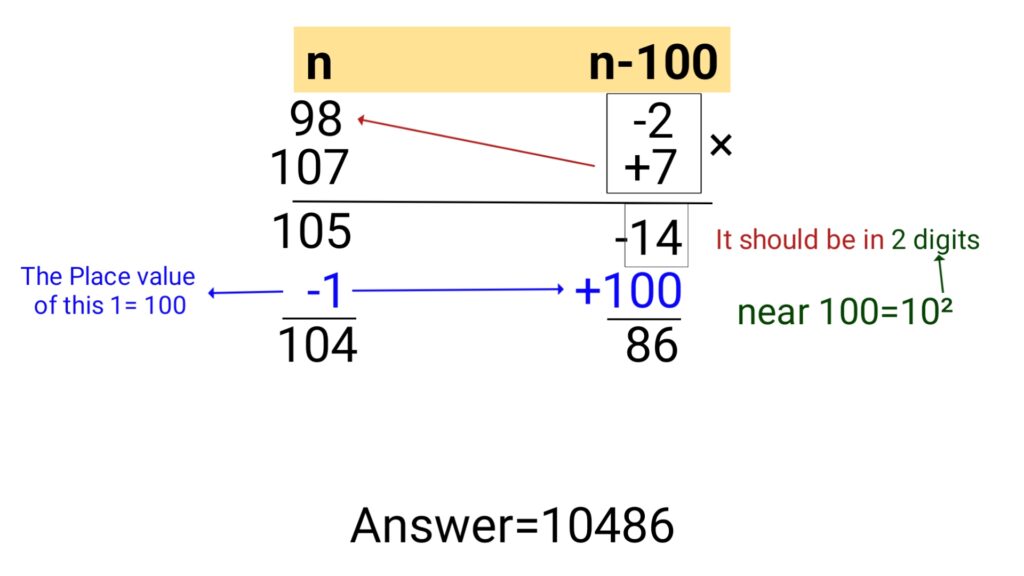
Example (1): 98×107
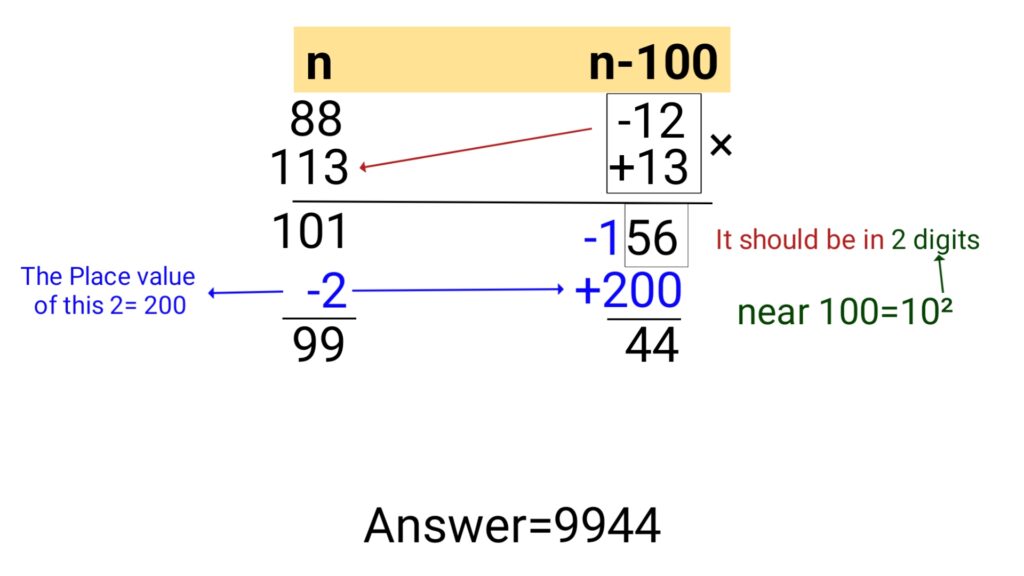
Example (2): 88×113
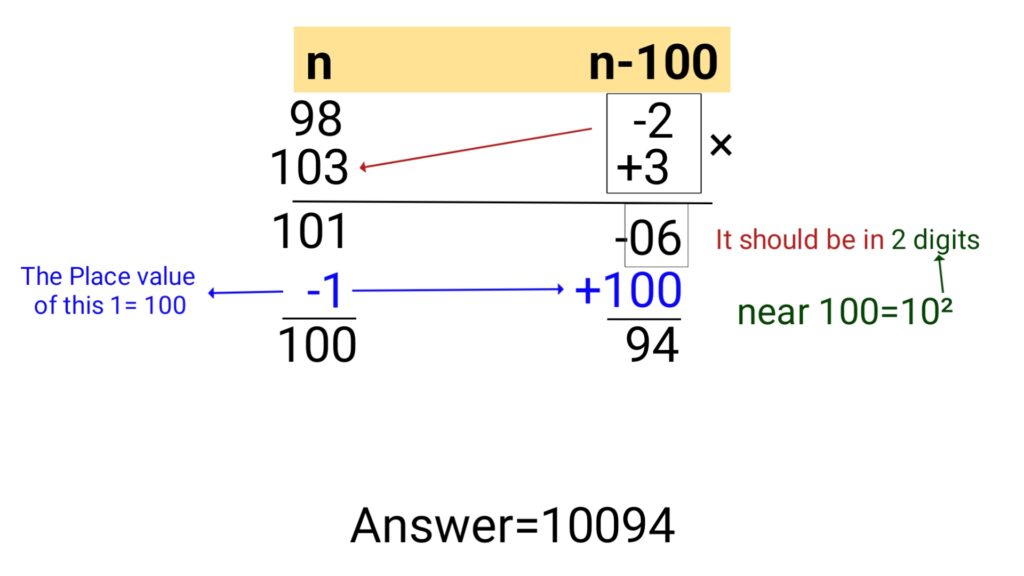
Example (3): 98×103
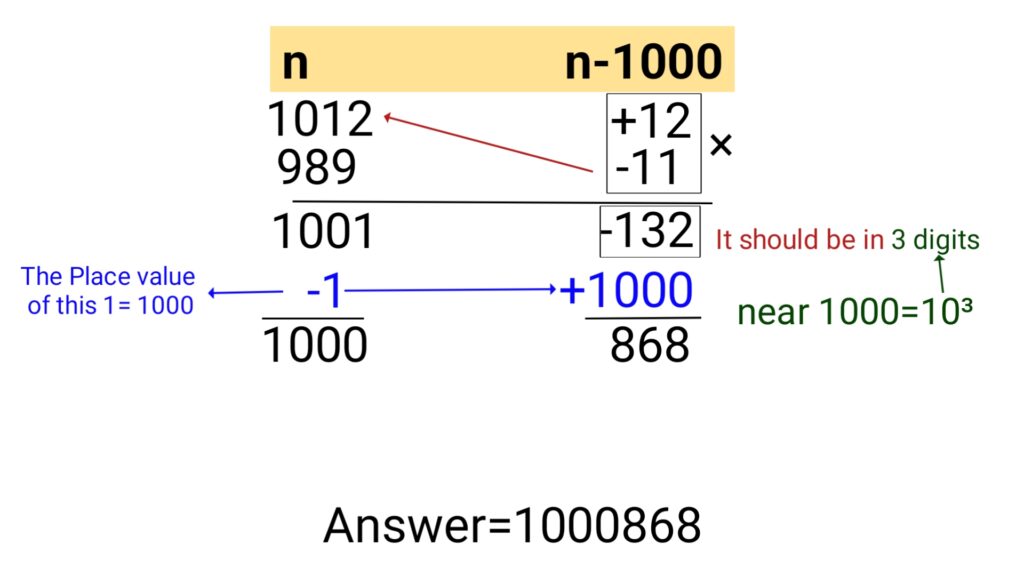
Multiplying the numbers close to 1000
The method is the same as given above, with a very slight difference
Example: 1012×989
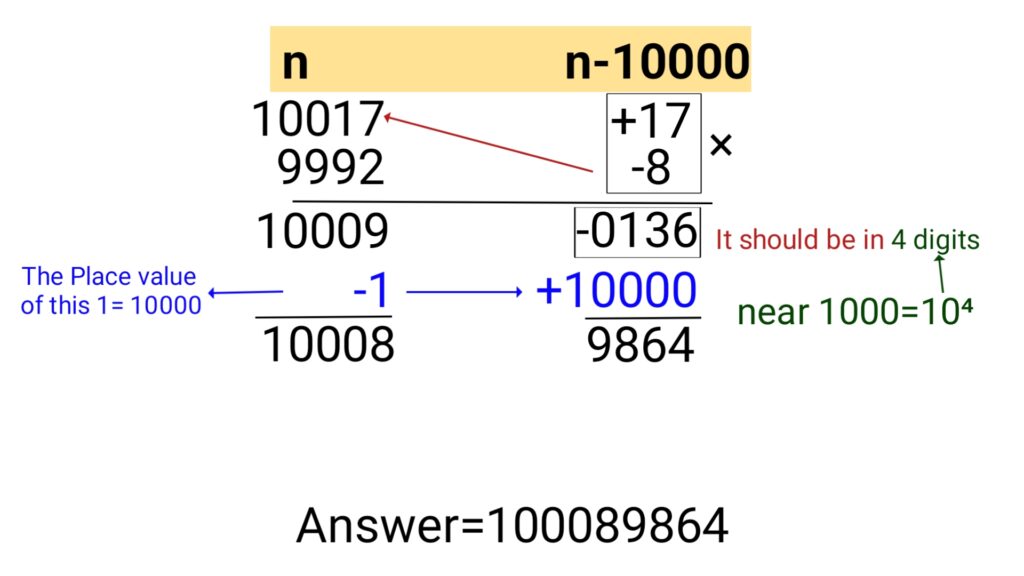
Multiplying the numbers close to 10000
Example: 10017×9992
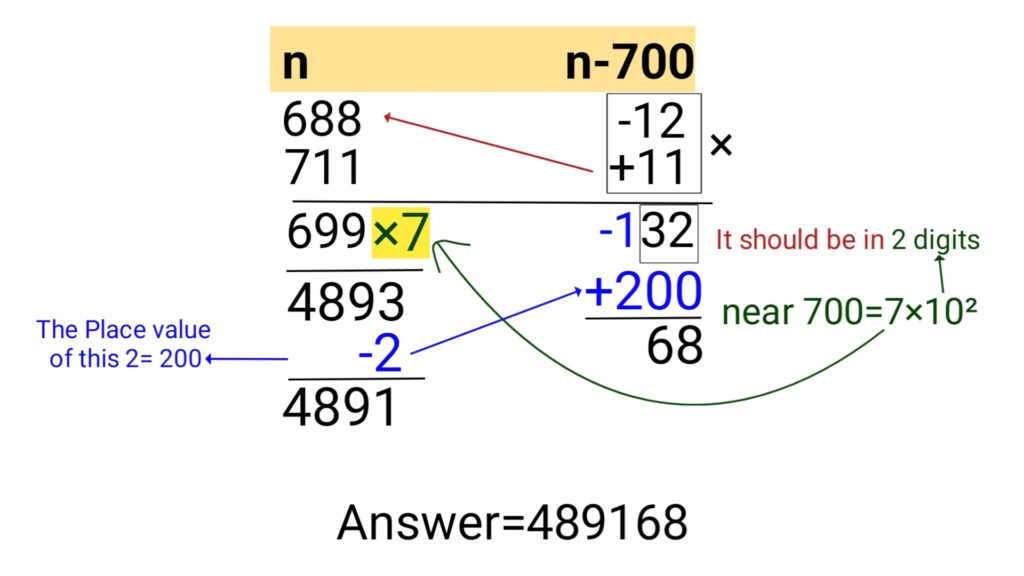
Multiplying the numbers close to 700
700=7×10²
Example: 688×711
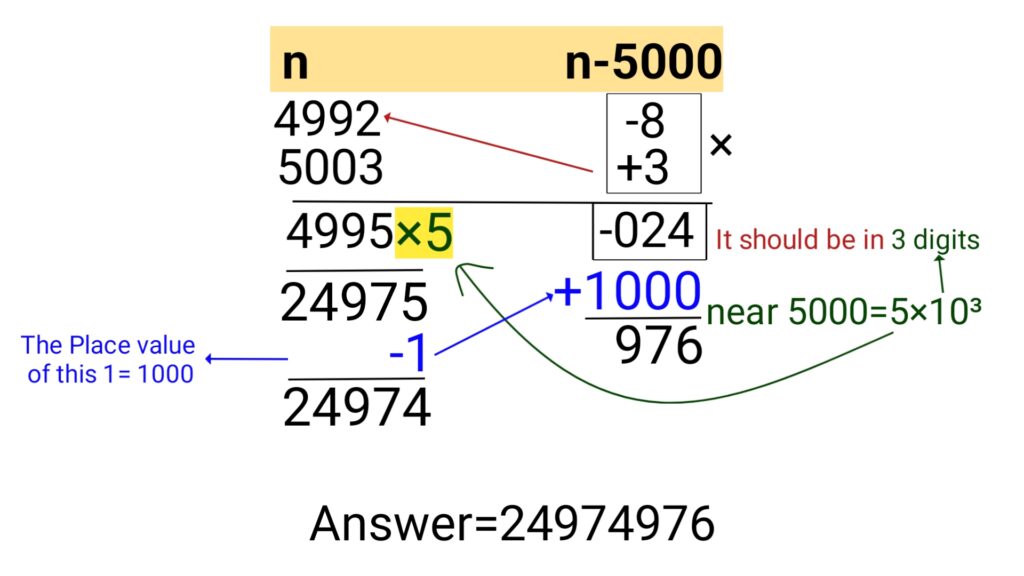
Multiplying the numbers close to 5000
Example: 4992×5003
Note: Division is easy in comparison to multiplication. So, avoid multiplying with more than one digit to reduce the calculation error and time.
×5=×\frac{10}{2}
×25=×\frac{100}{4}
×125=×\frac{1000}{8}
×625=×\frac{10000}{16}
×75=×\frac{300}{4}
×15=×\frac{30}{2}
….and so on
Surds and Indices concepts and tricks: Click Here
Frequently Asked Questions
Difference between factors and multiples.
Factors: The factor of any number can completely divide that number.
Example: Factors of 12 are 1,2,3,4,6,12.
Multiples: A multiple can be obtained by multiplying any number with an integer.
Example: 12× -1= -12, 12× 0= 0, 12× 1= 12, 12× 5= 60 ,etc.What is Prime Factorization?
Every number can be expressed in the form of a product of its Prime factors. This way of expression is known as Prime Factorization.
Example: 12=2²×3, 100=2²×5², 3780=2²×3³×5×7, etc.What are the rules of multiplication?
Any number multiplied with zero results in always being zero.
The result of the multiplication of two numbers with different signs is always negative.
Negative × Negative= Positive
Positive × Positive= Positive
Negative × Positive= NegativeWhat is the relationship between multiplication and addition?
Multiplication is the quick method of repeated addition of any number.
Example: 4×5=20
The sum of fours, five times: 4×5=4+4+4+4+4
The sum of fives, four times: 4×5=5+5+5+5Who invented Multiplication?
Multiplication is one of the four elementary arithmetic operations with addition, subtraction, and division.
The ancient Babylonians are considered the inventors of multiplication tables, dating back to 4000 years.
Quick Multiplication (Quiz)
12 questions with solutions, based on the concept of quick multiplication.

