Simplification and approximation are crucial concepts in time-bound competitive examinations such as aptitude tests, bank exams, and various other competitive and entrance exams. These techniques allow aspirants to solve complex problems more quickly and efficiently within the allotted time frame, making it easier for them to score higher marks.
Moreover, simplification and approximation techniques are not only useful in mathematics but also in other subjects such as physics, chemistry, and economics. Therefore, mastering these techniques can significantly improve a candidate’s chances of success in examinations.
Here we are going to discuss some of the key concepts which can help us to solve complex mathematical calculations without pen and paper like unit digits, the last two or three digits, the divisibility rule, the Digital Sum method, mixed fractions, VBODMAS, and percentages. (Simplification and approximation)
Find the Remainder
Find the remainder when 112×271×17+1008×25-720+54 is divided by 7.
⇒(112×271×17+1008×25-720+54) mod 7
Note: ‘mod’ is the modulo operator that yields the remainder of an integer division.
Method: Replace each number with its respective remainder (remaining after dividing the respective number by 7)
If the division sign is present in the expression, first solve that part of the expression, then apply this concept. (Simplification and approximation)
⇒(0×5×3+0×4-6+5) mod 7
⇒(0+0-6+5) mod 7
⇒ -1
Make this negative remainder positive by adding 7 (Divisor) to it.
-1+7=6
The required remainder= 6
Que: (124+7205×412×672- 298×27+54) mod 8
Solution: (4+5×4×0- 2×3+6) mod 8
=(4+0-6+6) mod 8
=4
Important Remainder Problems: Click Here
Concept of Negative Remainder
In a division process, the dividend is the number being divided, the divisor is the number by which it is being divided, the quotient is the result of the division, and the remainder is the amount left over after the division is complete. The remainder is always smaller than the divisor.
Dividend= Divisor×Quotient+Remainder

We can turn a negative remainder into a positive one by adding it to the divisor.
Note: The sign of the remainder is always the same as the sign of the dividend.
Here are some special cases of the division process:
Case 1: When the divisor is Negative
Que: Find the remainder when 23 is divided by -4
Here the sign of the remainder will be positive
Dividend= Divisor×Quotient+Remainder
23=-4×(-5)+ Remainder
Remainder=3
Case 2: When the dividend is Negative
Que: Find the remainder when -23 is divided by 4
Here the sign of the remainder will be negative (Simplification and approximation)
Dividend= Divisor×Quotient+Remainder
-23=4×(-5)+ Remainder
Remainder= -3
Case 3: When both the dividend and the divisor are negative
Que: Find the remainder when -23 is divided by -4
Here the sign of the remainder will be negative (Simplification and approximation)
Dividend= Divisor×Quotient+Remainder
-23=-4×(5)+ Remainder
Remainder= -3
Case 4: When both the dividend and the divisor are positive
Que: Find the remainder when 23 is divided by 4
Here the sign of the remainder will be positive
Dividend= Divisor×Quotient+Remainder
23=4×(5)+ Remainder
Remainder= 3
Divisibility Rules
(A) Divisibility Rule of 2: The unit digit should be 0,2,4,6 or 8.
(B) Divisibility Rule of 3: The sum of the digits of the number must be divisible by 3. If the sum of the digits is not divisible by 3, then the remainder when the sum of the digits is divided by 3 is the same as the remainder when the given number is divided by 3.
Concept: Let PQRS be a four-digit number (Simplification and approximation)
PQRS= 1000×P+100×Q+10×R+S
(1000×P+100×Q+10×R+S) Mod 3
⇒(1×P+1×Q+1×R+S) mod 3
⇒(P+Q+R+S) mod 3
⇒(Digit Sum) mod 3
Que: Find the remainder when 567432 is divided by 3.
Method 1: (5+6+7+4+3+2) mod 3= 0
It means that the given number is divisible by 3.
Method 2: (Simplification and approximation)
First, remove all digits divisible by 3⇒ 5742
Eliminate all pairs of numbers whose sum is divisible by 3⇒ 57 42
Remainder=0
(C) Divisibility Rule of 4: To find the remainder after dividing a number by 4, divide only its last two digits by 4 and find the remainder. If it is zero then the number is divisible by 4.
Concept: Let, ABCDEFG is a 7-digit number then
ABCDEFG= ABCDE×100+FG
Here, the yellow part is already divisible by 4 because 100 is divisible by 4.
Que: Find the remainder when 567437 is divided by 4.
Solution: 37 mod 4= 1
(D) Divisibility Rule of 5: The unit digit must be 0 or 5.
If the given number is N (Simplification and approximation)
N mod 5= (Unit Digit) mod 5
(E) Divisibility Rule of 6: The number must be divisible by both 2 and 3. (Simplification and approximation)
(F) Divisibility Rule of 7,11 & 13: The method to find whether a given number is divisible by 7, 11, and 13 is the same.
Concept: 1001=7×11×13
⇒ 1001 mod 7
⇒ (1000+1) mod 7
⇒ (-1+1) mod 7
The sequence from the right-hand side is + ve and then – ve (Simplification and approximation)
Que 1: Find the remainder when 4576218359 is divided by 7.
Step 1: Divide the given number into pairs of 3 from the right and keep the arithmetic operators + and – in order from the right.
-004+576-218+359
Step 2: (576+359)-(4+218)= 935-222= 713
Step 3: 713 mod 7= 6
713 mod 11=9
713 mod 13=11
Que 2: Find the remainder when 23457621835927189342 is divided by 7.
Solution: 23-457+621-835+927-189+342
⇒ (23+621+927+342)-(457+835+189)
⇒ 1913- 1481
⇒ 432
432 mod 7= 5
432 mod 11= 3
432 mod 13= 3
(G) Divisibility Rule of 8: To find the remainder after dividing a number by 8, divide only its last three digits by 8 and find the remainder. If it is zero then the number is divisible by 8. (Simplification and approximation)
Concept: Let, ABCDEFG is a 7-digit number then
ABCDEFG= ABCD×1000+EFG
Here, the yellow part is already divisible by 8 because 1000 is divisible by 8.
Que: Find the remainder when 567437 is divided by 8.
Solution: 437 mod 8= 5
(H) Divisibility Rule of 9: The sum of the digits of the number must be divisible by 9. If the sum of the digits is not divisible by 9, then the remainder when the sum of the digits is divided by 9 is the same as the remainder when the given number is divided by 9.
Concept: Let PQRS be a four-digit number (Simplification and approximation)
PQRS= 1000×P+100×Q+10×R+S
(1000×P+100×Q+10×R+S) Mod 9
⇒(1×P+1×Q+1×R+S) mod 9
⇒(P+Q+R+S) mod 9
⇒(Digit Sum) mod 9
Que: Find the remainder when 567432 is divided by 9.
Solution: First, eliminate all pairs of numbers whose sum is divisible by 9⇒ 54 63 72
Remainder=0
(I) Divisibility Rule of 11: Find the remainder when 173567432 is divided by 11.
Concept: 11=1×10+1 (Simplification and approximation)
(1×10+1) mod 11= (-1+1)
⇒ 173567432 mod 11
⇒ (+1-7+3-5+6-7+4-3+2) mod 11
⇒ (1+3+6+4+2)-(7+5+7+3) mod 11
⇒ (16-22) mod 11
⇒ -6
⇒ -6+11
⇒ 5
(J) Divisibility Rule of 3 and 37: If N=44444444……..44 is a 367-digit number then find the remainder if N is divided by 3 or 37.
Concept: 111=3×37
It means that if a number is repeated 3k times then it is divisible by 3 and 37. Here k is a whole number.
Total digits= 367
Remove all three-digit pairs
367 mod 3= 1
Now, there is only one 4 left.
4 mod 3= 1
4 mod 37= 4
(K) Divisibility Rule of 3, 7, 11, 13, and 37: If N=44444444……..44 is a 542-digit number then find the remainder if N is divided by 3, 7, 11, 13, or 37.
Concept: 111111=3×7×11×13×37
It means that if a number is repeated 6k times then it is divisible by 3, 7, 11, 13, and 37. Here k is a whole number.
Total digits= 542
Remove all six-digit pairs
542 mod 6= 2
Now, there are only two 4 left.
44 mod 3= 2
44 mod 7= 2
44 mod 11= 0
44 mod 13= 5
44 mod 37= 7
(L) Divisibility Rule of 99: Find the value of 173567432 mod 99
Step 1: Break it into two-digit pairs, starting with the unit digit
1×1006+73×1004+56×1002+74×100+32×1
Step 2: Apply the Modulo operation
⇒ [1×1004+73×1003+56×1002+74×100+32×1] mod 99
⇒ [1×16+73×14+56×12+74×1+32×1] mod 99
⇒ [1+73+56+74+32] mod 99
⇒ [Sum of pairs] mod 99
Note: If the sum of the pairs is greater than 99, then immediately calculate the remainder from 99.
73+56= 129 ⇒ 129 mod 99= 30
30+74= 104 ⇒ 104 mod 99= 5
1+5+32= 38 ⇒ 38 mod 99= 38
Answer= 38
Que: N=123456…. is a 51-digit number then find the remainder when N is divided by 99?
(a) 0
(b) 1
(c) 98
(d) None
Solution: From 1 to 9 total of 9 digits, then pairs of two digits. Let k numbers of two digits be required to complete 51 digits.
9+2k=51
k=21
So the last number= 9+k=30
N=12345……..282930
Apply the divisibility rule of 99:
01+23+45+67+89+(10+11+12+…….+30)
Here the yellow part is in A.P. (Arithmetic Progression)
⇒[(01+89)+(23+67)+45]+{(10+30)/2}×21
⇒[90+90+45]+420
Now, (90+90+45+420) mod 99=(-9-9+45+24)=51
Option(d)
(M) Divisibility Rule of 999: Find the value of 3173567432489723 mod 999
Step 1: Break it into three-digit pairs, starting with the unit digit
3×10005+173×10004+567×10003+432×10002+489×1000+723×1
Step 2: Apply the Modulo operation
⇒ [3×10005+173×10004+567×10003+432×10002+489×1000+723×1] mod 999
⇒ [3×15+173×14+567×13+432×12+489×1+732] mod 999
⇒ [3+173+567+432+489+732] mod 999
⇒ [Sum of pairs] mod 999
Note: If the sum of the pairs is greater than 999, then immediately calculate the remainder from 999.
723+489= 1212 ⇒ 1212 mod 999= 213
213+432+567= 1221 ⇒ 1212 mod 999= 213
213+173+3= 389
Answer= 389

Find the Unit Digits
The unit digit comes at the ones place of any number. For example, in the number 326, the unit digit is 6. The units digit is important because it can help determine various mathematical properties of a number, such as divisibility, remainder, and cyclicity. (Simplification and approximation)
The unit digit is basically the remainder after dividing any number by 10.
Unit Digit= N mod 10
Here N is a number and ‘mod’ is the modulo operator that yields the remainder of an integer division.
Que 1: Find the unit digit of the given expression:112×271×17+1008×25-720+54
Solution: Remove all numbers except unit digits from the given expression (Simplification and approximation)
Note: You can do this if the division operator (÷) is not present.
⇒ 2×1×7+8×5-0+4
⇒ 14+40+4
Again repeat a similar method
⇒ 4+0+4
⇒ 8
Unit Digit= 8
Que 2: Find the unit digit of the given expression:112×271÷17+1008×25-720+54
Solution: Here, the division operator (÷) is present so first, we use the VBODMAS rule
V⇒ Vinculum (The bar x you see on top of the values)
B⇒ Brackets – ( ), { }, [ ]
O⇒ Of
D⇒ Division (÷)
M⇒ Multiplication (×)
A⇒ Addition (+)
S⇒ Subtraction (-)
⇒(112×271÷17)+1008×25-720+54
Solve this yellow part first then use the unit digit method.
⇒(112×271÷17)+1008×25-720+54
Neither 112 nor 271 is completely divisible by 17
112×271= (100+10+2)×271
=27100+2710+542
=30352
Now, 30352÷17= 1785.xxx (Only the whole number required)
⇒1785+1008×25-720+54
⇒5+8×5-0+4
⇒5+40+4
⇒5+0+4
⇒9
Unit Digit= 9
Que 3: Given 467×472×477×482= m2-n then find the value of m-n.
(a) 224491
(b) 224494
(c) 224495
(d) 224499
Solution: The unit digit of LHS= 7×2×7×2= 6
m2 is a perfect square number so its unit digits could be⇒ 1, 4, 9, 6, 5
467×472×477×482+n= m2
| Unit digit of the product | Unit digit of n | Unit digit of m2 | Unit digits of m | Unit digit of m-n |
| 6 | 5 | 1 | 1 or 9 | 1-5=6 or 9-5=4 |
| 8 | 4 | 2 or 8 | 2-8=4 or 8-8=0 | |
| 3 | 9 | 3 or 7 | 3-3=0 or 7-3=4 | |
| 0 | 6 | 4 or 6 | 4-0=4 or 6-0=6 | |
| 9 | 5 | 5 | 5-9=6 |
This means that the only possible unit digits of m-n are 0, 4, and 6.
Option (b) is correct.
The Nth root of any number
Here we will use the formula to find the approximate value of the nth root of a number.
\sqrt[n]{a}=x\pm\frac{y}{n\times x^{n-1}}.
Here y=|xn-a| and the value of y must be as small as possible.
n,x and a are positive integers.
If xn>a then choose the negative sign and in other case choose positive
Que 1: Find the value of \sqrt[4]{513}.
Solution: a=513 and n=4
44=256 and 54=625
Now xn should be nearer to a. So the possible value of x is 5
y=xn-a=625-513=112
Here, xn>a
\sqrt[n]{a}=x-\frac{y}{n\times x^{n-1}}.
Put x=5, y=112, and n=4 in this formula.
\sqrt[4]{513}= 4.776 (Approx)
Actual value up to two decimal places, by using Calculator=4.75
Que 2: Find the value of \sqrt[3]{178}.
Solution: 63=216 and 53=125 (Simplification and approximation)
So the possible value of x is 6
y=xn-a=216-178=38
Here, xn>a
\sqrt[n]{a}=x-\frac{y}{n\times x^{n-1}}.
Put x=6, y=38, and n=3 in this formula.
\sqrt[3]{178}= 5.649 (Approx)
Actual value up to two decimal places, by using Calculator=5.62
Que 3: Find the value of \sqrt[5]{615}.
Solution: 35=243 and 45=1024 (Simplification and approximation)
So the possible value of x is 3
y=a-xn=615-243=372
Here, xn<a
\sqrt[n]{a}=x+\frac{y}{n\times x^{n-1}}.
Put x=3, y=372, and n=5 in this formula.
\sqrt[5]{615}= 3.91 (Approx)
Actual value up to two decimal places, by using Calculator=3.61
Que 4: Find the value of \sqrt[6]{437}.
Solution: 26=64 and 36=729 (Simplification and approximation)
So the possible value of x is 3
y=xn-a=729-437=292
Here, xn>a
\sqrt[n]{a}=x-\frac{y}{n\times x^{n-1}}.
Put x=3, y=292, and n=6 in this formula.
\sqrt[6]{437}= 2.8 (Approx)
Actual value up to two decimal places, by using Calculator=2.75
Que 5: Find the value of \sqrt[6]{1156}.
Solution: 36=729 and 46=4096
So the possible value of x is 3
y=a-xn=1156-729=427
Here, xn<a
\sqrt[n]{a}=x+\frac{y}{n\times x^{n-1}}.
Put x=3, y=427, and n=6 in this formula.
\sqrt[6]{1156}= 3.29 (Approx)
Actual value up to two decimal places, by using Calculator=3.24
Fractions
Competitive exam questions on fractions may cover topics such as continued fractions, comparing fractions, and mixed fractions, testing your mathematical proficiency in these areas. Being familiar with these concepts is crucial for success in such exams.
Continued Fractions
Que 1: Find the value of a-b+c-d+e-f (Simplification and approximation)
\frac{1}{a+\frac{1}{b+\frac{1}{c+\frac{1}{d+\frac{1}{e+\frac{1}{f}}}}}}=\frac{2995}{6573}.
Solution: a= Quotient (6573÷2995)=2, Remainder=583
b= Quotient (2995÷583)=5, Remainder=80
c= Quotient (583÷80)=7, Remainder=23
d= Quotient (80÷23)=3, Remainder=11
e= Quotient (23÷11)=2, Remainder=0
f=11

a-b+c-d+e= 2-5+7-3+2-11= -8
Que 2: Find the value up to two decimal places (Simplification and approximation)
\frac{1}{1+\frac{1}{2-\frac{1}{3+\frac{1}{4-\frac{1}{5+\frac{1}{6}}}}}}+\frac{1}{1-\frac{1}{2+\frac{1}{3-\frac{1}{4+\frac{1}{5-\frac{1}{6}}}}}}
Solution: Here we will solve both fractions separately and then add them

Solution of the first continued fraction




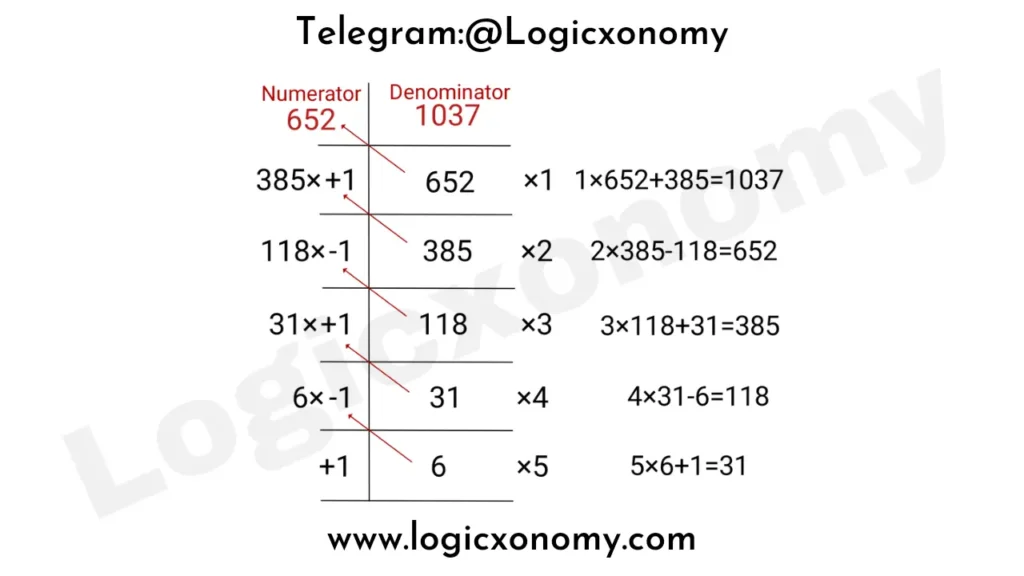
First fraction= \frac{652}{1037} ………..(i)
The solution of the second fraction:

Second fraction= \frac{796}{459} ………..(ii)
Final result= \frac{6.52}{10.37}+\frac{7.96}{4.59}=\frac{6}{10}+\frac{7}{4}=2.35 (approx.)
Que 3:
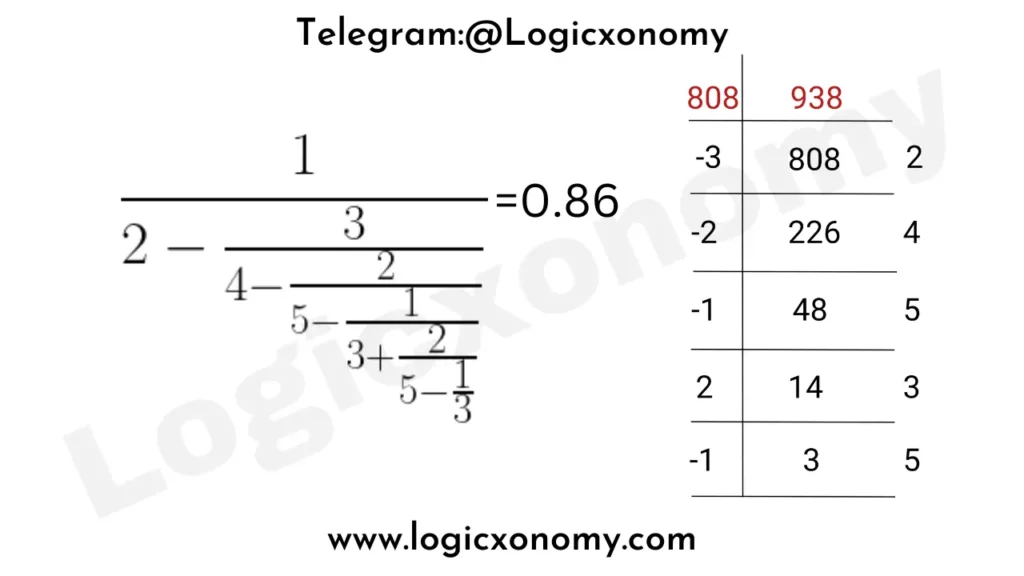
Que 4: Find the value of x+y
\frac{1}{3-\frac{4}{x+\frac{2}{3-\frac{1}{2+\frac{y}{4-\frac{1}{5}}}}}}=\frac{806}{1858}.
Step 1: From top to bottom⇒ 3×806-4k= 1858
k=140
From bottom to top⇒ 4×5-1= 19
19×2+5y= 38+5y

Step 2: (38+5y)×3-19=140
y=3

Step 3: (140x)+53×2=806
x=5
x+y=5+3=8

Mixed Fractions
Que 1: 4\frac{11}{36}+3\frac{5}{19}+8\frac{8}{13}-1\frac{7}{12}+2\frac{21}{41}-6\frac{16}{27}=?
(a) 10\frac{284567}{546858}.
(b) 9\frac{375864}{546858}.
(c) 9\frac{215713}{546858}.
(d) 10\frac{723590}{546858}.
Solution: The sum of all whole numbers= 4+3+8-1+2-6= 10
11/36= 0.3
5/19= 0.2
8/13= 0.6
7/12= 0.6
21/41= 0.5
16/27= 0.6
The sum of fractions= 0.3+0.2+0.6-0.6+0.5-0.6= 0.4 (Approximately)
It means the correct answer= 10.4 (Approximately)
10\frac{284567}{546858}=10+\frac{2.84567}{5.46858}=10+\frac{2}{5}=10.4 (Approx.)
Option (a) is correct
Fraction comparison
Method 1: Find the larger fraction (Simplification and approximation)
A=\frac{19}{25}, B=\frac{11}{14}.
Step 1: Equalize the denominator
A=\frac{19}{25}\times\frac{14}{14}, B=\frac{11}{14}\times\frac{25}{25}.
Numerator of A< Numerator of B
So, fraction B is larger
Method 2: \frac{x+a}{y+a}>\frac{x}{y}, \frac{x-a}{y-a}<\frac{x}{y}.
\frac{2}{3}<\frac{3}{4}<\frac{4}{5}<\frac{11}{12}.
Method 3: Find the decimal values of fractions and then compare them.
A=\frac{5}{8}, B=\frac{11}{15}, C=\frac{24}{35}.
A=0.62, B=0.7, C=0.68
A<C<B
Method 4: If the decimal values of two fractions are very close, we use the percentage method.
A=\frac{153}{263}, B=\frac{165}{282}.
Step 1: Find the percentage change in Numerators (Simplification and approximation)
165-153=12
\frac{12}{153}\times 100=\frac{1200}{153}≈8\%.
Step 2: Find the percentage change in Denominators
282-263=19
\frac{19}{263}\times 100=\frac{1900}{263}≈7\%.
Since the percentage increment in Numerator is more than the denominator
Therefore B>A
Que 1: a=153/263, b=165/282, c=137/236, d=175/301
(I) a<c<d<b
(II) a<d<b<c
(III) c<b<d<a
(IV) c<d<a<b
Solution: Choose any three fractions
a=153/263, b=165/282, c=137/236
Here, b>a (already solved)
Option (iii) is correct
Recurring Decimals
These are decimal numbers with a repeating pattern of digits after the decimal point. The pattern repeats indefinitely and is represented by a horizontal line or bar over the repeating part. They can be classified as pure or mixed recurring decimals and are closely related to rational numbers.
Example: 0.3333.., 0.24565656.., etc.
Let, x= 0.\overline{3} or 0.333..
10x=3.33..
10x=3+x
9x=3
x=3/9
Let, y=0.\overline{34} or 0.343434…
100y=34.3434…
100y=34+y
99y=34
y=34/99
Let, z=0.24\overline{56} or 0.24565656..
z=\frac{2456-24}{9900}.
Let, k=12.345\overline{6723} or 12.3456723672367…
k=12+\frac{3456723-345}{9999000}.
Using Decimals in Complex Calculations
Que 1: 2356437891÷13796321698×111235986543÷67421159832=?
(a) 1.57
(b) 0.28
(c) 0.15
(d) 1.03
Solution: (2.356437891÷13.796321698)×(11.1235986543÷6.7421159832)
Use Approximate Values: (Simplification and approximation)
=(2÷13)×(11÷6)
= 11/39
= 0.28
Option (b) is correct.
The highest value of x^(1/x)
The value of x1/x is highest for x=e i.e. 1.4446….
Here, e is the Euler’s Number. It is approximately equal to 2.71828.
e=\sum_{n=0}^{∞}\limits \frac{1}{n!}=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+…..
Question: Write the given numbers in ascending order: 21/2, 31/3, 41/4, 51/5
Solution: 21/2= 41/4
Here, 3 is closest to e so 31/3 is the largest
Ascending order: 51/5< 41/4=21/2< 31/3
Find the Square and Cube root of any number within 10 sec: Click Here

