SI and CI Problems are essential for competitive exams, used to calculate interest on financial transactions. Questions related to these concepts can be tricky and require a good understanding of formulas and concepts. Practicing a variety of problems is essential to prepare for exams.
Installment Problems
Que 1: The Rs 17500 smartphone is available in 5 equated monthly installments after a down payment of Rs 1100. If the rate of simple interest is 15% per annum, then find the installment amount. (SI and CI Problems)
(a) 3280
(b) 3320
(c) 3400
(d) 3600
Solution: The monthly rate of interest= 15\%\times\frac{1}{12}=\frac{5}{4}\%=\frac{5}{400}=\frac{1}{80}.
Note: 1 rs interest per month on the principal of 80.
Amount Payable= 17500-1100= 16400
Let the Principal of 16400= 80k
Total amount after 5 months= Principal+ Interest
=80k+ 5k
=85k
80k=16400
k=205
So, 85k= 205×85 ……..(i)
Let, the amount of each installment is 80x
The first installment of 80x becomes 84x at the end if not paid
The second installment of 80x becomes 83x at the end if not paid
The third installment of 80x becomes 82x at the end if not paid
The fourth installment of 80x becomes 81x at the end if not paid
The last installment is 80x
Total payable amount at the end= (84+83+82+81+80).x
=410x
410x= 85k= 205×85
x=85/2
So, Amount of each installment= 80x= 3400/-
Option (c) is correct.
Que 2: A sum of Rs 100 is lent to be returned in 10 equal monthly installments of Rs 12 each. Find the annual rate of simple interest. (SI and CI Problems)
(a) 52\frac{4}{23}%
(b) 51\frac{12}{23}%
(c) 49\frac{17}{23}%
(d) 50\frac{1}{23}%
Solution: Let the amount of the monthly installment on the principal of Rs.12 be ‘r’
So, the amount of monthly installment on the principal of rs 100= \frac{r}{12}\times 100=\frac{25\times r}{3}.
Total interest paid on 100 rs in 10 months= \frac{250\times r}{3}.
Total amount after 10 months= 100+\frac{250\times r}{3} ……….(i)
The first installment of rs 12 becomes 12+9r at the end if not paid
The second installment of rs 12 becomes 12+8r at the end if not paid
The third installment of rs 12 becomes 12+7r at the end if not paid
…….
The last installment is rs 12
Total Sum= (12+9r)+(12+8r)+(12+7r)+……+(12+r)+12
=12×10+ (0+1+2+3+4+……+9)×r
=120+45×r ……….(ii)
120+45\times r =100+\frac{250\times r}{3}.
r=\frac{12}{23}.
Monthly rate percentage= \frac{r}{12}\times 100= \frac{100}{23}%
Annual rate percentage= \frac{100}{23}\%\times 12=\frac{1200}{23}\%=52\frac{4}{23}\%.
Option (a) is correct.

Que 3: Rohan borrows Rs 3600 for 6 months at 15% per annum simple interest and pays Rs 100, 200, 400, 800, and 1600 at the end of the first to fifth month respectively. Find the amount of his last installment. (SI and CI Problems)
(a) 712.25 ₹
(b) 698.75 ₹
(c) 674.25 ₹
(d) 756.75 ₹
Solution: 15% Annual= \frac{15}{12}\%= \frac{5}{4}\% monthly
\frac{5}{4}\%= \frac{54}{100}= \frac{1}{80}.
It means 1 rs monthly interest on a principal of 80 rs.
In 6 months, the amount of 3600 rs becomes= 3600+3600\times\frac{1}{80}\times 6=3870 rs
In five months, 100 rs becomes=100+100\times\frac{1}{80}\times 5=(100+6.25) rs
In four months, 200 rs becomes=200+200\times\frac{1}{80}\times 4=(200+10) rs
In three months, 400 rs becomes=400+400\times\frac{1}{80}\times 3=(400+15) rs
In two months, 800 rs becomes=800+800\times\frac{1}{80}\times 2=(800+20) rs
In one month, 1600 rs becomes=1600+1600\times\frac{1}{80}\times 1=(1600+20) rs
Total= (100+200+400+800+1600)+(6.25+10+15+20+20)
=3171.25 rs
The amount of the last installment= 3870-3171.25= 698.75 rs
Option (b) is correct.
Que 4: Ram and Shyam borrowed the same amount of Rs 12820 for 3 years at 10% per annum, to be repaid in annual installments so that the 1st installment is half of the 2nd and the 2nd is two-thirds of the 3rd. If Ram borrows on Compound Interest and Shyam borrows on Simple interest, find the approximate difference between their first installments. (SI and CI Problems)
(a) 63 rs
(b) 58 rs
(c) 81 rs
(d) 43 rs
Solution: The ratio between three installments= 1: 2: 3
Case (I): Ram borrows on Compound Interest (SI and CI Problems)
The principal is divided into three parts in such a way that the amount of installment along with interest becomes equal at the end of the respective years.
10%= 1/10
This means an annual interest of Re 1 on a principal of Rs 10⇒
| Principal | Amount (Instalment) | |
| 1st | 10 | 11 |
| 2nd | 102 | 112 |
| 3rd | 103 | 113 |
But the Installments are in the ratio of 1:2:3 (SI and CI Problems)
So first, equalize them and then multiply by 1, 2, and 3 respectively.
Step 1:
(10: 11)× 112 = 1210: 1331
(102: 112)× 11 =1100: 1331
(103: 113) =1000: 1331
Step 2:
(1210: 1331)×1 =1210: 1331
(1100: 1331)×2 =2200: 1331×2
(1000: 1331)×3 =3000: 1331×3
The total amount of Principal= (1210+2200+3000)×k =6410×k
Here k is a constant
6410×k= 12820
k=2 (SI and CI Problems)
So, the first installment= 1331×k =1331×2= 2662 rs
Case (II): Shyam borrows on Simple Interest
Let, the amount of installments be 100x, 200x and 300x
The first installment of 100x becomes 120x at the end (In 2 years), if not paid
The second installment of 200x becomes 220x at the end (In 1 year) if not paid
The last installment= 300x
Sum total= 120x +220x +300x= 640x
In three years 12820 beocmes= 12820+ 30% of 12820
640x= 12820×130%
640x= 1282×13
x=\frac{1282\times 13}{640}.
The amount of 1st installment= 100x =2604.0625
The difference between instalments= 2662- 2604.0625 =57.9375
The required answer= 58 (approximately)
Option (b) is correct.
Que 5: A smartphone for Rs 20000 is available in 6 monthly installments of Rs 3500. Find the annual rate of simple interest. (SI and CI Problems)
(a) 14.28%
(b) 16.71%
(c) 17.78%
(d) 19.36%
Solution: Let the amount of monthly interest on 3500 rs is ‘r’
The 1st installment of 3500 becomes 3500+5r at the end (In 5 years) if not paid
The 2nd installment of 3500 becomes 3500+4r at the end (In 4 years) if not paid
The 3rd installment of 3500 becomes 3500+3r at the end (In 3 years) if not paid
The 4th installment of 3500 becomes 3500+2r at the end (In 2 years) if not paid
The 5th installment of 3500 becomes 3500+r at the end (In 1 year) if not paid
The last installment is 3500 rs (SI and CI Problems)
Total sum= 3500×6 +15r= 21000+15r
3500⇒ r
1⇒ \frac{r}{3500}.
20000⇒ \frac{r}{3500}\times 20000=\frac{40\times r}{7}.
6-month interest on 20000⇒\frac{40r}{7}\times 6=\frac{240r}{7}.
Total sum= 20000+\frac{240r}{7}.
21000+15r= 20000+\frac{240r}{7}.
r= \frac{7000}{135}.
The monthly rate of interest= \frac{r}{3500}\times 100=\frac{40}{27}.
The Annual rate of interest= \frac{40}{27}\times 12=17.78%
Option (c) is correct.
Que 6: If Anil has to pay Rs. 9,048 to Ramesh in 5 annual installments at the rate of 8% per annum simple interest, what will be the amount of each annual installment paid by Anil to Ramesh?
(a) 1560 rs
(b) 1300 rs
(c) 1415 rs
(d) 2184 rs
Solution: Let each installment= 100x
132x + 124x + 116x + 108x + 100x = 9048
580x = 9048
x=15.6
Installment amount= 100x=1560 rs
Option (a) is correct.
Que 7: If X pays Rs. 4600 to Y in two equal annual installments at a rate of 30% compound interest, what will be the difference between the amounts paid by X if the same amount has to be paid to Y at the same rate of simple interest?
(a) 240
(b) 270
(c) 300
(d) 360
Solution: 30%=3/10
Case1: Compound interest
First installment⇒(10:13)×13=130:132
Second installment⇒102:132
Principal= 130+100=230 unit=4600
1 unit=20
Total installment= 2×132 unit=2×169×20=6760
Case2: Simple interest
10x⇒13x
10x⇒10x
23x=160% of 4600
x=320
Each installment=10x=3200
Total Interest= 6400
Difference= 6760-6400=360 rs
Option (d) is correct.
Que 8: If Surekha borrowed a sum of money and returned it in two equal annual installments of Rs. 5,547 each, at a rate of 7.5% per annum compounded yearly, what was the total amount of interest paid by her?
(a) 1134 rs
(b) 1144 rs
(c) 1126 rs
(d) 1096 rs
Solution: 7.5%=3/40
First installment⇒(40:43)×43
Second installment⇒402:432
Given, 432 unit=5547
1 unit= 3
Prinicipal= 40×(43+40) unit=40×83×3=9960
Total Installments= 5547×2=11094
Interest= 11094-9960=1134 rs
Option (a) is correct.
Que 9: Mr. Dutta wants to deposit his retirement benefit of Rs. 3 lakhs partly in a post office and partly in a bank at 10% and 6% per annum interest rates, respectively. If his monthly interest income is Rs. 2000, what is the difference between the amounts deposited by him in the post office and the bank?
(a) 100000 rs
(b) 50000 rs
(c) 40000 rs
(d) Nil
Solution: 2000 is 2/3% of 3 lakh
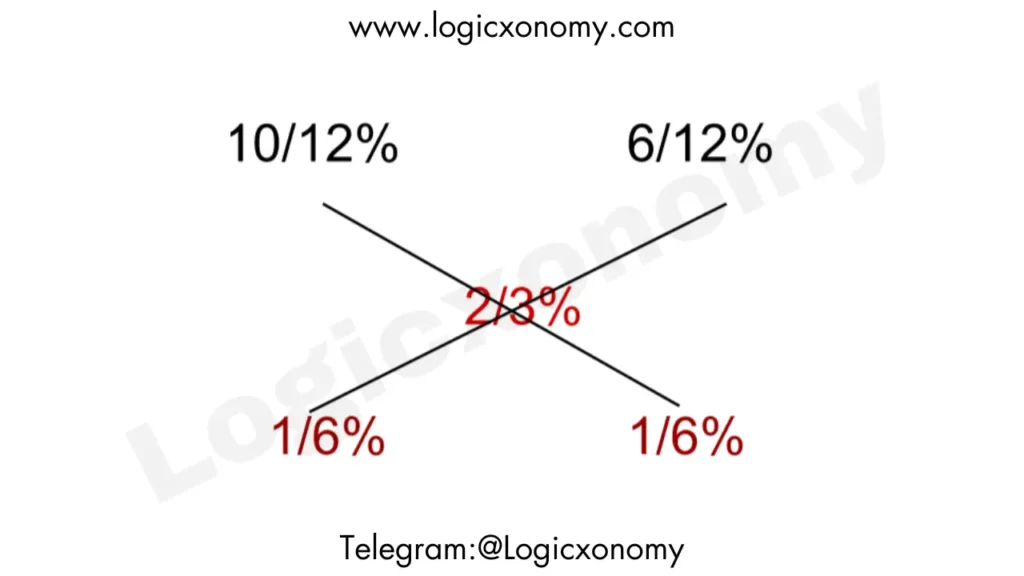
So, both amounts are equal.
Option (d) is correct.
Que 10: A man purchases a scooter by making a cash down payment of Rs. 16224 and agreeing to pay two more annual installments of equal amounts in the next two years. If the rate of interest is 4% per annum, compounded yearly, what is the cash value of the scooter?
(a) 42218
(b) 46824
(c) 52280
(d) 60400
Solution: 4%=1/25
First installment⇒(25:26)×26
Second installment⇒252:262
Given 262 unit=16224
1 unit= 24 rs
Prinicipal= 25×(25+26) unit=25×51×24=30600
The value of scooter= 30600+16224=46824 rs
Option (b) is correct.
Assignment:1
Que 1: What is the annual interest rate at which an investment of 3000 rs will grow to 3993 rs after 3 years, assuming the interest is compounded annually?
(a) 9%
(b) 10%
(c) 11%
(d) 13%
Solution: 3000: 3993
1000: 1331
Cube root both sides⇒ ∛1000: ∛1331= 10:11
Annual interest rate= 10%
Option (b) is correct.
Que 2: What will be the compound interest earned on an investment of 10,000 rs at a rate of 4% per annum, compounded half-yearly, over a period of 2 years?
(a) 636.80 rs
(b) 824.32 rs
(c) 912.86 rs
(d) 828.82 rs
Solution: 4% per annum= 2% half yearly
10000⇒ 10000+200=10200
10200⇒ 10200+204=10404
10404⇒ 10404+208.**=10612.**
10612⇒ 10612+212.**= 10824.**
Option (b) is correct.
Que 3: If a certain amount of money grows to 10648 rs in 3 years and 9680 rs in 2 years with compound interest, what is the annual interest rate?
(a) 5%
(b) 10%
(c) 15%
(d) 20%
Solution: 9680: 10648
1210: 1331⇒ Difference or CI= 121
Option (b) is correct.
Que 4: What is the annual interest rate at which an investment of 2304 rs will grow to 2500 rs in 2 years with compound interest?
(a) 4(1/2)%
(b) 4(1/3)%
(c) 4(1/5)%
(d) 4(1/6)%
Solution: 2304:2500
Square root both sides⇒ √2304: √2500= 48: 50
Interest rate= 200/48= 25/6= 4(1/6)%
Option (d) is correct.
Que 5: Assuming a compound interest rate of 4% per annum for the first year, 5% per annum for the second year, and 6% per annum for the third year, what will be the total compound interest earned on an investment of 10,000 rs for 3 years?
(a) 1600
(b) 1625.80
(c) 1575.20
(d) 2000
Solution: 10000⇒ 10000+400=10400
10400⇒ 10400+520= 10920
10920⇒ 10920+ 654.**=11574.**
CI= 1574.**
Option (c) is correct.
Que 6: What is the total compound interest earned on an investment of 8,000 rs at a rate of 15% per annum for a period of 2 years and 4 months, assuming the interest is compounded annually?
(a) 2980 rs
(b) 3091 rs
(c) 3109 rs
(d) 3100 rs
Solution: 8000⇒ 8000+1200=9200
9200⇒ 9200+1380=10580
10580⇒ 10580+ 529=11109 (5% rate)
CI= 11109-8000= 3109 rs
Option (c) is correct.
Que 7: Given a rate of 5% per annum, if the difference between the compound interest and simple interest earned on a sum of money over a period of 3 years is 36.60 rs, what is the value of the sum of money?
(a) 8000 rs
(b) 8400 rs
(c) 4400 rs
(d) 4800 rs
Solution: 5%=1/20
Compound interest
203: 213= 8000: 9261
CI= 1261 unit
Simple interest
8000⇒8000+400×3
SI=1200
61 unit= 36.60 rs
1 unit= 0.6
Principal= 8000 unit= 8000×0.6= 4800 rs
Option (d) is correct.
Que 8: What is the annual interest rate if the compound interest earned on a specific amount of money over a period of 2 years is 282.15 and the corresponding simple interest earned over the same period is 270?
(a) 6.66%
(b) 10%
(c) 9%
(d) 12.5%
| Principal | 1st Year | 2nd Year |
| 135 | 135 | |
| 12.15 |
Rate %= 12.15×100/135= 9%
Option (c) is correct.
Que 9: If an amount increases by 100% over a period of 8 years at a certain simple interest rate, what will be the compound interest earned on a principal of 8000 after 2 years at the same rate of interest?
(a) 2500 rs
(b) 2000 rs
(c) 2250 rs
(d) 2125 rs
Solution: Annual interest rate= 100/8= 12.5%
12.5%=1/8
For 2 years at CI⇒ 82: 92=64: 81
Principal= 64 unit= 8000
1 unit= 1000/8
CI= 81-64= 17 unit= 17000/8= 2125 rs
Option (d) is correct.
Que 10: A person borrowed a certain amount of money from a private organization at a simple interest rate of 5% per annum. He lent out 50% of this amount to another individual at a compound interest rate of 10% per annum. As a result, he earned a profit of Rs. 3,205 in 4 years. What was the initial amount borrowed by the person?
(a) 80,000
(b) 1,00,000
(c) 1,20,000
(d) 1,50,000
Solution: 10%=1/10
For the amount lent on CI⇒104: 114= 10000: 14641
Total Prinicipal= 20000
Payable SI= 4×5% of 20,000= 4000
Profit= 4641-4000=641 unit
641 unit= 3205
1 unit= 5 rs
Initial amount= 20,000 unit= 1 lack
Option (b) is correct.
Assignment:2
Que 1: What is the ratio of compound interest in the 2nd and 3rd years if the compound interest in the first and second years are in the ratio of 8:27, and the interest rates in the three years are in the ratio of 1:3:6?
(a) 1:2
(b) 4:11
(c) 3:10
(d) Data insufficient
Solution: According to the question the interest in the 1st year= 8 (SI and CI Problems)
The interest in the second year= 27
Since, r% of P=8
3r% of P=24
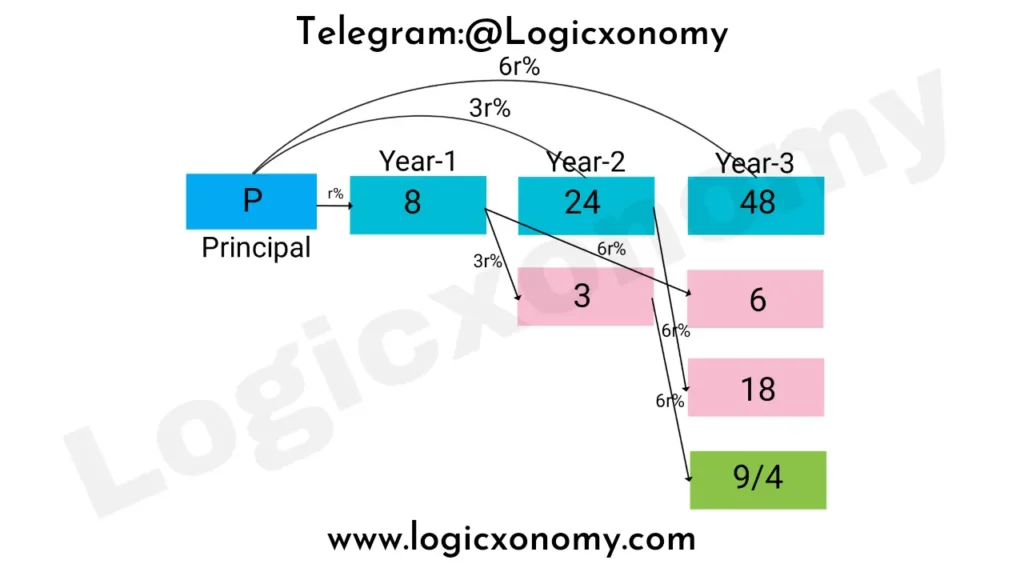
Now, 3r% of 8= 27-24=3
The interest in 3rd year= 6r% of P+ 6r% of 8+ 6r% of 24+ 6r% of 3
= 48+6+18+9/4
=297/4
Ratio between 2nd and 3rd year CI= 27: 297/4
=1: 11/4
=4: 11 (SI and CI Problems)
Option (b) is correct.
Que 2: A and B borrowed money in the ratio 2: 1 respectively for 3 years. A borrowed at 14.28% per annum compound interest and B at 16.67% simple interest. If the interest paid by A is Rs 4056, then find the principal amount with B.
(a) 4116 ₹
(b) 5411 ₹
(c) 3857 ₹
(d) 4564 ₹
Solution: A and B borrowed money in the ratio 2: 1 respectively for 3 years.
14.28%=1/7
16.67%=1/6
Three years CI⇒ 73:83= 343:512
Three years SI⇒ 6:6+3=6:9
Step 1: Equalize the principal amount (SI and CI Problems)
(343:512)×6= 2058:3072
(6:9)×73=2058:3087
Step 2: The ratio of the Principal amounts is 1:2
(2058:3072)×2=4116:6144 ⇒Interest=2028
(2058:3087)×1=2058:3087 ⇒Interest=1029
Give, 2028k= 4056
k=2
So, The Principal amount with B= 2058k= 4116 rs
Option (a) is correct.
Que 3: What would be the difference in the total amount earned as compound interest on a principal of 5,000 for 1.5 years at an annual rate of 4%, if the interest is compounded yearly or half-yearly?
(a) 2.04 rs
(b) 3.06 rs
(c) 8.30 rs
(d) 4.80 rs
Solution: Interest compounded yearly
5000⇒5000+4%= 5200
5200⇒5200+2%= 5304
Interest compounded half yearly
5000⇒5000+2%=5100
5100⇒5100+2%=5202
5202⇒5202+2%=5306.04
Difference= 2.04 rs
Option (a) is correct.
Que 4: If a sum of money doubles itself in 4 years at compound interest, at the same rate of interest, how many years will it take to grow to 8 times its original value?
(a) 18 years
(b) 12 years
(c) 16 years
(d) 24 years
Solution: ×2⇒ 4 years
×23⇒ 4×3=12 years
Option (b) is correct.
Que 5: If a sum of money becomes eight times itself in 3 years at compound interest, what is the rate of interest per annum?
(a) 100%
(b) 80%
(c) 50%
(d) 20%
Solution: ∛1: ∛8= 1:2 (100% increment in one year)
Option (a) is correct.
Que 6: If the amount after 3 years at compound interest compounded annually is 3.375 times the initial sum, what is the rate of interest per annum?
(a) 25%
(b) 50%
(c) 16.67%
(d) 33.33%
Solution: 0.375=3/8
In three years⇒ 1: 3+⅜= 1:27/8= 8:27
In one year⇒ ∛8: ∛27= 2:3
Rate of interest= 50%
Option (b) is correct.
Que 7: If an amount of money appreciates to 7,000 after 4 years and to 10,000 after 8 years at a certain compound interest compounded annually, what was the initial amount of money?
(a) 4700 rs
(b) 4900 rs
(c) 4100 rs
(d) 4300 rs
Solution: 1st: 4th= 4th: 8th
1st: 7000= 7: 10
1st×10=49000
1st=4900
Option (b) is correct.
Que 8: At an annual interest rate of 12% compounded monthly, which of the following equations can be solved to find the number of years, y, that it would take for a certain investment to increase by a factor of 64?
(a) 64= (1.01)12y
(b) 1/64= (1.04)×12y
(c) 64= (1.04)×12y
(d) 8= (1.01)×6y
Solution: A=P(1+r/100)n formula
P=1
A=64
r=1% monthly
n=12y months
Option (a) is correct.
Que 9: If a sum of money is invested at 20% compound interest (compounded annually) and it would fetch Rs. 723 more in 2 years if the interest is compounded half-yearly, what is the initial sum invested?
(a) 15000 rs
(b) 30000 rs
(c) 20000 rs
(d) 7500 rs
Solution: 10% half yearly for 4 years
104: 114= 10000: 14641
20% yearly for 2 years
10000⇒ 10000+44%= 14400
Difference= 14641-14400= 241
241 unit= 723
1 unit= 3
10000 unit= 30000 rs
Option (b) is correct.
Que 10: If the compound interest on a certain sum for 2 years at 10% per annum is Rs. 525, what is the simple interest on the same sum for double the time at half the rate percent per annum?
(a) 520 rs
(b) 550 rs
(c) 500 rs
(d) 515 rs
Solution: 21% of P=525
100% of P=P= 2500
Simple interest for 4 years at 5% annual= 20% of P= 500
Option (c) is correct.

