Right Angle triangle Theorems (50 Powerful exam hack)

In this chapter, we are going to discuss important right angle triangle theorems and properties along with their proofs.

Basic Formulas

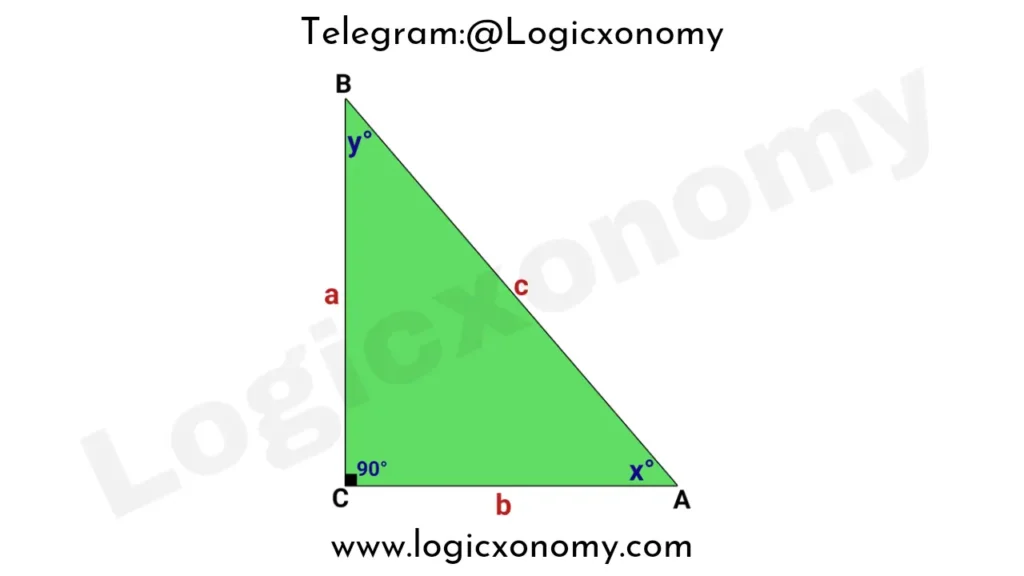
△ABC is a right triangle where ∠C=90°, and lengths of the sides BC, CA, and AB are a,b, and c respectively. 

∠A=x° and ∠B=y°

So, x+y=90 ………(i)

Draw CH⟂AB where the height CH=h

In the right △AHC,

∠ACH=90°-∠HAC=y°    …..From equation (i)

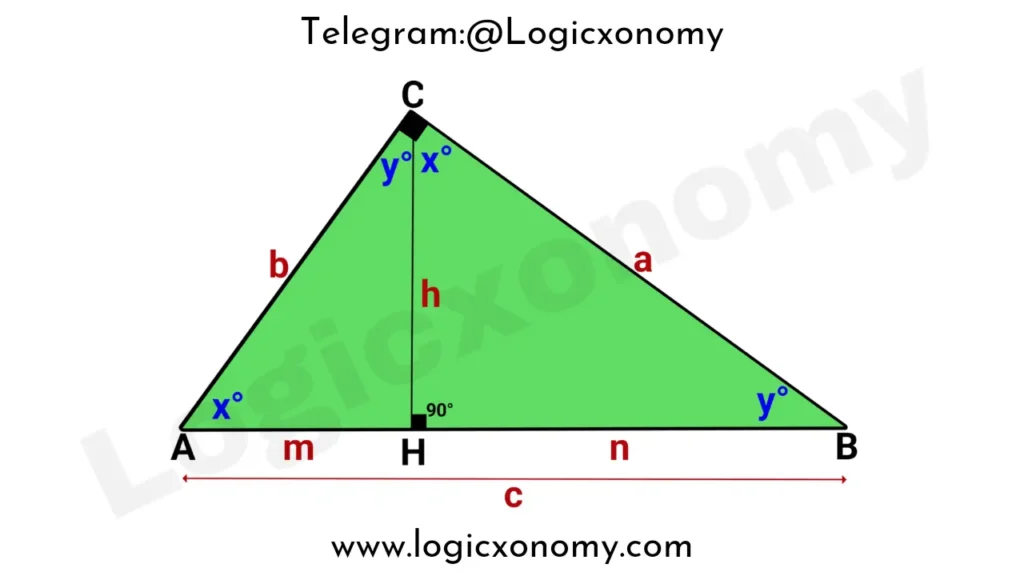
Similarly, In the right △BHC,

∠BCH=90°-∠HBC=x°    …..From equation (i)

Let, AH=m and BH=n

Now, △AHC~△CHB (Similar Triangles)

\frac{CH}{AH}=\frac{BH}{CH}.

\frac{h}{m}=\frac{n}{h}.

h^2=m\times n …….(iii)

△CHB~△ACB (Similar Triangles)

\frac{AH}{AC}=\frac{AC}{AB}.

\frac{m}{b}=\frac{b}{c}.

b^2=m\times c …….(iv)

△AHC~△ACB (Similar Triangles)

\frac{BH}{BC}=\frac{BC}{AB}.

\frac{n}{a}=\frac{a}{c}.

a^2=n\times c …….(v)

Add equations (iv) and (v):

a^2+b^2=c\times (m+n).

a^2+b^2=c^2 ………(vi)

In the right △AHC, 

Sin(A)=\frac{CH}{AC}.

Sin(x)=\frac{h}{b} ………(vii)

In the right △BHC, 

Sin(B)=\frac{CH}{BC}.

Sin(y)=\frac{h}{a}. 

Sin(90°-x)=\frac{h}{a}.

Cos(x)=\frac{h}{a} ………(viii)

From equations (vii) and (viii):

Sin^{2}x+Cos^{2}x=1   (Trigonometric identity)

\frac{h^2}{b^2}+\frac{h^2}{a^2}=1.

\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{h^2} ………(ix)

The Area of the right angle triangle= \frac{1}{2}\times Base\times Height.

\frac{1}{2}\times b\times a=\frac{1}{2}\times c\times h.

 a\times b=c\times h ………..(x)

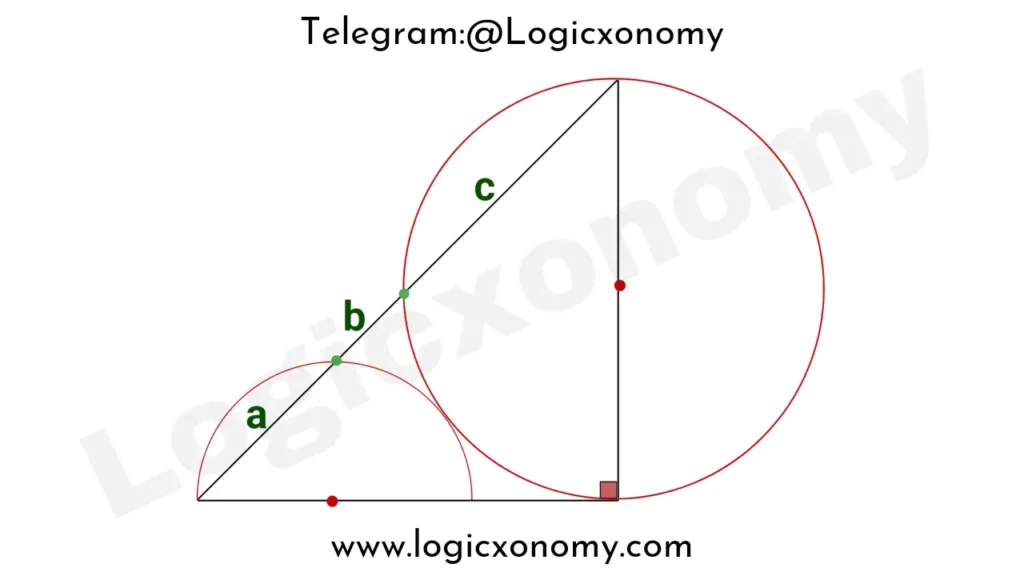
Trisection of hypotenuse

In the given figure, the hypotenuse of a right-angled triangle is trisected by two circles. If the lengths of these segments are a, b, and c respectively. Then prove:

\frac{a}{b}\times\sqrt{\frac{c}{a+b}}=2

Let the lengths of the sides PQ, QR, and PR of △PQR be y, x, and z respectively. The length of the radius of the smaller semicircle is r.

Let ∠QPR=θ

Therefore ∠QRP=90°-θ

Draw ST and QU

Then ∠STP and ∠QUR=90°  

Theorem: The angle subtended by a diameter of a circle at any point on its boundary is 90°

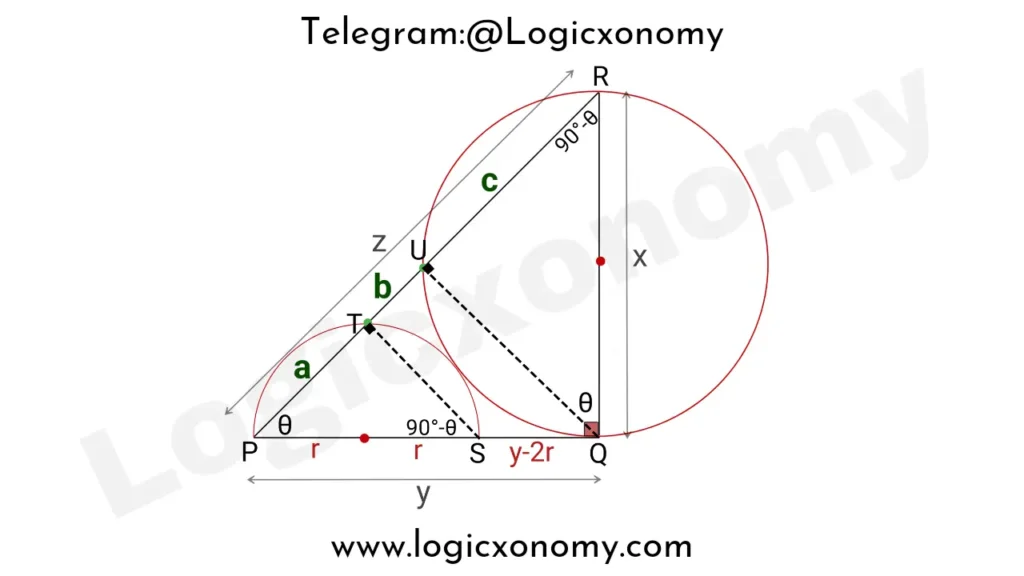
So, ∠PST=90°-θ and ∠UQR=θ

PQ is the tangent and PR is the secant of the larger circle, so by theorem

PQ²=PU×PR

y²=(a+b)×z

(a+b)=\frac{y^2}{z}……..(i)

△QUR~△PQR (Similar Triangles)

\frac{UR}{RQ}=\frac{RQ}{PR}.

\frac{c}{x}=\frac{x}{z}.

c=\frac{x^2}{z} …….(ii)

△PST~△PQU (Similar Triangles)

\frac{PT}{TU}=\frac{PS}{SQ}.

\frac{a}{b}=\frac{2r}{y-2r} …….(iii)

Now draw VW, here V and W are the centers of the respective circles.

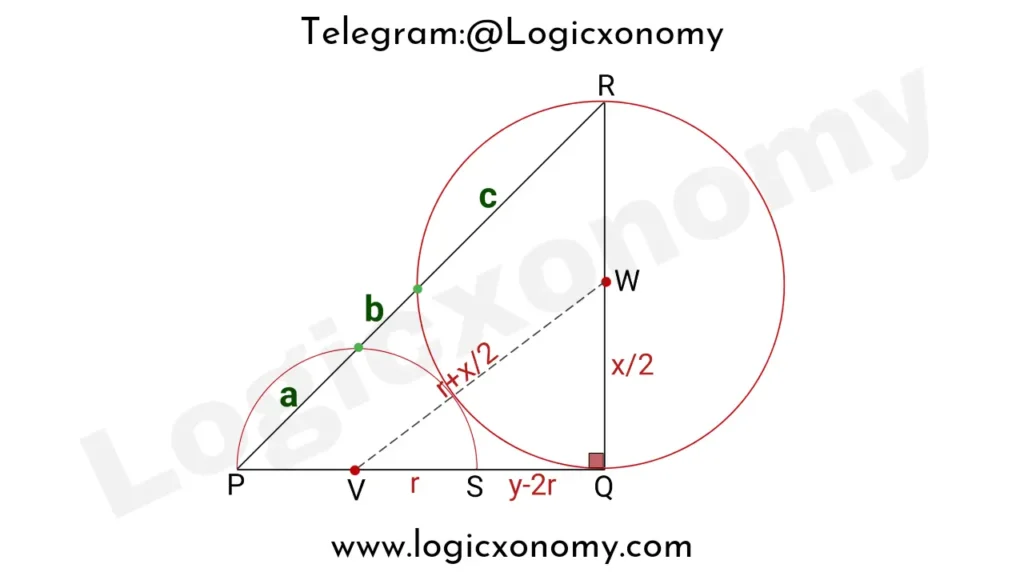
In the right triangle △VQW, apply Pythagoras’ Theorem:

VW²=VQ²+QW²

(r+\frac{x}{2})^2=(y-r)^2+(\frac{x}{2})^2.

r^2+\frac{x^2}{4}+rx=y^2+r^2-2yr+\frac{x^2}{4}.

rx=y^2-2yr.

r=\frac{y^2}{x+2y}.

Put this value of r in equation (iii)

\frac{a}{b}=\frac{2r}{y-2r}.

After solving, \frac{a}{b}=\frac{2y}{x} ……(iv)

Now put all the values in the given expression:

\frac{a}{b}\times\sqrt{\frac{c}{a+b}}=\frac{2y}{x}\times \sqrt{\frac{\frac{x^2}{z}}{\frac{y^2}{z}}}.

=\frac{2y}{x}\times \frac{x}{y}=2

Hence Proved…

A square inscribed in a Right Triangle

Case I: If One side of the square lies on the hypotenuse of the right triangle.

In the given right triangle △ABC, the lengths of the sides of the triangle are p, q, and r. A square is inscribed in this triangle such that one of its sides is on the hypotenuse then find the area of the Square.

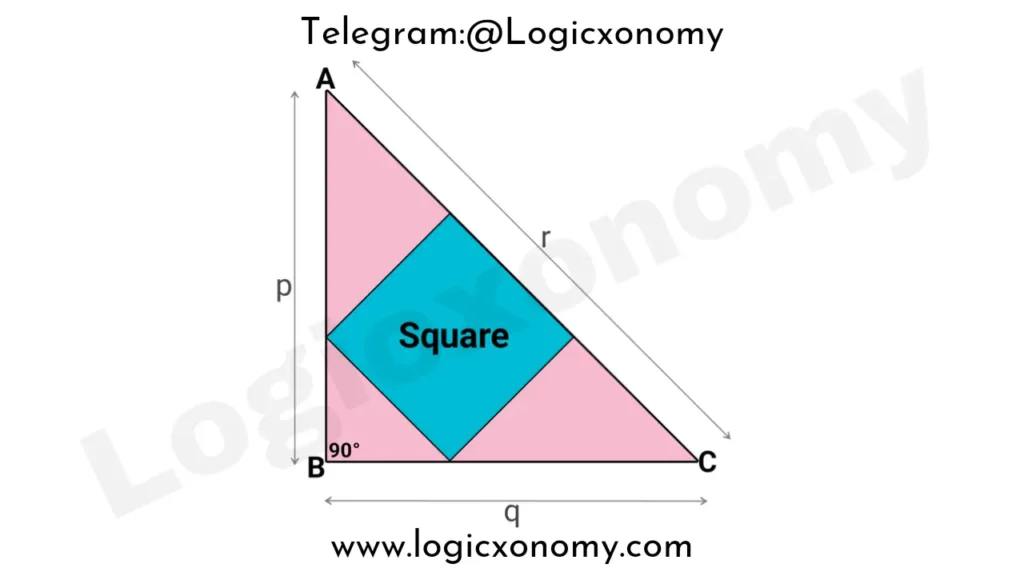
Let, the length of the side of Square is ‘x’ and ∠BCA=θ

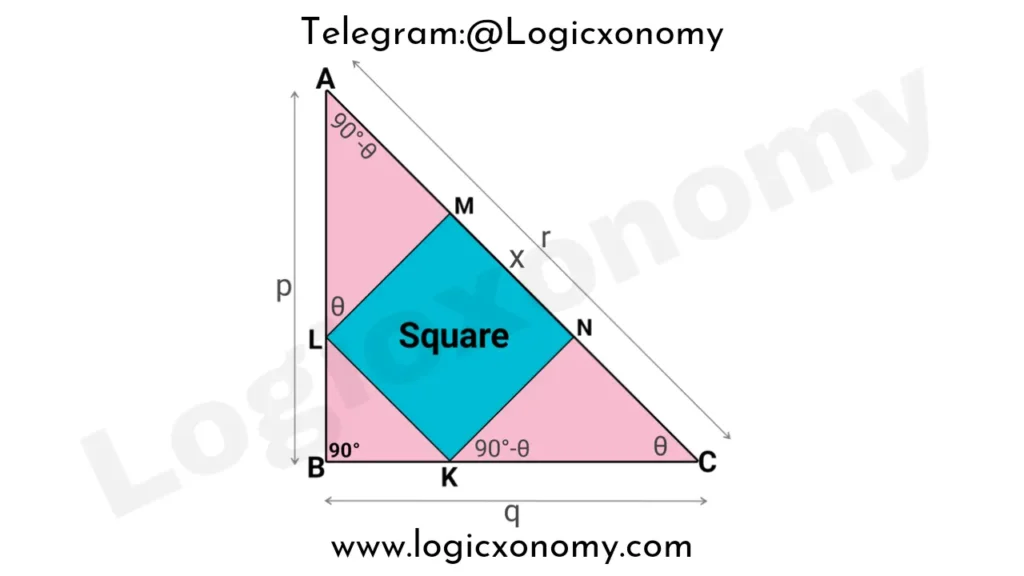
△CNK~△CBA (Similar Triangles)

\frac{NK}{AB}=\frac{NC}{BC}.

\frac{x}{p}=\frac{NC}{q}.

NC=\frac{q}{p}.x …….(i)

△AML~△ABC (Similar Triangles)

\frac{LM}{BC}=\frac{AM}{AB}.

\frac{x}{q}=\frac{AM}{p}.

AM=\frac{p}{q}.x …….(ii)

Now, AM:NC=\frac{px}{q} :\frac{qx}{p}=(\frac{p}{q} :\frac{q}{p})\times pq.

AM:NC=p^2:q^2 …….(iii)

The length of the hypotenuse= r

AM+MN+NC=r

\frac{p}{q}.x+x+\frac{q}{p}.x=r.

x.(\frac{p}{q}+1+\frac{q}{p})=r.

x.(\frac{p^2+pq+q^2}{pq})=r.

x=\frac{pqr}{p^2+pq+q^2}.

Now, the area of the square= x²

Case II: If the sides of the square lie on the base and perpendicular of the right triangle

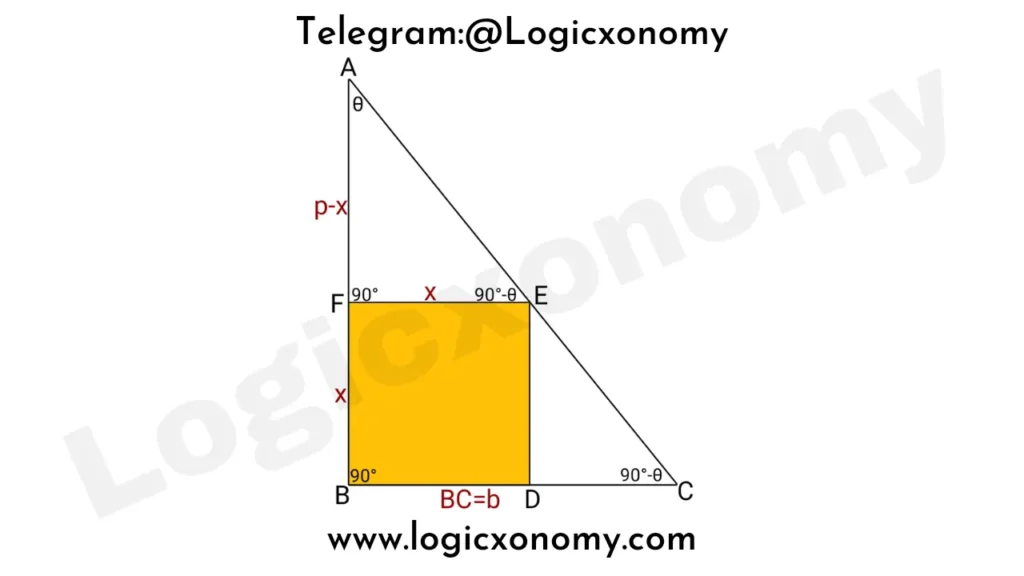
The length of AB=p, BC =q, and the length of the sides of Square is ‘x’.

△AFE~△ABC (Similar Triangles)

\frac{AF}{AB}=\frac{FE}{BC}.

\frac{p-x}{p}=\frac{x}{b}.

pb-bx=px.

x=\frac{pb}{p+b}.

Now, the area of the square= x²

Relation between the heights of the triangles

In the given right angle triangle △ABC in which ∠A=90°, the line segments AD, DP, DR, PQ, and RS are perpendicular to the corresponding sides. Then find the relationship between AD, PQ, and RS.

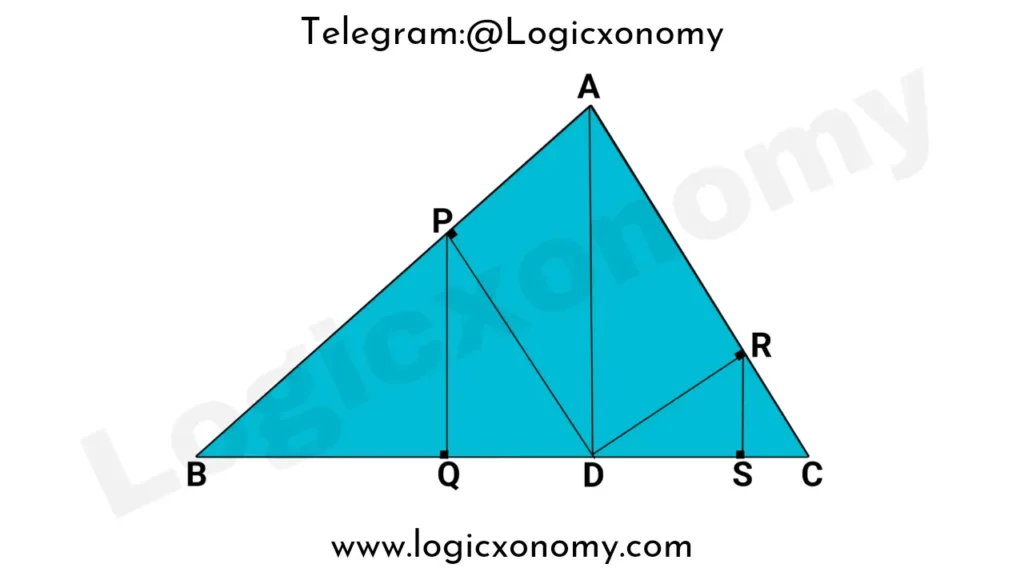
Let, ∠B=θ

APDR is a Rectangle because its all interior angle is 90°

△PQD~△DPA (Similar Triangles)

\frac{QD}{AP}=\frac{PD}{AD}.

PD\times AP=QD\times AD. 

Area of the Rectangle APDR= QD×AD ……….(i)

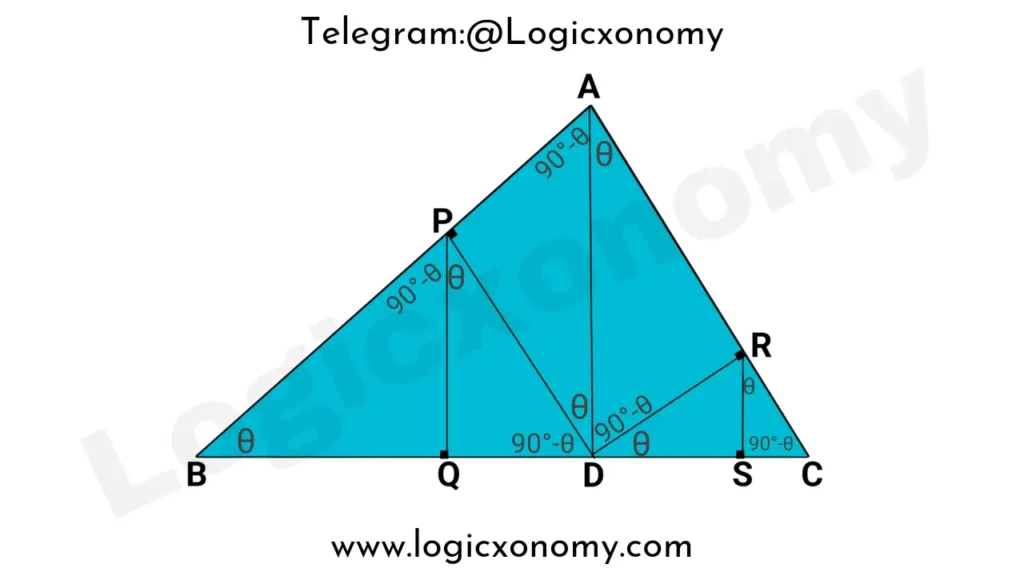
△DSR~△ARD (Similar Triangles)

\frac{DS}{AR}=\frac{DR}{AD}.

AR\times DR=DS\times AD. 

Area of the Rectangle APDR= DS×AD ……….(ii)

Compare equations (i) and (ii)

QD×AD=DS×AD

QD=DS  

Let, QD=DS=x …………(iii)

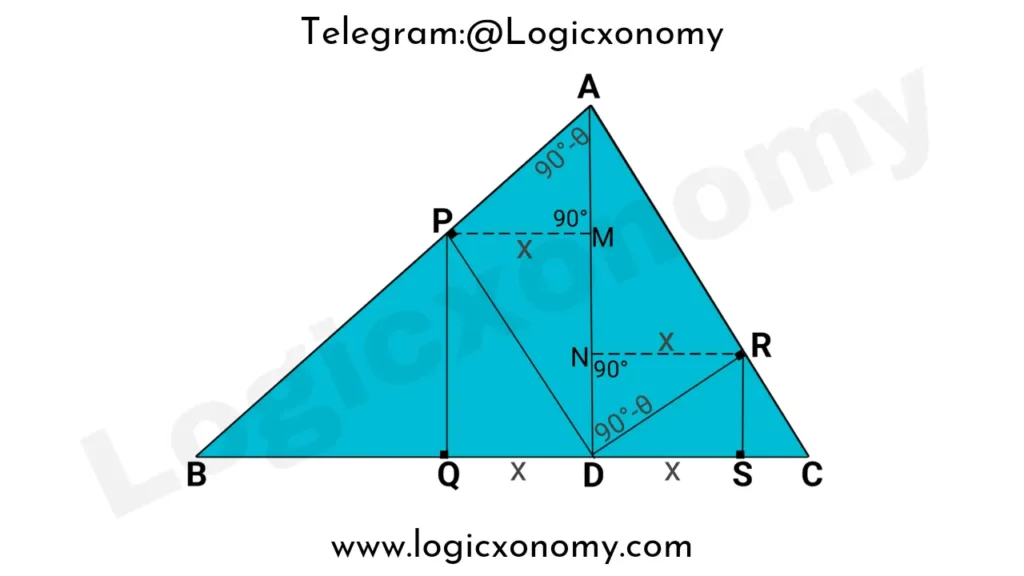
Draw PM and RN, perpendicular to AD.

So, PM=RN=x

△PMA~△RND (Similar Triangles)

\frac{AM}{ND}=\frac{PM}{RN}=\frac{x}{x}.

AM=ND ……..(iv)

AM=ND=RS

MD=PQ

Now, AD=MD+AM

AD=PQ+RS

Que: Find the area of rectangle APDR if AB=4 cm and AC=3 cm.

Solution: Here DP⊥AB and DR⊥AC

As we know in the Right triangle: BC×AD=AB×AC

5×AD=3×4

AD=12/5 cm ……..(i)

In Right Triangle ABC⇒ BD: DC= AB²:AC²=16:9

BD+DC=BC

16k+9k=5

k=1/5

BD=16/5 and DC=9/5

In △BDA⇒ BD×DA=AB×DP

16/5×12/5=4×DP

DP=48/25 cm ………(ii)

Similarly in In △ADC⇒ AD×DC=DR×AC

12/5×9/5=3×DR

DR=36/25 cm …….(iii)

Now, the Area of APDR= DP×DR=2.7648 cm²

Altitude, Angle Bisector, and Median

In the given Right angle △ABC, ∠B=90°. BP is the altitude, BQ is the angle bisector and BR is the median of the triangle then Find PQ: QR

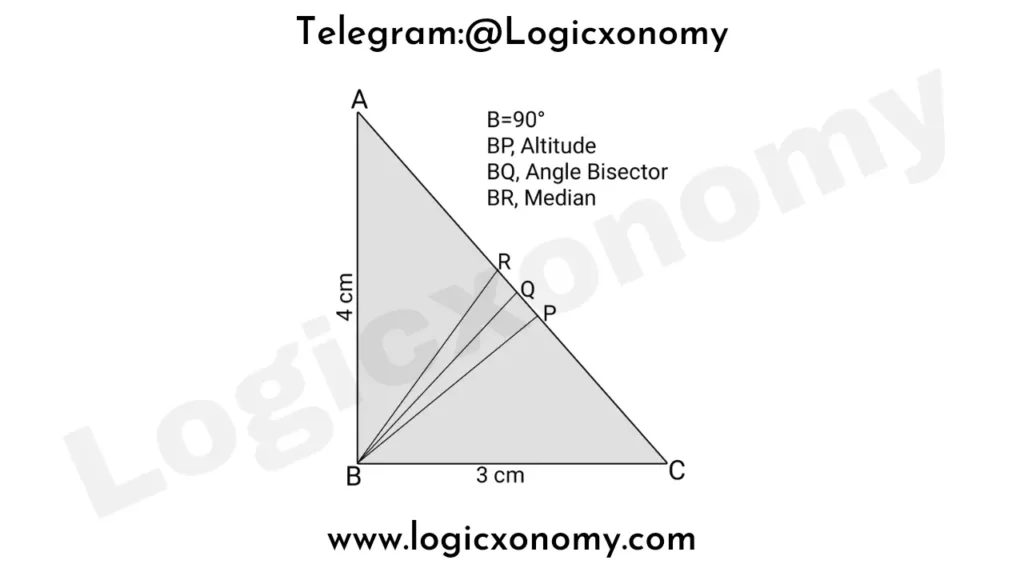
Use Pythagoras’ theorem in this right triangle⇒ AC=5 cm

Property of the Median: AR=RC=BR= 2.5 cm (R is the circumcenter of the triangle)

BR= 2.5 cm ……..(i)

Property of the Altitude: 1/2×BC×AB=1/2×AC×BP

12=5×BP

BP=12/5 ……..(ii)

△ARB is an isosceles triangle (AR=BR)

Let, ∠A=θ

So, ∠ABR=θ

∠ABQ=45° (BQ is the angle bisector)

So, ∠RBQ= ∠ABQ – ∠ABR= 45°-θ …….(iii)

In the right angle △BPC, Since ∠C=90°-θ 

So, ∠CBP=θ

∠QBP= ∠CBQ – ∠CBP= 45°-θ ………(iv)

From equations (iii) and (iv):

BQ is the angle bisector of ∠RBP, so PQ: QR= BP: BR (Angle Bisector Theorem)

PQ: QR= 12/5: 2.5

PQ: QR= (12/5: 2.5)×5= 12: 12.5

PQ: QR=  24:25 

Relation between the radii of circles

In the given right angle △ABC, ∠B=90°. Then the relation between the radii of given circles is: x²=ab

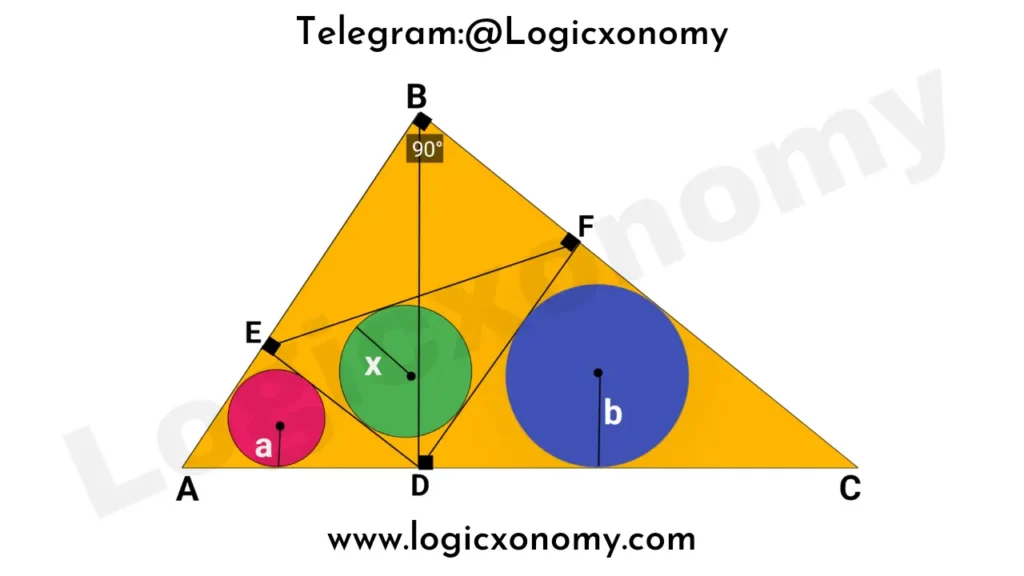
Let, ∠A=θ then ∠ABD=90°-θ

∠EBD=∠EFD=90°-θ (BFDE is a Rectangle)

So, △AED~△EDF~△DFC (Similar Triangles)

\frac{a}{AD}=\frac{x}{EF}=\frac{b}{DC} ………..(i)

Let, AB=p

BC=q

AC=r

Then \frac{1}{2}\times r\times BD=\frac{1}{2}\times p\times q.

BD=EF (Diagonals of the Rectangle)

EF=\frac{pq}{r}.

AD=AB\times Cos(A)=p\times \frac{p}{r}=\frac{p^2}{r}.

DC=BC\times Cos(C)=q\times \frac{q}{r}=\frac{q^2}{r}.

Put these values in equation (I):

\frac{a}{AD}=\frac{x}{EF}=\frac{b}{DC}=k    (k is a constant)

a=AD.k

x=EF.k

b=DC.k

ab=AD.DC.k²=(EF.k)²=x²

The ratio between the sides of a Right Triangle

Que: What is the area of ​the right triangle whose one side is 58 cm and all the sides are integers?

(a) 840 cm²

(b) 24360 cm²

(c) 1160 cm²

(d) None

Solution: The ratio between the sides of a Right Triangle is: 

⇒ (a²-b²): 2ab: (a²+b²)

Here a and b are positive integers

(a²+b²) represents the Hypotenuse of the triangle

If 2ab=58

ab=29

(a,b)=(29,1)

Then the sides⇒ (29²-1²): 2×29×1: (29²+1²)= 840: 58: 842

The area of the triangle= \frac{1}{2}\times 840\times 58=24360 cm²

If (a²+b²)=58

(a,b)=(7,3)

Then the sides⇒ (7²-3²): 2×7×3: (7²+3²)= 40: 42: 58

The area of the triangle= \frac{1}{2}\times 40\times 42=840 cm²

If (a²-b²)=58

(a+b)(a-b)=58

{(a+b), (a-b)}={(58,1), (29,2)}

If a+b=58 and a-b=1

a=29.5 (Not an integer)

If a+b=29 and a-b=2

a=15.5 (Not an integer)

So, only two areas are possible which are 24360 cm² and 840 cm²

Option (d) is correct.

Shaded Area Problems of Geometry: Click Here