Pedal Triangle Properties, theorems and their applications in Geometry. Geometry shortcuts and formulas with proof are given below:
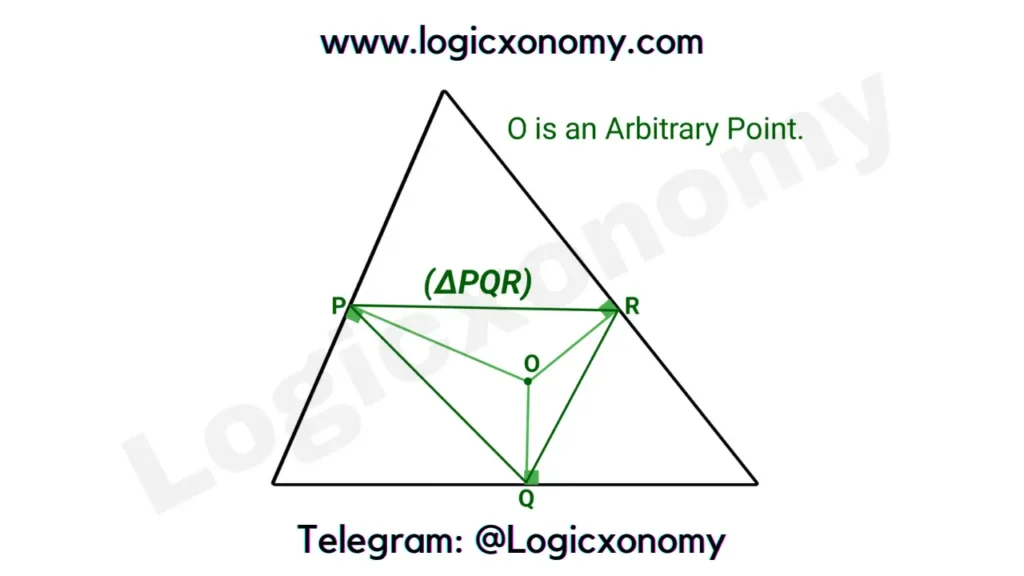
Pedal Triangle: The triangle, whose vertices are the feet of the perpendiculars drawn from an arbitrary point inside the triangle to the sides of the triangle.
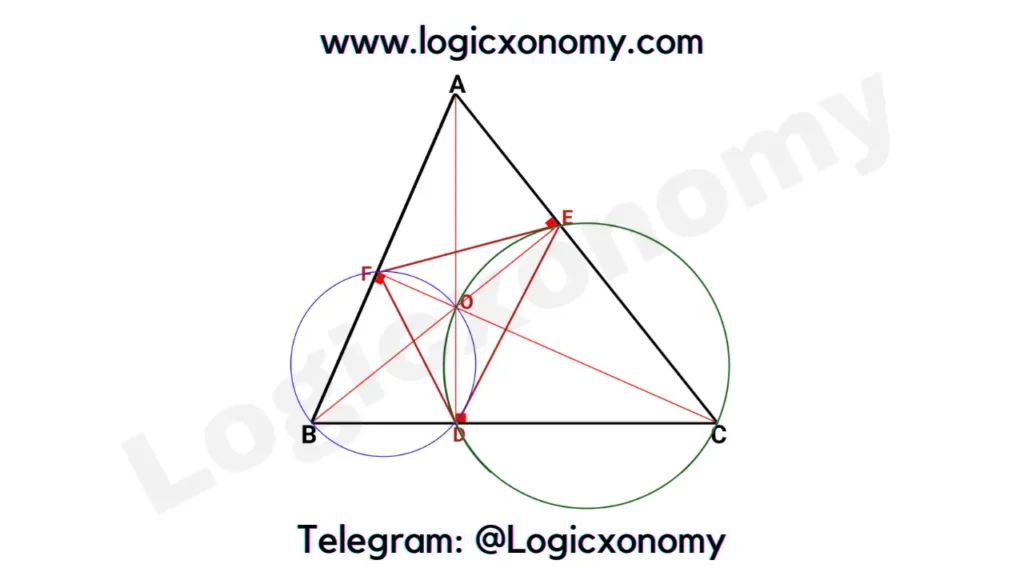
Orthic Triangle: The triangle, formed by joining the feet of the altitudes drawn from the triangle’s vertices to their respective opposite sides.

Pedal triangle Properties
In the given ∆ABC, O is the intersection point of the altitudes of the triangle (Orthocenter of ∆ABC).

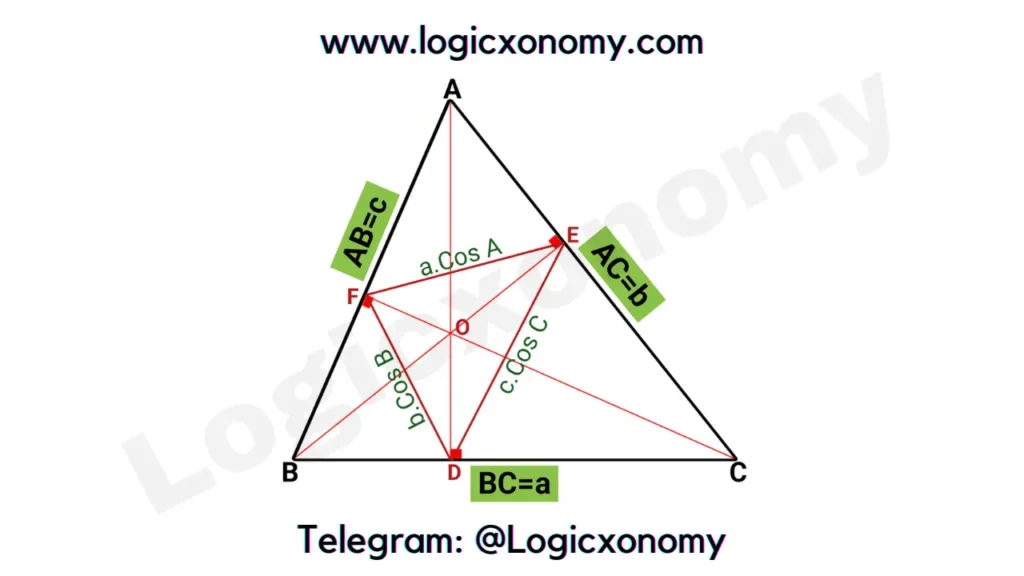
In right angle ∆AEB, ∠AEB=90°
Cos A= AE/AB= AE/c
AE=c.Cos A
Similarly in ∆AFC, AF=b.Cos A
Use the Cosine formula in ∆ABC,
BC²=AB²+AC²-2×AB×AC×Cos A
a²=b²+c²-2bc.Cos A
Similarly in ∆AFE,
FE²=AF²+AE² – 2.AF.AE.Cos A
FE²=b² Cos²A+c² Cos²A – 2bc Cos³A
=Cos²A (b²+c² – 2bc Cos A)
= a² Cos²A
FE=a.Cos A
Similarly, DF=b. Cos B and ED=c.Cos C

Interior Angles of Orthic Triangle
BFOD is a Cyclic Quadrilateral (∠BFO+∠BDO=180°)
In right angle ∆ABE, ∠AEB=90°
So, ∠ABE=90°-A
For chord FO, ∠FBO=∠FDO=90°-A
Similarly, for Cyclic Quadrilateral DOEC, ∠ECO=∠EDO=90°-A
From both equations: ∠FDO=∠EDO=90°-A (OD is the Angle Bisector)
Now we can say that point O is the Incenter of ∆DEF (Intersection point of angle bisectors DO, EO & FO). Whereas O is also the Orthocenter of ∆ABC.
∠FDE=∠FDO+∠EDO=180°-2A=π-2A
∠FDE=π-2A
∠DEF=π-2B
∠DFE=π-2C
Area of Orthic Triangle
Area of ∆DEF=1/2×DF×DE×Sin (∠FDE)
=1/2×b.Cos B× c.Cos C×Sin(180°-2A)
=1/2.bc.Cos B.Cos C. Sin 2A
=1/2.bc.Cos B.Cos C. (2. Sin A.Cos A)
=1/2.bc Sin A (2. Cos A.Cos B.Cos C)
=Area of ∆ABC. (2.Cos A.Cos B.Cos C)
ar(∆DEF)/ar(∆ABC)=2.Cos A.Cos B.Cos C
Circumradius of Orthic Triangle
In the given figure, R is the Circumradius of ∆ABC and X is the Circumradius of ∆DEF.

Apply Sine Rule in ∆ABC
\frac{a}{Sin A}=\frac{b}{Sin B}=\frac{c}{Sin C}=2R.
Similarly for ∆DEF, \frac{FE}{Sin(∠FDE)}=2X.
FE=2X. Sin(180°-2A)
a.Cos A=2X. Sin 2A
a.Cos A=2X. (2. Sin A.Cos A)
a/2.Sin A=2X
R=2X
The perimeter of the Orthic Triangle
The perimeter of ∆DEF=p(∆DEF) and Perimeter of ∆ABC=p(∆ABC)

p(∆DEF)=FE+DF+DE
=a.Cos A+b.Cos B+c.Cos C
=2R.Sin A.Cos A+2R.Sin B.Cos B+2R.Sin C.Cos C
=R (Sin 2A+Sin 2B+Sin 2C)
=R {2.Sin(A+B). Cos(A-B)+Sin 2C}
=R {2.Sin(180°-C). Cos(A-B)+Sin 2C}
=R {2.Sin C. Cos(A-B)+ 2.Sin C.Cos C}
=2R.Sin C {Cos(A-B) +Cos C}
=2R. Sin C [Cos(A-B) +Cos {180°-(A+B)}]
=2R. Sin C {Cos (A-B) – Cos (A+B)}
=2R. Sin C (2.Sin A. Sin B)
=4R. Sin A. Sin B. Sin C
=4R. (a/2R). (b/2R). (c/2R)
=\frac{abc}{2R²}. ……..(R=abc/4∆), Area of the triangle=∆
=\frac{(R.4∆)}{2R²}.
=\frac{2∆}{R}.
=\frac{(2. rs)}{R}. ……..(∆=rs), Inradius of the triangle=r, Semiperimeter=s
=\frac{r.(2s)}{R}. ……..(Perimeter of the triangle=2s)
=\frac{r. p(∆ABC)}{R}.
p(∆DEF) : p(∆ABC)= r : R
Hence Proved…
The Centroid of the Triangle (All Concepts): Click Here

