Incenter of a Triangle: 10 Important Theorems and Formulas with Proofs

The incenter of a triangle is a unique point that holds significant geometric properties. It is the point where the angle bisectors of a triangle intersect, and it is equidistant from the sides of the triangle. This point also lies inside the triangle, unlike the circumcenter, which may lie outside the triangle.

Incenter of the Triangle

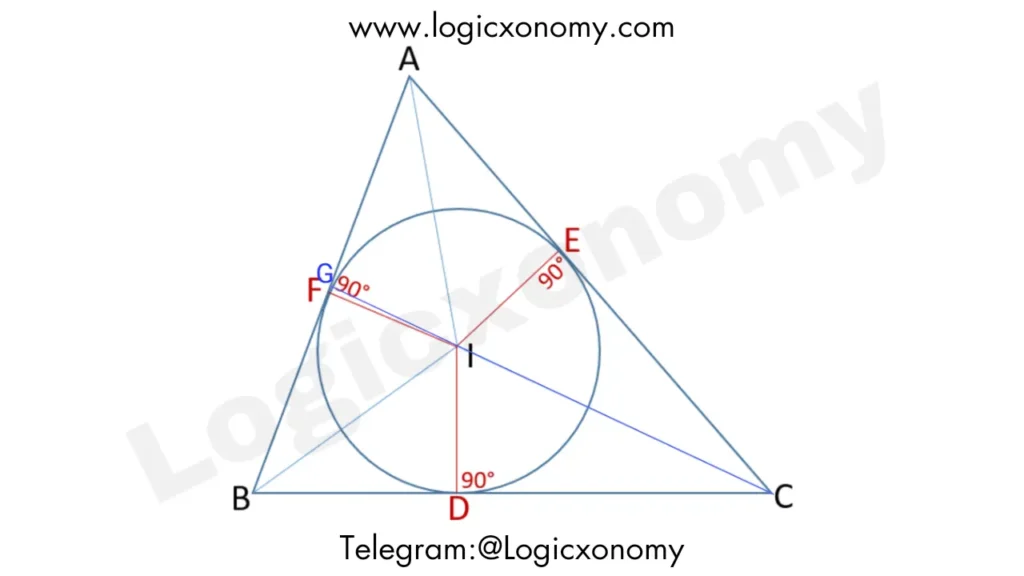
The point of intersection of two or more angle bisectors of a triangle is called the incentre of the triangle. It is denoted by ‘I’, where I is equidistant from all the sides of the triangle. It is the center of the circle that is inscribed inside the triangle and touches all three sides of the triangle. 

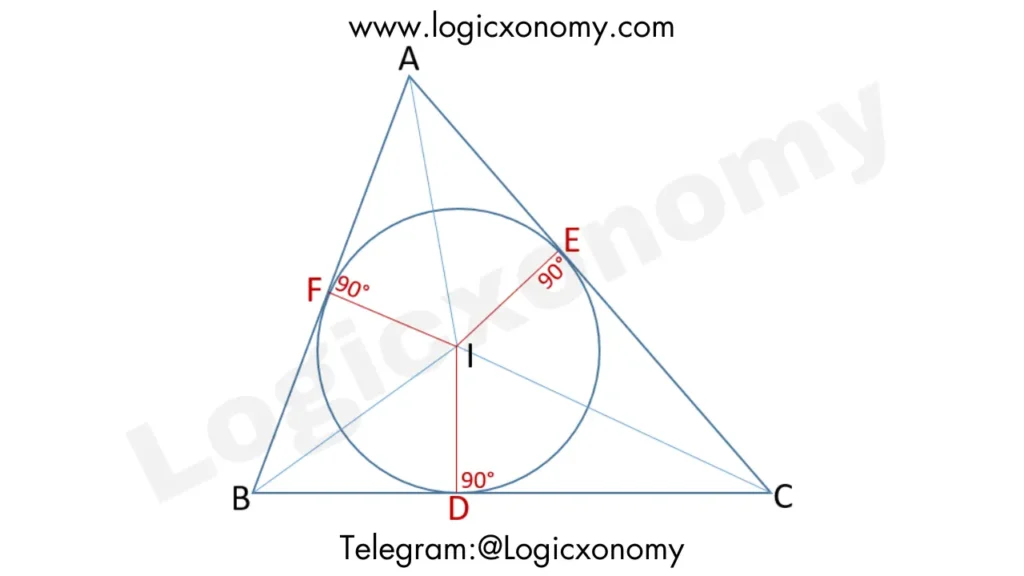
In this given figure: ID=IE=IF=r 

Here ‘r’ is the Inradius of the triangle (Incenter of a triangle) 

△=r×s ………(i)

‘s’ is the Semi-Perimeter of the triangle 

△ is the Area of the Triangle

Inradius of the Triangle Proof

Let BC=a, CA=b, and AB=c

In the given figure: ar(△ABC)= ar(△BIC)+ar(△AIB)+ar(△AIC)

Area of the triangle= ½× Base×Height

△=½×a×r+ ½×b×r+ ½×c×r

△=½×r×(a+b+c)

△=r×s (Incenter of a triangle) 

Here 2s=a+b+c 

Angle Bisector Theorem

The angle bisector drawn from any vertex of a triangle to the opposite side divides that side into segments that are proportional to the adjacent sides of the vertex. (Incenter of a triangle) 

BD: DC=c:b

AE: EC=c:a

BF: FA=a:b

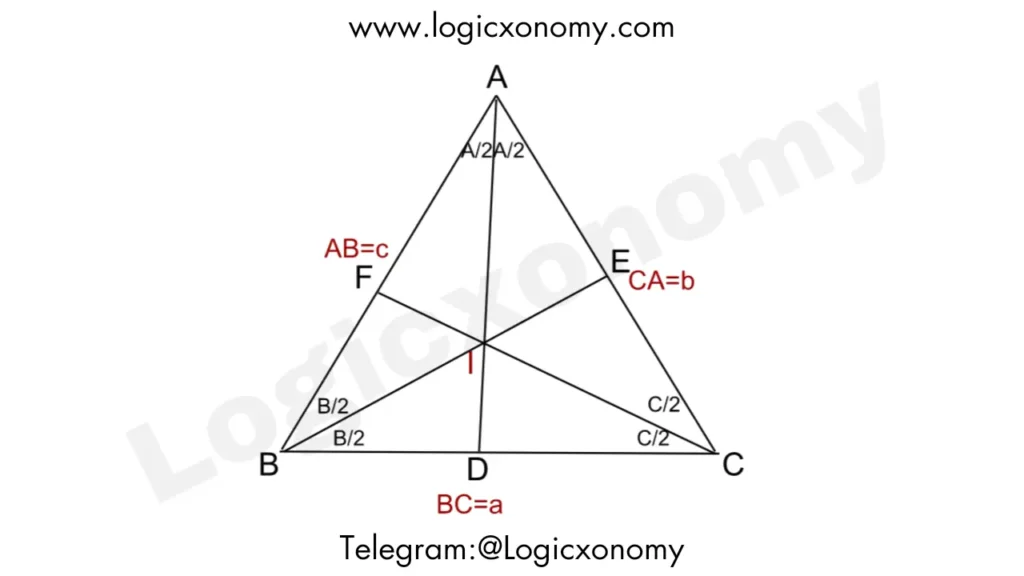
\frac{ar(BAD)}{ar(DAC)}=\frac{\frac{1}{2}\times AB\times AD\times Sin(A/2)}{\frac{1}{2}\times AC\times AD\times Sin(A/2)}.

\frac{BD}{DC}=\frac{AB}{AC}.

BD: DC=c:b …………..(i)

Let BD=ck and DC=bk

BD+DC=(b+c)k= a

k=\frac{a}{b+c}.

BD=\frac{ac}{b+c}.

In △DBA, BI is the angle bisector

So, AI: ID= AB: BD

AI: ID=c:\frac{ac}{b+c}.

AI: ID=b+c: a ………(ii)

Similarly, BI: IE=a+c: b

CI: IF=a+b: c

Angle made at the Incenter

In △BIC, the sum of all interior angles= 180°

B/2+C/2+∠BIC=180°

(180°-A)/2+∠BIC=180°

∠BIC=90°+A/2

Similarly, ∠CIA=90°+B/2

∠AIB=90°+C/2

It means angles made at the incenter are Obtuse Angles. (Incenter of a triangle) 

Inradius of the Right Angle Triangle

In △ABC, B=90° and O is the incenter. So altitudes OD=OE=OF=r

Let BC=b, AB=p, and Hypotenuse AC=h

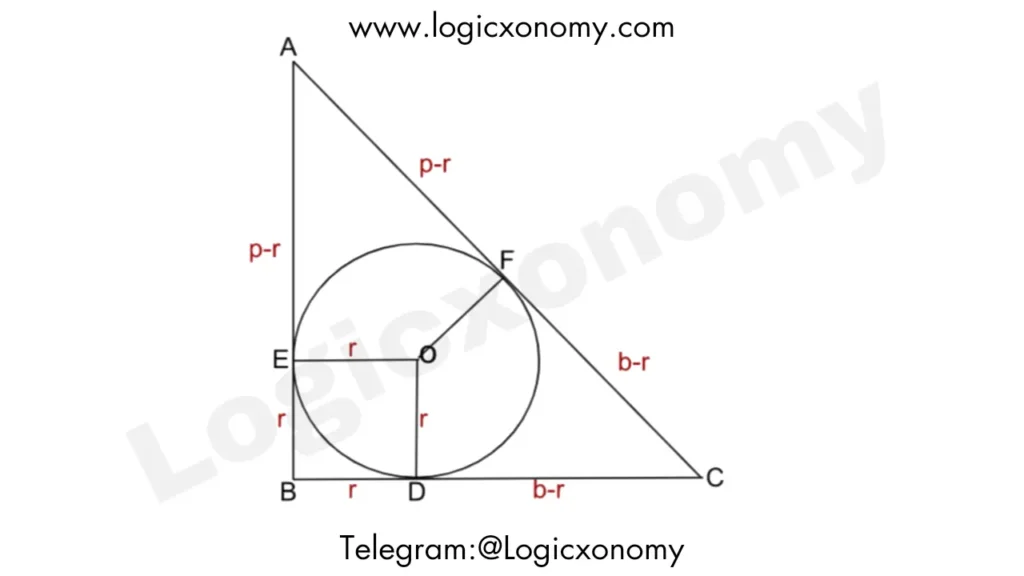
Tangents AF=AE=p-r and CD=CF=b-r

h=p+b-2r

2r=p+b-h ………(iii)

Coordinates of the Incenter

Let the coordinates of the vertices are A(x₁,y₁), B(x₂,y₂), C(x₃,y₃)

Given BD: DC= c:b

So, the coordinates of D(X, Y)= \frac{c.x_3+b.x_2}{c+b},\frac{c.y_3+b.y_2}{c+b}.

AI: ID= b+c: a

So, the coordinates of I= \frac{(b+c).X+a.x_1}{b+c+a},\frac{(b+c).Y+a.y_1}{b+c+a}.

Put values of X and Y (Incenter of a triangle) 

The coordinates of I= \frac{a.x_1+b.x_2+c.x_3}{a+b+c},\frac{a.y_1+b.y_2+c.y_3}{a+b+c}.

Length of the Angle Bisector

In the given figure AB=4 cm, BC=6 cm, CA=3 cm then find the length of Angle bisector AD.

BD: DC= 4:3

BD=4k and DC=3k

BC=7k=6 

k=6/7 cm

BD=24/7 and DC=18/7

Now apply Stewarts formula:

AB²×DC+AC²×BD=BC×(AD²+BD×DC)

4²×18/7+3²×24/7=6×(AD²+24/7×18/7)

Multiply both sides by 7²

4²×18×7+3²×24×7=6×(7²×AD²+24×18)

4²×3×7+3²×4×7=(7²×AD²+24×18)

12×(28+21-36)=7²×AD²

7²×AD²=12×13

7×AD=2√39

AD=1.8 cm (Approx.)

Distance Between Incenter and Vertex

In △AIB, Apply Sine Rule

\frac{AI}{Sin (B/2)}=\frac{AB}{Sin(90°+C/2)}.

AI=c\times\frac{Sin(B/2)}{Cos(C/2)}.

BI=a\times\frac{Sin(C/2)}{Cos(A/2)}.

CI=b\times\frac{Sin(A/2)}{Cos(B/2)}.

AI\times BI\times CI=abc\times\frac{Sin(A/2).Sin(B/2).Sin(C/2)}{Cos(A/2).Cos(B/2).Cos(C/2)}.

Put a=2R×Sin(A)=4R×Sin(A/2)×Cos(A/2)

b=2R×Sin(B)=4R×Sin(B/2)×Cos(B/2)

c=2R×Sin(C)=4R×Sin(C/2)×Cos(C/2)

AI×BI×CI=(4R)³×[Sin(A/2).Sin(B/2).Sin(C/2)]²

Put r=4R.Sin(A/2).Sin(B/2).Sin(C/2)

AI×BI×CI=4Rr² ………….(iv)

Sine and Cosine Formulas

In △BDI, Cot(B/2)= BD/ID=BD/r

BD=r.Cot(B/2)

In △CDI, CD=r.Cot(C/2)

BC=BD+DC

a=r[\frac{Cos(B/2)}{Sin(B/2)}+\frac{Cos(C/2)}{Sin(C/2)}].

a=r[\frac{Sin(\frac{B+C}{2})}{Sin(B/2).Sin(C/2)}].

B+C=180°-A

Sin(\frac{B+C}{2})=Sin(90°-\frac{A}{2})=Cos(A/2).

a=r[\frac{Cos(A/2)}{Sin(B/2).Sin(C/2)}].

a=2R.Sin(A) ……Sine Rule

R is the Circumradius of the triangle

a=2R.2.Sin(A/2).Cos(A/2)=4R.Sin(A/2).Cos(A/2)

Put this value of ‘a’ in the above equation:

r=4R.Sin(A/2).Sin(B/2).Sin(C/2)………..(V)

Cos(A/2)=\sqrt{\frac{s(s-a)}{bc}}.

Cos(B/2)=\sqrt{\frac{s(s-b)}{ca}}.

Cos(C/2)=\sqrt{\frac{s(s-c)}{ab}}.

Cos(A/2).Cos(B/2).Cos(C/2)=\sqrt{\frac{s^2\times \triangle^2}{(abc)^2}}=\frac{s}{\frac{abc}{\triangle}}.

=\frac{s}{4.\frac{abc}{4\triangle}}.

=\frac{s}{4.R}.

s=4R.Cos(A/2).Cos(B/2).Cos(C/2)………..(VI)

Inradius Inequality

The length of the inradius of a triangle is always less than or equal to half the length of the smallest side.

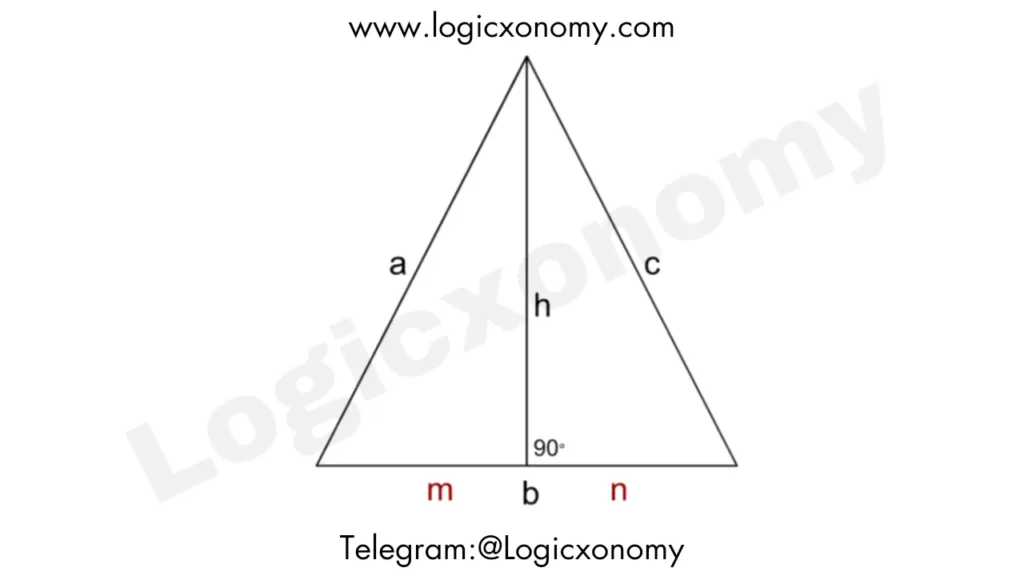
In the given triangle side length ‘b’ is the smallest 

a+m>h

c+n>h

Add both equations: a+c+(m+n)>2h

a+b+c>2h

2s>2h

s>h ……….(i)

Area of the triangle=½×Base×Height

△=½×bh

△=rs

rs=½×bh

h=2rs/b

From equation (i) and (ii)

s>2rs/b

b/2>r

So, the inradius of a triangle is always less than half the length of the smallest side. 

Que 1: In the given △ABC, ID=IE=IF. The side lengths AB=5 cm, BC=6 cm, and CA=8 cm then find the ratio of the areas of △AIG and △ABC.

ar(△AIB): ar(△ABC)= 5: 19

Let, ar(△ABC)=19k

So, ar(△AIB)=5k

ar(△AIG): ar(△BIG)= AG: GB= AC: BC= 4: 3

ar(△AIG)⇒4x

ar(△BIG)⇒3x

ar(△AIB)=ar(△AIG)+ar(△BIG)

5k= 7x

x=5k/7

ar(△AIG)⇒4x=20k/7

ar(△AIG): ar(△ABC)= 20k/7 : 19k

ar(△AIG): ar(△ABC)=20:133