
Two quantities a & b are in the “Golden Ratio”, if (a+b): a =a: b, where a>b>0. It is represented by ‘𝞅‘.
𝞅=(1+√5)/2=1.618033988749….
It is also known as the Divine Proportion and the extreme and mean ratio.
Pentagram: A 5 Point Star, formed from the diagonals of a Regular Pentagon, is called Pentagram or Pentangle.
In the given figure, we have to prove that PS : PR=PR: PQ= PQ: QR= 𝞅=1.618….
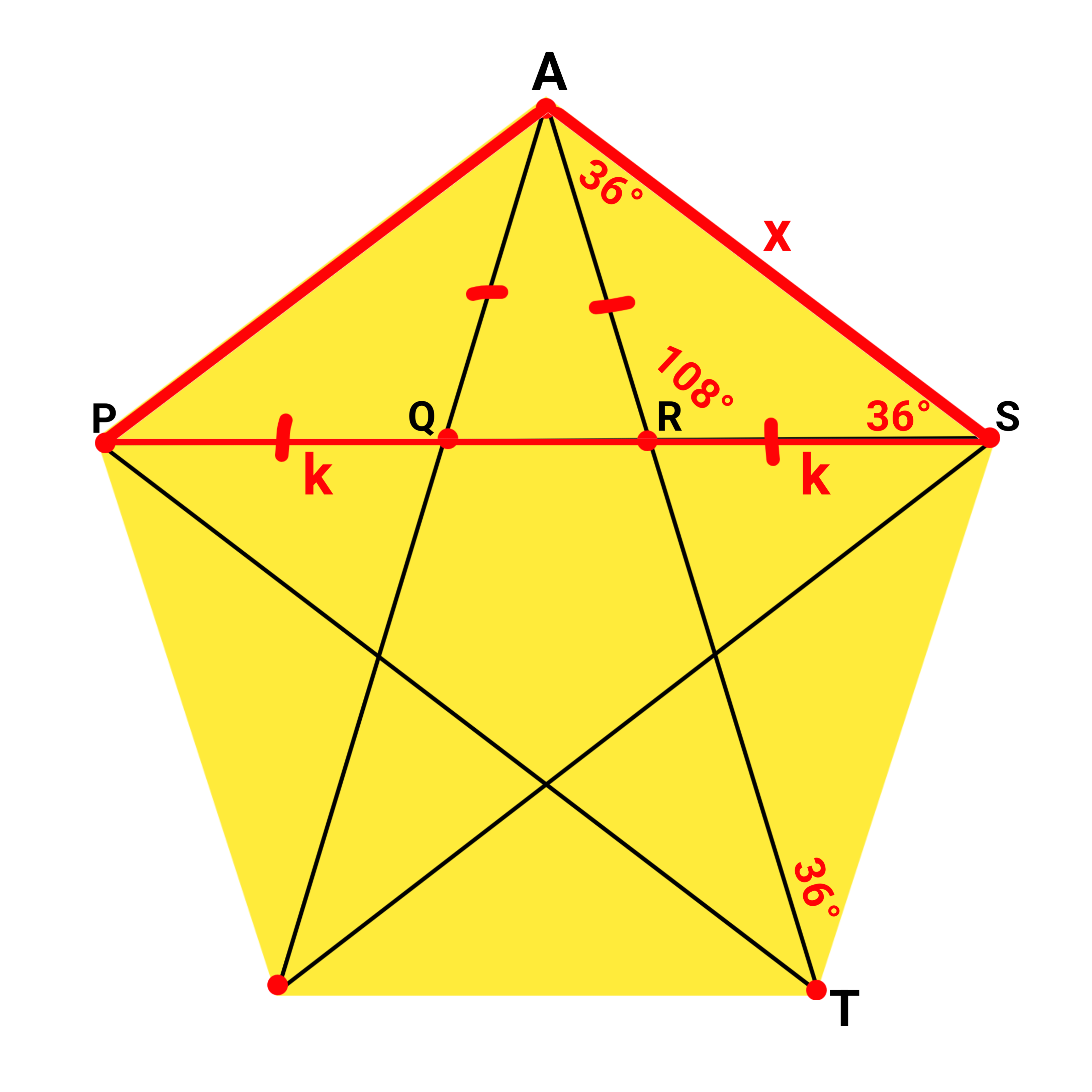
Internal Angle of the Regular Polygon =(n-2)π/n
Where ‘n’ is the number of sides and π=180°
Internal Angle=(5-2)×180°/5=108°
∠PAS=108°
∠APS=∠ASP=36°
In ∆PAS, apply Cosine Formula
PS²=AP²+AS² – 2*AP*AS*Cos(∠PAS)
=x²+x² -2x² Cos(108°)
=2x²{ 1 – (1-√5)/4}
=x²(3+√5)/2
=(6+2√5)x²/4
=(√5+1)²x²/4
PS=(√5+1)/2 ………..(i)

Similarly, Apply the Cosine formula in ∆ARS
k=(√5-1)x/2
PQ=RS=k=(√5-1)x/2
So, QR= PS-2k =(√5+1)/2 -2*(√5-1)/2 =(3-√5)/2
QR=(3-√5)/2
PQ: QR: RS=(√5-1) : (3-√5): (√5-1)
So, PS=(√5-1)+(3-√5)+(√5-1)=√5+1
PR=(√5-1)+(3-√5)=2
PS: PR=(1+√5):2
PR: PQ= 2: (√5-1)=(1+√5):2
PQ: QR=(√5-1) : (3-√5)=(1+√5):2 ……………..{Multiply (3+√5) in numerator and denominator}
Hence Proved…
The Centroid of the Triangle (All Concepts): Click Here

