The centers of a triangle – Incenter, Circumcenter, Centroid, Orthocenter, and Excenter – are fundamental to the study of geometry. Each of these centers has a unique location and set of properties that help define the triangle. In this chapter, we will study each of them one by one.
Incenter
The point of intersection of two or more angle bisectors of a triangle is called the incentre of the triangle. It is denoted by ‘I’, where I is equidistant from all the sides of the triangle. It is the center of the circle that is inscribed inside the triangle and touches all three sides of the triangle.
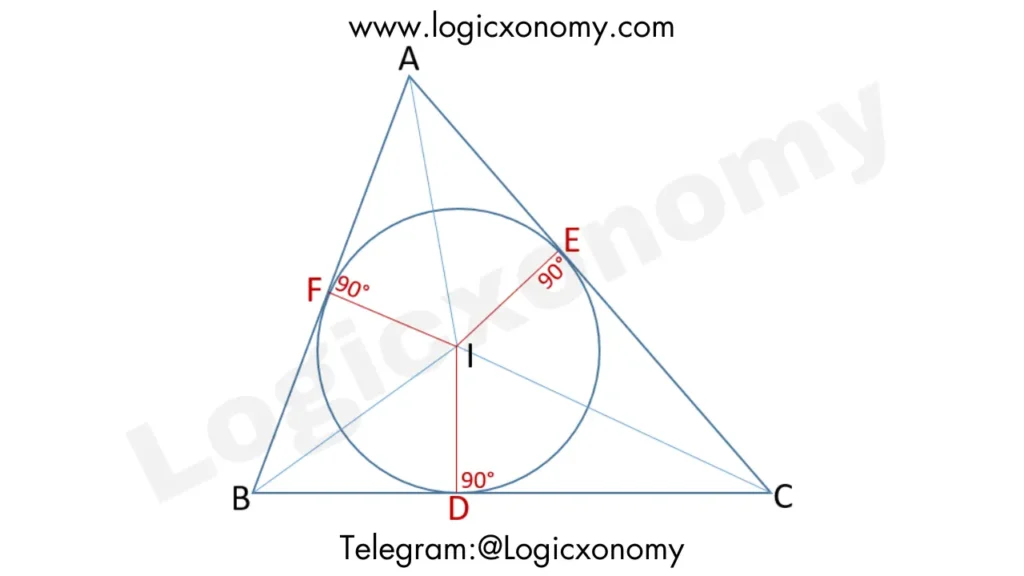
In this given figure: ID=IE=IF=r
Here ‘r’ is the Inradius of the triangle
△=r×s ………(i)
‘s’ is the Semi-Perimeter of the triangle
△ is the Area of the Triangle
Angle Bisector Theorem
The angle bisector drawn from any vertex of a triangle to the opposite side divides that side into segments that are proportional to the adjacent sides of the vertex.
BD: DC=c:b
AE: EC=c:a
BF: FA=a:b
The Incenter of the Triangle (All Theorems with Proof): Click Here
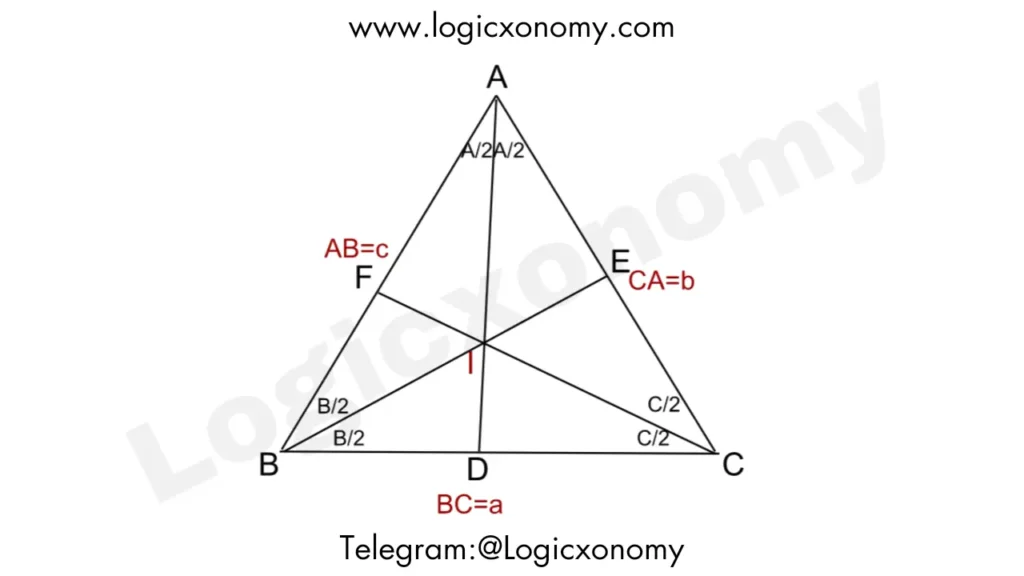
AI: ID=b+c: a
BI: IE=a+c: b
CI: IF=a+b: c

Angle made at the Incenter
∠BIC=90°+A/2
∠CIA=90°+B/2
∠AIB=90°+C/2
It means angles made at the incenter are Obtuse Angles.
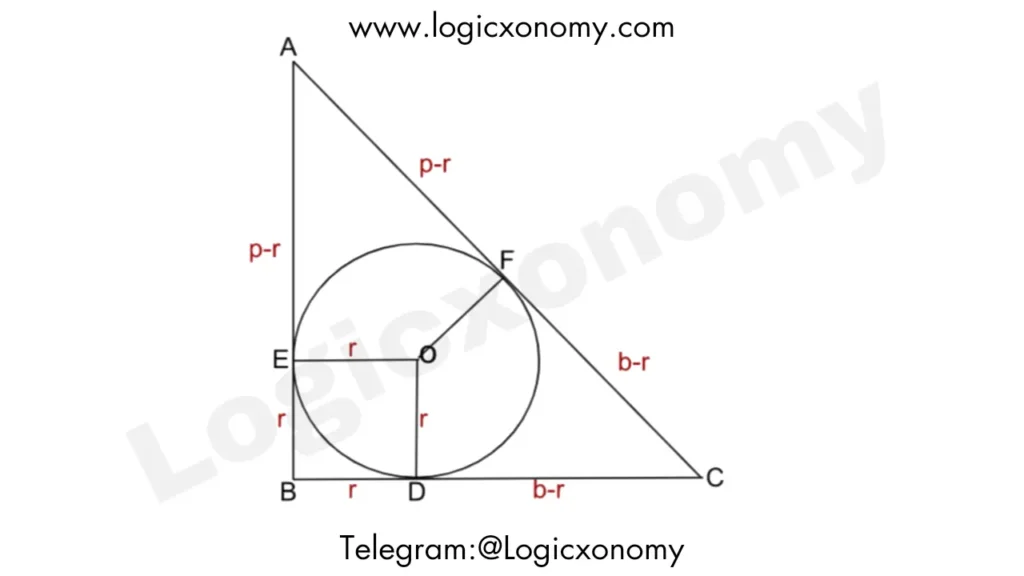
Inradius of the Right Angle Triangle
In △ABC, B=90° and O is the incenter. So altitudes OD=OE=OF=r
AB=p
BC=b
AC=h
Coordinates of the Incenter
Let the coordinates of the vertices are A(x1,y1), B(x2,y2), C(x3,y3)

The coordinates of I= \frac{a.x_1+b.x_2+c.x_3}{a+b+c},\frac{a.y_1+b.y_2+c.y_3}{a+b+c}.
Distance Between Incenter and Vertex
In the above figure, R is the circumradius of the triangle.
R=\frac{abc}{4\triangle}.
AI×BI×CI=4Rr2
Some important results:
r=4R.Sin(A/2).Sin(B/2).Sin(C/2)
s=4R.Cos(A/2).Cos(B/2).Cos(C/2)
Inradius Inequality
The length of the inradius of a triangle is always less than or equal to half the length of the smallest side.
Important Questions
Que 1: In △ABC, sides AB=4 cm, BC=6 cm, CA=3 cm then find the length of Angle bisector AD. Here D is the point on side BC.
Answer: AD=1.8 cm (Approx.)
Que 2: In the △ABC, ID=IE=IF. The side lengths AB=5 cm, BC=6 cm, and CA=8 cm then find the ratio of the areas of △AIG and △ABC. Here Point ‘I’ lies inside the triangle and ID, IE, and IF are the altitudes on the sides BC, CA, and AB respectively. CG is the angle bisector of the triangle where G is on AB.
Answer: ar(△AIG): ar(△ABC)=20:133
Check the detailed blog for the solution: Click Here

